4138

Hybrid O-Space and FRONSAC Imaging

Haifeng Wang¹, Yuchou Chang², and Dong Liang¹

¹Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen, China, ²Department of Computer Science and Technology Engineering, University of Houston-Downtown, Houston, TX, United States

Synopsis

Nonlinear spatial encoding magnetic (SEM) fields can accelerate data acquisitions and improve the imaging quality. In this work, the O-Space and FRONSAC imaging are combined into a hybrid nonlinear spatial encoding approach with dynamic nonlinear gradients. The preliminary experiment of phase mapping shows that the proposed method can be implemented in the current O-Space system. Simulations based on the preliminary experiment demonstrate that this approach can accelerate data acquisitions and reduce artefacts caused by highly undersampling acquisitions.

Introduction

Recently, some schemes of spatial encoding magnetic(SEM) fields ^1-7, have been studied. In terms of speed, O-Space outperforms Cartesian SENSE when the effective acceleration factor approaches, equals, or exceeds the number of radiofrequency (RF) coils used. Based on with the previous works ^3,5, we introduce FRONSAC imaging with dynamic nonlinear gradients ⁶. Here, we describe an imaging approach with O-Space Imaging and FRONSAC dynamic nonlinear gradients that can take a conventional sequences (such as, EPI, Spiral, Rosette or Cartesian) and add a nonlinear Z2-gradient with a low-amplitude sinusoidal oscillation. The linear gradients are applied on the standard linear encoding fields and the sinusoid gradient is only applied on the Z2 encoding field. Images are reconstructed using the Kaczmarz algorithm ⁸. The phase mapping experiment shows that the proposed method can be implemented. Simulations demonstrate this approach can accelerate data acquisitions and reduce undersampling artifacts.

Theory and Methods

It is well known that the potential of the SEMs’ nonlinearity is that they allow the design of inhomogeneous k-space sampling patterns for more efficient acquisitions ⁹. This work is based on the O-Space imaging system ¹⁰ which has Z2 gradients. At the hardware level, this system is controlled by four gradient waveforms $$$g(t) = \begin{bmatrix}g_{x}(t) & g_{y}(t) &g_{z}(t) &g_{z2}(t) \end{bmatrix}^{T}$$$, with three standard linear gradients and one Z2 nonlinear gradient. Because of hardware limitations, the gradients must obey constraints on the maximum gradients and slew rates. Based on the conventional linear gradient waveforms, such as EPI, Spiral, Rosette or Cartesian, we add a low amplitude fast oscillating sinusoidal Z2-gradient waveform to these sequences as shown in Fig. 1. If we define $$$\omega$$$ as the angle rate and $$$A$$$ as the maximum amplitude along Z2 direction, we have $$$g_{z2}(t) = A\cdot sin(\omega\cdot t)$$$. The encoding phase in k-space can be considered as a square which size has timepoint-cycling changes, as seen as Fig. 2. The nonlinear gradient moment serves to spread the sampling function in k-space, such that each data-point reflects a broader weighted sum of k-space points ^9,11. While this sampling scheme is efficient in that it acquires many k-space points at once, it can be difficult to solve for the individual k-space points, potentially leading to other artifacts. The nonlinear gradient moment causes a small variable sized square of local k-space points to be sampled with each data-point. To address hardware feasibility, a sinusoid oscillating Z2 gradient field produced by a head-insert coil was mapped using a phase-mapping sequence as shown in Fig.3 (a), which has additional phase encoding pulses in X and Y before readout and a sinusoidal gradient on the nonlinear SEM channel. The sequence is repeated 4096 times as the phase encoding lobes step through the necessary increments to encode an image (matrix size: 64×64; FOV: 25 cm) for each timepoint in the readout.

Results

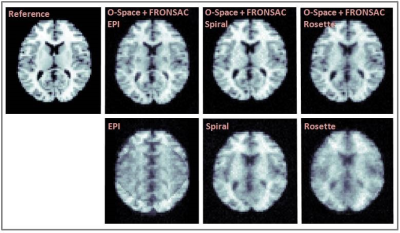
In the phase mapping experiment with the Z2-insert coil, Fig. 3 (b) shows the fits to timecourse in each voxel with the Levenberg-Marquardt nonlinear least squares algorithm ¹², indicating that our current nonlinear gradient coil can achieve an $$$A$$$ of 1400Hz/cm² with an $$$\omega$$$ of 4kHz at the 3T B₀ filed. A significant B₀ eddy current is observed as well, but these frequency shifts do not affect spatial encoding as long as they are known. The data shows that with the current hardware we can produce the sinusoid waveform used for the simulations (matrix size: 64×64) with an acquisition window of 25ms. With these physical limitations in mind we simulated three types of k-space trajectories with the proposed FRONSAC Z2 method, combined with EPI, Spiral and Rosette pulse sequences. This data acquisition window of 25ms would not exceed the mean threshold for peripheral nerve stimulation discomfort (55T/s) over a 25cm field of view. This acquisition scheme would imply a dwell time of approximately 1μs. The maximum slew rate (150mT/m/ms) and gradient amplitudes (40mT/m) along each channel would need to be approximately doubled to achieve the same encodings over these shorter dwell times. All simulations consider Gaussian noises and dephasing. Readout sampled 4096 points, encoding was simulated in MATLAB at a matrix size of 64×64 and white noise was added with amplitude 10% of the mean of the simulated image intensity. For the EPI, Spiral, Rosette, and Cartesian trajectories, $$$\omega$$$ were about 4kHz; $$$A$$$ was 1400Hz/cm2. Fig. 4 shows the proposed method improves image quality in EPI, Spiral, Rosette, and Cartesian acquisitions.

Discussion and Conclusion

The results show the proposed FRONSAC methods also can accelerate data acquisitions and reduce artifacts caused by the conventional imaging using a head-insert O-Space imaging system. In the future, simultaneous multiple-slice images (SMS) ¹³, field distortion effects, and off-resonance effects will be studied.

Acknowledgements

The authors thank Prof. R.Todd Constable and Prof. Gigi Galiana for critical comments, and thank Dr. Leo K. Tam and Dr. Emre Kopanoglu for helpful discussions. Some of the work was supported in part by the National Natural Science Foundation of China (61471350) and the Science and Technology Program of Guangdong (2015A020214019).

References

1. Hennig J, Welz AM, Schultz G, Korvink J, Liu Z, Speck O, Zaitsev M. Parallel imaging in non-bijective, curvilinear magnetic field gradients: a concept study. MAGMA. 2008; 21(1-2): 5-14.

2. Stockmann JP, Ciris PA, Galiana G, Tam LK, Constable RT. O-Space images: highly efficient parallel imaging using second-order nonlinear fields as encoding gradients with no phase encoding. Magn Reson Med. 2010; 64(2): 447-56.

3. Tam LK, Stockmann JP, Galiana G, Constable RT. Null Space Imaging: nonlinear magnetic encoding fields designed complementary to receiver coil sensitivities for improved acceleration in parallel imaging. Magn Reson Med. 2012; 68(4): 1166-75.

4. Gallichan D, Cocosco C, Dewdney A, Schultz G, Welz A, Hennig J, Zaotsev M. Simultaneously driven linear and nonlinear spatial encoding fields in MRI. Magn Reson Med. 2011; 65(3): 702-714.

5. Galiana G, Constable RT. Single Echo MRI. PLoS One. 2014;9(1): e86008.

6. Wang H, Tam LK, Constable RT, Galiana G. Fast rotary nonlinear spatial acquisition (FRONSAC) imaging. Magn Reson Med. 2016 Mar;75(3):1154-65.

7. Galiana G., Luedicke N., Improved Parallel Imaging with Resilience to Gradient Errors. Abstrac: 5163, ISMRM 2017.

8. Kaczmarz S. Approximate Solution for Systems of Linear Equations. International Bulletin of Polish Academy of Science and Letters, 1937; 35: 355–57.

9. Galiana G, Stockmann JP, Tam L, Peters D, Tagare H, Constable RT. The role of nonlinear gradients in parallel imaging: A k-space based analysis. Concepts in Magn Reson Part A. 2012; 40A (5): 256-267.

10. Stockmann JP, Galiana G, Tam L, Juchem C, Nixon TW, Constable RT. In vivo O-Space imaging with a dedicated 12 cm Z2 insert coil on a human 3T scanner using phase map calibration. Magn Reson Med. 2013 Feb;69(2):444-55.

11. Wang H, Tam L, Kopanoglu E, Peters DC, Constable RT, Galiana G. O-space with high resolution readouts outperforms radial imaging. Magn Reson Imaging. 2017 Apr;37: 107-115.

12. Seber GAF, Wild CJ. Nonlinear Regression. Hoboken, NJ: Wiley-InterScience, 2003.

13. Setsompop K, Gagoski BA, Polimeni JR, Witzel T, Wedeen VJ, Wald LL. Blipped-controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g-factor penalty. Magn Reson Med. 2012 May; 67(5):1210-24.

Figures

Fig.1 the timing diagram of a single-shot spiral pulse sequence with the hybrid O-Space and FRONSAC imaging. There is a sinusoidal gradient waveform on the Z2 direction.

Fig.2 the phase gradients for the hybrid O-Space and FRONSAC sequence. The first and second row respectively show the amplitude and phase parts of the spin phase for a timepoint. In every case at different timepoints, the stamp sample a swatch of k-space a point and translates across k-space along the linear trajectory. Meanwhile, the sinusoidal gradients on the nonlinear Z2 channel cause this swatch can change the size.

Fig.3 the phase mapping sequence (a) has a sinusoidal waveform along Z2 and the addition of phase encoding pulses along both X and Y. The results (b) show the amplitudes, and frequencies of each voxel’s phase evolution to calculate the magnitude of the sinusoidal variant nonlinear Z2 field.

Fig.4 the simulation reconstruction results of the conventional linear gradient and hybrid O-Space and FRONSAC methods. Here, a numerical brain phantom is used; SNRs are all 20 dB; image sizes are all 64×64.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)

4138