4137
Model-based Reconstruction with Automatic Scaling for Real-Time Phase-Contrast Flow MRI with Complementary Sets of Radial Spokes1Biomedizinische NMR Forschungs GmbH, Max-Planck-Institute for Biophysical Chemistry, Goettingen, Germany, 2German Center for Cardiovascular Research, partner site Goettingen, Goettingen, Germany, 3Institut für Numerische und Angewandte Mathematik, Goettingen, Germany
Synopsis
Real-time phase-contrast flow MRI is extended from sequential acquisitions of flow-compensated and flow-encoded data with the same set of radial spokes to interleaved acquisitions with different radial spokes oriented by a small Golden angle, thereby improving spatial accuracy and reducing streaking artifacts. To apply model-based reconstructions for this sampling scheme, an automatic scaling of unknowns is proposed, which is capable of balancing partial derivatives and regularizations during the iterative nonlinear inversion.
Purpose
To develop a model-based reconstruction technique with automatic scaling of unknowns for real-time phase-contrast flow MRI acquired via highly undersampled radial FLASH with complementary spokes for flow-compensated and flow-encoded data.Methods
In current real-time phase-contrast flow MRI, both the flow-compensated and flow-encoded data are sequentially acquired via radial spokes with the same k-space encoding1,2. In the model-based reconstruction3, the forward model is formulated as $$$F_{j,l} (x) = U_l \mathcal{F} \{ \rho \cdot e^{i \cdot \Delta \phi \cdot S_l} \cdot c_j \}$$$, where the vector $$$x = (\rho, \Delta \phi, c_1, \cdots, c_N)^T$$$ of unknowns comprises $$$\rho$$$ the proton density, $$$\Delta \phi$$$ the phase difference (i.e. velocity), $$$c_j$$$ the $$$j$$$th coil sensitivity map, and $$$U_l$$$ the sampling pattern of the $$$l$$$th acquisition. The velocity-encoding (Venc) indices $$$S_1 = 0$$$ and $$$S_2 = 1$$$ represent the flow-compensated and flow-encoded acquisition, respectively. The unknowns in this nonlinear signal model are solved by the iteratively regularized Gauss-Newton method with Tikhonov regularization on all unknowns. The balance of partial derivatives and regularizations is achieved by scaling of Venc indices: $$$\hat{S_l} = \frac{\left\lVert M \right\rVert_2}{\left\lVert \Delta \phi \right\rVert_2} \cdot S_l$$$, where $$$M$$$ and $$$\Delta \phi$$$ are approximated by the mean and complex difference of the gridded multi-channel k-space data from the flow-compensated and flow-encoded acquisition, respectively.
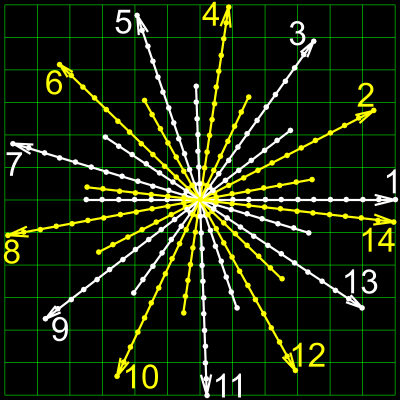
Here, we modify the pulse sequence to allow for complementary sets of spokes. As shown in Figure 1, each pair of flow-compensated and flow-encoded spokes is sampled in an interleaved manner and separated by a constant Golden angle4 of $$$27.19840^o$$$, which is chosen such that the two sets of spokes for one velocity map lead to a nearly uniform coverage of k-space. First, compared to the current sampling scheme1,2, the proposed scheme samples twice more different spokes, thereby effectively reducing the undersampling factor. Second, this sampling scheme enables an additional sliding window reconstruction, which can further increase the frame rate. The main drawback of this sampling scheme, however, is the incompatibility with the previous scaling3, which requires the calculation of the complex difference. As shown in Figure 2, the complex difference between the gridded flow-compensated and flow-encoded k-space sampled with same spokes emphasizes only the flow region (i.e. aorta), while the complex difference from complementary spokes suffers from severe streaks surrounding not only the flow region but also the “static” region (i.e. chest wall). Consequently, the redundant streaks contribute false-positive information to the scaling calculation.
To allow for complementary sets of radial spokes, the model-based reconstruction requires automatic scaling of unknowns, which seeks for the appropriate scaling during iterative reconstructions5. In principle, the scaling of the $$$m$$$th unknown reads as $$$\hat{x}^{(m)} = x^{(m)} \cdot \gamma_m$$$, where $$$\gamma_m$$$ is chosen such that sensitivities of the data with respect to different solution components are balanced, so $$$\gamma_m = \left\lVert DF(x) |_{x^{(m)}} \right\rVert = \left\lVert DF(x) P_m^H \right\rVert$$$ with $$$DF(x)$$$ the derivative of the forward operator and $$$P_m^H$$$ the projection onto the $$$m$$$th unknown. The spectral radius of this matrix norm is determined by its maximal eigenvalue6: $$$\gamma_m = \lambda_0 (P_m DF^H (x) DF(x) P_m^H)^{1/2}$$$, approximated by the power method. In the current implementation, the power method with $$$10$$$ iterations is used only for the odd Newton iterations of each frame.
Experimental implementations of real-time phase-contrast flow MRI use undersampled radial FLASH with the Golden-angle interleaved acquisition scheme. All measurements (TE = $$$1.70$$$ ms, flip angle $$$10^o$$$) had $$$1.5$$$ mm in-plane resolution, $$$320$$$ mm field-of-view, $$$6$$$ mm slice thickness, and $$$35.7$$$ ms ($$$7$$$ spokes, TR = $$$2.55$$$ ms) temporal resolution corresponding to $$$28$$$ frames per second.
Results & Discussion
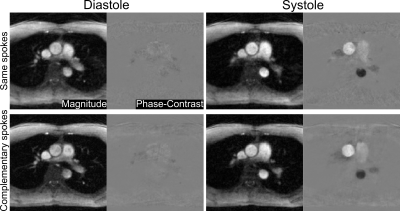
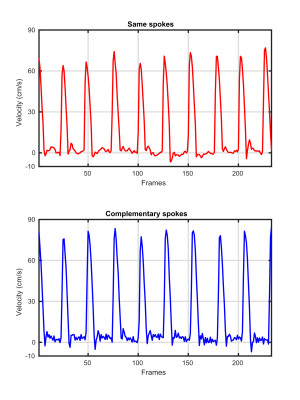
As shown in Figure 3, the automatically scaled model-based reconstruction of complementary sets of spokes yields magnitude images with clearer delineations of small vessels, increased sharpness, and reduced streaking artifacts compared to reconstructions from same sets of spokes. The corresponding phase-contrast velocity maps from complementary sets of spokes tend to be smoother than those from same spokes. Quantitative evaluations of mean velocities spatially averaged over the lumen of the ascending aorta are provided in Figure 4 for both same spokes and complementary spokes. While systolic peak velocities are similar for both acquisition schemes, low velocities during diastole from complementary spokes exhibit more fluctuations than from same spokes.Conclusion
The proposed automatically scaled model-based reconstruction for real-time phase-contrast flow MRI allows for accurate estimates of flow velocities for two different acquisition schemes: same sets of radial spokes and complementary sets of Golden-angle radial spokes for flow-compensated and flow-encoded acquisitions. While velocity maps are of similar quality, complementary spokes substantially improve the spatial accuracy of magnitude images.Acknowledgements
No acknowledgement found.References
1. Joseph A, Kowallick JT, Merboldt KD, et al. Real‐time flow MRI of the aorta at a resolution of 40 msec. J Magn Reson Imaging 2014;40:206-213.
2. Untenberger M, Tan Z, Voit D, et al. Advances in real-time phase-contrast flow MRI using asymmetric radial gradient echoes. Magn Reson Med 2016;75:1901-1908.
3. Tan Z, Roeloffs V, Voit D, et al. Model-based reconstruction for real-time phase-contrast flow MRI: Improved spatiotemporal accuracy. Magn Reson Med 2017;77:1082-1093.
4. Wundrak S, Paul J, Ulrici J, et al. A small surrogate for the golden angle in time-resolved radial MRI based on generalized Fibonacci sequences. IEEE Trans Med Imaging 2015;34:1262-1269.
5. Tan Z, Hohage T, Kalentev O, et al. An eigenvalue approach for the automatic scaling of unknowns in model-based reconstructions: Application to real-time phase-contrast flow MRI. NMR Biomed 2017; doi: 10.1002/mrm.26192.
6. Kress R. Numerical analysis. New York:Springer;1998:38-39.
Figures