4136
Reducing eddy currents in radial cardiovascular MRI using tiny 3D golden-angle1Department of Clinical Physiology, Karolinska Institutet and Karolinska University Hospital, Stockholm, Sweden
Synopsis
Three-dimensional double golden-angle radial imaging has shown great potential in free-breathing whole-heart cardiac cine imaging using data binning, and respiratory resolved cardiac imaging. However, the original golden-angle trajectory involves large jumps in k-space, which leads to eddy current artifacts in bSSFP imaging. For successful binned cardiac imaging, two conditions must be fulfilled; first, the trajectory should provide high k-space uniformity, and second, the trajectory should avoid eddy current induced degradation of image uniformity. The purpose of this work was to develop a double golden-angle radial trajectory that fulfills both of these conditions.
Introduction
Three-dimensional (3D) double golden-angle radial imaging1,2 has shown great potential in free-breathing whole-heart cardiac cine imaging using data binning3, and respiratory resolved cardiac imaging4. The trajectory has been designed by performing successive interval decimations, using two-dimensional golden means5 on a plane which is mapped onto the surface of a sphere2. However, the original golden-angle trajectory involves large jumps in k-space, which leads to eddy current artifacts in bSSFP imaging6, which is the de-facto standard for cardiac imaging. For successful binned cardiac imaging, two conditions must be fulfilled; first, the trajectory should provide high k-space uniformity even after binning, and second, the trajectory should avoid eddy current induced degradation of image uniformity. The purpose of this work was to develop a double golden-angle radial trajectory that fulfills both of these conditions by reducing the jump distance in k-space and at the same time retain the k-space uniformity properties of a golden angle scheme.Methods
By constructing a Fibonacci-like sequence on matrix form and solving for positive and real eigenvalues of the Fibonacci-matrix, the eigenvector $$$v = \begin{pmatrix}0.4656&0.6823&1.0000\end{pmatrix}$$$ was found, where the first two elements are the two-dimensional golden means, $$$\phi_A=0.4656$$$ and $$$\phi_B=0.6823$$$5. In order to reduce the jumps in k-space, we sought to find smaller golden means. By observing that $$$\phi_A = \phi_B^2$$$, a geometric expansion was constructed, such that $$$\phi_n = \phi_0^{n+1}$$$ where $$$\phi_0=\phi_B$$$, and subsequently $$$\phi_1=\phi_A$$$. Each consecutive pair of this generalized golden means geometric series constitutes incrementally smaller steps, still with golden mean properties. The 3D double golden-angle trajectory was originally defined as $$\omega=\cos^{-1}\{m\phi_0\}$$$$\theta = 2\pi\{m\phi_1\}$$where $$$\{\cdot\}$$$ denotes the modulo-1 operation2. However, this causes a discontinuity where the polar angle ω skips from π to 0, which may not be favorable to the eddy current characteristics. Instead, a “soft-modulo” operator, defined as$${\rm{}softmod}\{a,b\}=b-\mid{}a-2b\lfloor{}\frac{a}{2b}\rfloor{}-b\mid$$was used for ω, which replaces the discontinuous modulo function with a triangular wave
k-Space uniformity
The k-space uniformity was assessed in 10 simulated trajectories using the 10 first pairs of generalized golden means, i.e. $$$\langle\phi_0,\phi_1\rangle,~\langle\phi_1,\phi_2\rangle\ldots\langle\phi_9,\phi_{10}\rangle$$$, each trajectory with 900,000 spokes. The trajectories were characterized by the mean angle between consecutive spokes. Each trajectory was binned into 25 cardiac phases and 10 respiratory phases, using electrocardiography and respiratory bellows data from a healthy volunteer. Each of the 250 bins contained approximately 3,600 spokes. The k-space uniformity of each bin was calculated from the standard deviation of Voronoi areas on the binned trajectory surface, and the mean of these 250 standard deviations provided a global k-space uniformity measure for each trajectory design.
Image uniformity
A spherical fluid phantom was imaged using a bSSFP pulse sequence at 1.5 T using the in-bore transmit/receive body coil. Each of the 10 trajectories were repeated 10 times. To avoid systematic errors, the acquisition order was randomized and each acquisition was followed by a 2-minute cool-down period. Image acquisition parameters were; matrix size 128×128×128, voxel size 1.4×1.4×1.4 mm3, TR/TE 2.9/1.4 ms, flip angle 60°, 25,764 spokes. A volume covering 75% of the sphere was used to calculate the normalized absolute average deviation uniformity (NAAD)7. A healthy volunteer was imaged using the trajectory with the best compromise between k-space uniformity and image uniformity. Respiratory self-gating was implemented as a superior-inferior spoke acquired every 25th TR. Parameters that differed from phantom imaging was; matrix size 176×176×176, voxel size 2×2×2 mm3 and 250,000 spokes. Continuous variables were reported as mean±2SD.
Results
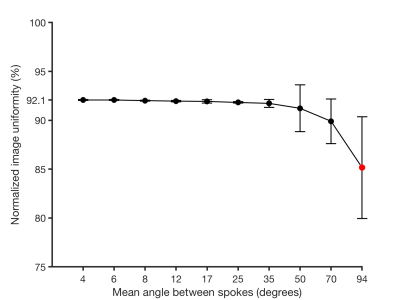
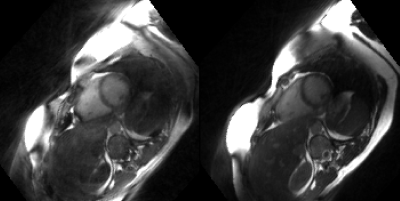
Image uniformity as a function of the mean angle of consecutive spokes is presented in Figure 1. With decreasing mean angles the uniformity converges towards 92.1%. The original double golden-angle trajectory had a uniformity of 85.2±5.2%. Simulation of k-space uniformity is presented in Figure 2 normalized to the ideal uniformity. Figure 3 illustrates the difference in image quality in a healthy volunteer.Discussion
Design of double golden-angle radial trajectories with smaller mean angles between spokes showed improvement in image uniformity, which suggests that the trajectory design reduces eddy currents compared to the original double golden-angle design. Furthermore, lowering the mean angle between spokes affected the binning properties positively with a 4% increase in k-space uniformity at 17° mean angle. It should be noted that the optimal angular increment may vary with the number of spokes and cardiorespiratory bins and more research is warranted. Figure 3 further supports that smaller k-space steps are favorable for reducing eddy current related image artifacts.Conclusion
Generalization of the golden-angle trajectory allowed for smaller angular increments between spokes and provided a best-compromise of 17° with 4% increase in k-space uniformity and a 7% increase in image uniformity.Acknowledgements
No acknowledgement found.References
1. Winkelmann S, Schaeffter T, Koehler T, et. al. An optimal radial profile order based on the golden ratio for time-resolved MRI. IEEE Trans. Med. Imaging. 2007;26(1):68–76.
2. Chan R W, Ramsay E A, Cunningham C H, et. al. Temporal stability of adaptive 3D radial MRI using multidimensional golden means. Magn. Reson. Med. 2009;61(2):354–363.
3. Holst, K, Ugander M, Sigfridsson A. Left ventricular volume measurements with free breathing respiratory self-gated 3-dimensional golden angle radial whole-heart cine imaging – Feasibility and reproducibility. Magn. Reson. Imaging 2017;43:48–55.
4. Holst K, Ugander M, Sigfridsson A. Respiratory variation in left ventricular cardiac function with 3D double golden-angle whole-heart cine imaging. Magn. Reson. Med. Early View. 2017.
5. Anderson P G. Multidimensional Golden Means. Appl. Fibonacci Numbers 1993;5:1–9.
6. Bieri O, Markl M, Scheffler K. Analysis and Compensation of Eddy Currents in Balanced SSFP. Magn. Reson. Med. 2005;137(1):129–137.
7.
NEMA standards publication MS 3-2008 (R2014): Determination
of Image Uniformity in Diagnostic Magnetic Resonance Images. National
Electrical Manufacturers Association 2014:1–19
Figures