4132

In vivo O-space Turbo Spin Echo Imaging with New Reconstruction Algorithm
Nadine Luedicke Dispenza1, Hemant Tagare1,2, R. Todd Constable2,3, and Galiana Gigi2

1Department of Biomedical Engineering, Yale University, New Haven, CT, United States, 2Department of Radiology and Biomedical Imaging, Yale University, New Haven, CT, United States, 3Department of Neurosurgery, Yale University, New Haven, CT, United States

Synopsis

We report the first in-vivo T2 weighted O-space TSE images, and demonstrate that a single TSE dataset can generate T2w images for any of the echo times while still tolerating further undersampling from parallel imaging. In addition to reconstructions based on a refinement of a previously introduced filtering algorithm, we introduce a more general and rigorous reconstruction approach that exploits the geometric relationship between images in the T2w series. The proposed reconstruction algorithm reduces T2 blur and improves contrast agreement to Cartesian TSE images.

Introduction

Acquiring k-space across an echo train reduces scan time but also introduces T2 weighting (T2w) in k-space, which manifests as blur or artifact in the images. In traditional Cartesian TSE, the central region of k-space can be acquired in a narrow range of echo times (1). This yields one T2w image for each scan, though newly introduced methods have extended this to 3D TSE (2). For projection imaging techniques such as O-space imaging, contrast selection is more difficult, but also yields some advantages through the sampling of the central region of k-space with every echo. Special reconstruction techniques are needed to avoid artifacts, and to generate the appropriate T2 weighting at each TE in the echo train from a single scan (3-5). Thus, for a T2w series, O-space TSE effectively provides an additional scan time reduction equal to the length of the echo train. Furthermore, due to the favorable parallel imaging properties of O-space, further acceleration can be achieved. In this work we present the first in-vivo images from O-space TSE data reconstructed with a modification to the T2w filter. In addition, we introduce a new algorithm, similar to the one introduced by Block et al. (5), for O-space TSE, that uses regularization based on the exponential decay, posed as a geometric relationship between the multiple T2w images. Initial results suggest this method substantially reduces blur and improves contrast agreement.

Methods

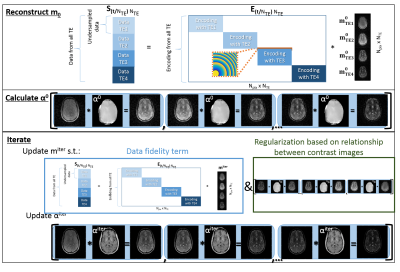
In vivo experiments , using a NLG insert (Tesla Engineering Ltd, Storrington, UK), acquired 256 echoes of 512 points each, with an O-space TSE excitation order previously described (6). TSE imaging parameters were: TR=2000 ms; ETLs of 4 and 8 with echo spacing=18 ms; bandwidth=470 Hz/pixel; slice thickness=5 mm, Z2 strength= 41.6 mT/m2. Image reconstructions were performed using MATLAB (MathWorks Inc, Natick, Massachusetts, USA). Simulated images were generated from noiseless data. Images are reconstructed with a previously described spatial and temporal filter similar to the KWIC filter (4) which depends on the difference between the target TE and the TE at each excitation used during encoding (6). This filter, originally designed to track center placements in an O-space projection imaging scheme, was generalized for arbitrary nonlinear gradient imaging through an explicit model of intravoxel dephasing (7). O-space TSE images are also reconstructed with an algorithm that minimizes: $$ J= ∑_{(n=1)}^{(N_{TE})}‖S_n-A_n m_n ‖^2 +λ∑_{(n=1)}^{(N_{TE}-1)}‖m_{(n+1)}-αm_n ‖ $$ Sn is data acquired at the nth echo time, and mn is the nth image in the T2w image series, which has NTE images. The variable α has the dimensions of a single T2w image. This 2nd term encourages an exponential fit where α(x,y)=exp(ΔTE/T2(x,y)). Conjugate gradient reconstruction of undersampled data at each echo time yields the highly undersampled initial guess for each mn, the m0 seen in Figure 1. The initial map of α is based on a fit of these m0. Subsequently, mn and α are updated according to: $$ m_n^{(iter+1)}=m_n^{iter}- σ_m ( .5 ∇_{m_n } J_1 (m_n^{iter},α^{iter} )+0.5∇_{m_n } J_2 (m_n^{iter},α^{iter} ) ) $$ and $$ α^{(iter+1)}=\frac{∑_{n=1}^{N_{TE}-1}m_{n+1}^{iter} * m_n^{iter})}{∑_{n=1}^{N_{TE}-1} m_n^{{iter}^2} } $$ with the further requirement that: $$$α^{iter+1}=min⁡(max⁡(α^{iter+1},0),1)$$$. After several iterations data from all the TEs is used, which improves undersampling artifacts while also reducing blur from T2 decay.

Results

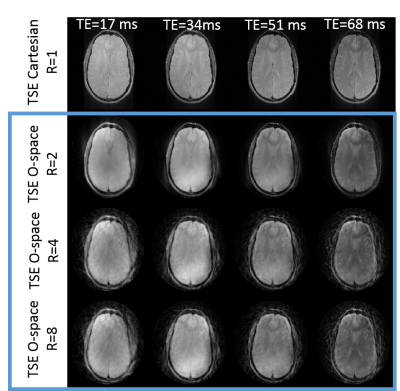
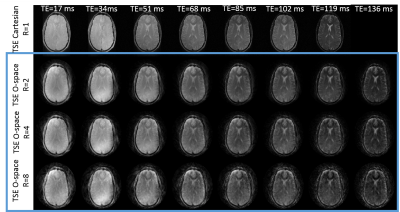
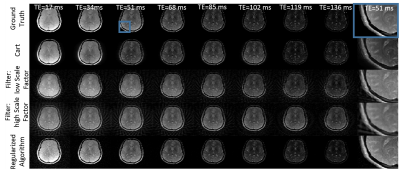
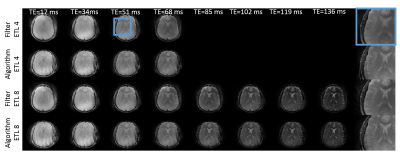
Figures 2 and 3 show in-vivo O-space TSE images acquired with ETLs of 4 and 8 and reconstructed using the filter. The scan time required for the series of T2w images from the O-space dataset is 4 and 8 fold shorter, respectively, than the total scan time required to acquire the Cartesian datasets. Since each TE image is derived using a weighted filter encoding from a mixture of TEs, some residual T2 blur remains. O-space TSE also tolerates further parallel imaging acceleration over conventional TSE. Simulation results in Figure 4 show that the contrast in O-space TSE images reconstructed with the regularized algorithm more closely matches the ground truth and Cartesian contrast than O-space TSE images reconstructed with the filter. Furthermore, unlike the filter, this reconstruction does not require a special excitation order to promote smoothness or a choice of filter parameters, which require some optimization. Since the proposed algorithm equally incorporates the data from all TEs, these images show decreased undersampling artifacts compared to images reconstructed with the filter. Applying this method to experimental in-vivo data, shown in Figure 5, confirms the simulations results.

Conclusion

We have demonstrated that in-vivo O-space TSE allows one to generate multiple T2w contrast images from a single dataset, and the data is compatible with further acceleration from parallel imaging. A regularization based reconstruction algorithm is introduced and applied to O-space TSE, which reduces the blur and artifacts in the O-space TSE images compared to the previously introduced filtered reconstruction.

Acknowledgements

This works was funded by the National Institutes of Health under 5R01EB012289-04, 4R01 EB016978-04, K01EB168977 and R01EB022030. We would like to thank Andrew Dewdney, Keith Heberlein, and Rodney Mick from Siemens for hardware support. We would also like to thank Terry Nixon and Scott McIntyre for support with the Yale nonlinear gradient hardware.

References

1. Constable RT, Anderson AW, Zhong J, Gore JC. Factors influencing contrast in fast spin-echo MR imaging. Magn Reson Imaging 1992;10(4):497-511.

2. Tamir JI, Uecker M, Chen W, Lai P, Alley MT, Vasanawala SS, Lustig M. T2 shuffling: Sharp, multicontrast, volumetric fast spin-echo imaging. Magn Reson Med 2017;77(1):180-195.

3. Galiana G, Peters D, Tam L, Constable RT. Multi-Echo Acquisition of O-Space Data. Magn Reson Med 2014;72(6):1648-1657.

4. Neumann D, Breuer FA, Völker M, Brandt T, Griswold MA, Jakob PM, Blaimer M. Reducing contrast contamination in radial turbo-spin-echo acquisitions by combining a narrow-band KWIC filter with parallel imaging. Magn Reson Med 2014;72(6):1680-1686.

5. Block KT, Uecker M, Frahm J. Model-Based Iterative Reconstruction for Radial Fast Spin-Echo MRI. IEEE Trans Med Imaging 2009;28(11):1759-1769.

6. Wang H, Tam L, Kopanoglu E, Peters D, Constable RT, Galiana G. Experimental O-Space Turbo Spin Echo Imaging. Magn Reson Med 2015;Accepted.

7. Kroboth S, Schleicher KE, Layton KJ, Krafft AJ, Düring K, Jia F, Littin S, Yu H, Hennig J, Bock M, Zaitsev M. Modelling intra-voxel dephasing in MR simulations. In Proceeding of the The 24th Annual Meeting of ISMRM, Singapore, 2016 Abstract 3561 2016.

Figures

Fig. 1 | The reconstruction algorithm first generates undersampled T2 weighted images (m). These images are related via α0. Subsequent iterations incorporate data from all the TEs while regularizing to maintain the relationship between images. A single TSE dataset results in multiple fully sampled T2 weighted images.

Fig. 2 | A single in-vivo Ospace TSE with ETL 4 dataset and multiple Cartesian TSE datasets generate multiple T2 weighted contrast images. However, due to residual T2 weights in k-space, O-space TSE images are penalized by T2 blur. O-space TSE images can be further accelerated by undersampling while maintaining T2 weighted contrast. For O-space images with undersampling factors of 2, 4, and 8 the effective scan time reduction compared to the Cartesian TSE dataset is 8, 16 and 32.

Fig. 3 | In-vivo Ospace TSE with ETL 8 images show that ETL can be increased without incurring further artifacts or blur. Scan time is reduced since only a single O-space TSE dataset must be acquired compared to 8 Cartesian TSE datasets to generate multiple T2 weighted contrast images. Scan time can be further reduced through parallel imaging techniques for effective accelerations of 16, 32, and 64 over Cartesian TSE.

Fig. 4 | Simulation results demonstrate that the O-space TSE image quality from reconstructions with the filter is highly dependent on the filter scale factor. A larger filter scale factor reduces the artifacts but increases T2 blurring. The O-space TSE images reconstructed with the algorithm reduce both blur and artifacts.

Fig. 5 | In vivo images verify simulation results. Images reconstructed with the algorithm exhibit reduced T2 blur and artifacts but appear noisier than images reconstructed with the filter.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
4132