4130

Anisotropic Field-of-Views in 3D Golden Angle Radial Imaging
Guruprasad Krishnamoorthy1,2, Jouke Smink1, Marc Kouwenhoven1, and Marcel Breeuwer1,2

1MR Clinical Science, Philips Healthcare, Best, Netherlands, 2Department of Biomedical Engineering, Eindhoven University of Technology, Eindhoven, Netherlands

Synopsis

3D Golden angle Radial sequence (3D-GArad­) permits reconstruction with varying temporal / spatial resolution from the same dataset. It is less sensitive to motion, flow artifacts and supports ultra-short echo times. It supports self-gated retrospective motion correction techniques. One of the limitations of the current implementations of 3D-GArad is, it only supports isotropic field-of-view (FOV), which leads to redundant sampling and increased scan time when the imaging volume has anisotropic dimensions. In this work, we have developed a method based on the work by Larson et al., to support anisotropic FOV with different FOV-shapes for 3D-GArad.

INTRODUCTION

3D Golden angle Radial sequence (3D-GArad­) permits reconstruction of volumetric data with varying temporal / spatial resolution from the same dataset [1]. It is less sensitive to motion, flow artifacts and supports ultra-short echo times. It supports self-gated retrospective motion correction techniques [2, 3]. One of the limitations of the current implementations of 3D-GArad is, it only supports isotropic field-of-view (FOV), which leads to redundant sampling when the imaging volume has anisotropic dimensions. In this work, we have developed a method based on the work by Larson et al., [4] to support anisotropic FOV with different FOV-shapes for 3D-GArad.

THEORY

In conventional 3D-GArad, the successive azimuthal (Φ) and polar (θ) angles are derived from the eigenvectors of 2D Golden means [1]. This sampling scheme generates a uniform density of radial spokes in azimuthal and polar direction that leads to nearly isotropic FOV for any arbitrary temporal window. When an anisotropic FOV is desired, the revised 3D-GArad sampling scheme should maintain ΔkΦ(Φ) and Δkθ(θ) according to the given FOV dimensions and shape for any arbitrary temporal window, since, ΔkΦ(Φ) = 1 / FOVΦ(θ = π/2,Φ+π/2) and Δkθ(θ) = 1 / FOVθ(θ+π/2,Φ) where ΔkΦ(Φ) and Δkθ(θ) are density of spoke at Φ and θ respectively [4].

METHODS

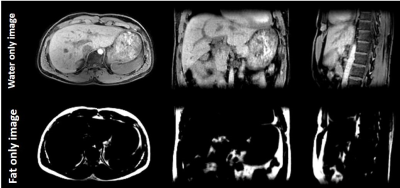
First, fully sampled 2D radial trajectories are computed separately for azimuthal and polar directions using Larson method [4] and noted as Φaniso(n) and θaniso(m) respectively where, n = 0, 2π/N-1, 4π/N-1, 6π/N-1,... 2π, m = 0, π/M-1, 2π/M-1, 3π/M-1,... π, N and M are total number of trajectories computed for azimuthal and polar directions respectively based on the FOV in X,Y and Z dimensions and the desired FOV shape. Then, linear interpolation is done on the fly to compute Φ,θ for the revised 3D-GArad sampling scheme by having Φaniso(n),θaniso(m) as sample points and Φ,θ generated using the conventional 3D-GArad as query points, shown in Figure 1. The developed method was implemented on a 1.5T Philips Ingenia system (Philips Healthcare, Best, Netherlands). Free-breathing abdomen images are acquired using FFE sequence for comparison with the following parameters: TR/TE: 4.8/2.2 ms., 2 mm isotropic resolution. To test the feasibility of free-breathing volumetric fat/water suppression using the proposed 3D-GArad sequence, multi-echo 2-point DIXON (mDIXON) scan was performed with the following parameters: TR/TE1/TE2 = 7.5/4.4/1.85 ms., FOV ratio: 480:260:220 (X:Y:X), 2 mm isotropic resolution, 17711 radial spokes and 2.2 mins. scan time. All dataset were acquired with an identical slab-selective RF excitation (220 mm slab width). 3D gridding was used to reconstruct all images.

RESULTS & DISUCSSIONS

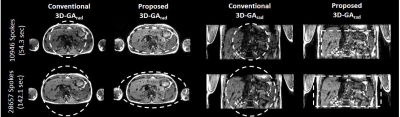
Figure 2 shows the simulation of Point Spread Functions for the conventional 3D-GArad sequence and the proposed 3D-GArad sequence with different FOV-shapes. The same number of radial spokes were used to simulate all the PSFs. The proposed 3D-GArad sequence exhibits noticeably reduced aliasing artifacts compared to the conventional 3D-GArad sequence, shown in Figure 3. This is due to the FOV shape and dimension of the proposed 3D-GArad matched the dimension of the imaging volume (a slab in the abdomen). For the FOV ratio used in the current study (480:260:220), approximately 45% of scan-time reduction can be achieved without increased aliasing artifact compared to the conventional 3D-GArad. More acceleration can be expected with increased FOV asymmetry. In Figure 4, free - breathing volumetric mDIXON scan acquired using the proposed 3D-GArad is shown. Homogenous fat-water separation was achieved using the proposed method.

CONCLUSIONS

We developed a method to support anisotropic field‐of‐view for 3D-GArad and demonstrated the improved scan efficiency compared to the conventional 3D-GArad sequence. This translates to scan-time reduction in many scenarios (cardiac, abdomen, extremities, etc.,) making the proposed 3D-GArad sequence more practical for clinical applications. Further scan time reduction can be achieved when the proposed sequence is combined with acceleration techniques like compressed sensing.

Acknowledgements

This work was supported by the European Commission within the Horizon 2020 Framework through the MSCA-ITN-ETN European Training Networks (project number 642458).

References

1. Chan, R.W., et al., Temporal stability of adaptive 3D radial MRI using multidimensional golden means. Magnetic Resonance in Medicine, 2009. 61(2): p. 354-363.

2. Pang, J., et al., High efficiency coronary MR angiography with nonrigid cardiac motion correction. Magnetic Resonance in Medicine, 2016. 76(5): p. 1345-1353.

3. Holst, K., M. Ugander, and A. Sigfridsson, Left ventricular volume measurements with free breathing respiratory self-gated 3-dimensional golden angle radial whole-heart cine imaging – Feasibility and reproducibility. Magnetic Resonance Imaging, 2017.

4. Larson, P.E.Z., P.T. Gurney, and D.G. Nishimura, Anisotropic Field-of-Views in Radial Imaging. IEEE Transactions on Medical Imaging, 2008. 27(1): p. 47-57.

Figures

Figure 1. Schematic illustration of the method developed to support anisotropic FOV in 3D-GArad. Linear interpolation is done on the fly to modulate the trajectories computed using the conventional 3D-GArad (black) to support anisotropic FOV with different FOV shapes (blue and red). Note the FOV specified here in mm. and isotropic resolution is considered.

Figure 2. Point Spread Functions (PSFs) of a) Conventional 3D-GArad sampling scheme. Proposed 3D-GArad sampling scheme with FOV ratios 100:50:25 (X:Y:Z) with b) Ellipsoidal c) Cylindrical and d) Cuboidal FOV-shape. Blue arrows indicate the separation between the main peak and the aliasing peak.

Figure 3. Comparison of conventional 3D-GArad sequence versus the proposed sequence with cylindrical FOV shape of ratio 480:260:220 (X:Y:Z). The proposed sequence shows significant improvement in the image quality with minimized aliasing artifact compared to the conventional 3D-GArad for the same number of radial spokes. White dotted lines indicate the aliasing free FOV regions. Note that the images are acquired in axial orientation and MPR was performed to reconstruct coronal images.

Figure 4. mDIXON scan acquired using the proposed 3D-GArad sequence with FOV ratio of 480:260:200 (X:Y:Z) with Cylindrical FOV shape and 2 mm isotropic resolution. The images are acquired in axial orientation and MPR was performed to reconstruct coronal and sagittal slices. Note the homogeneous fat-water separation. Residual streaking artifacts are likely due to the breathing motion.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
4130