Synopsis

Computationally intensive image reconstruction algorithms can be made accessible to the diagnostic workflow by streaming data to remote workstations in real-time. Due to bandwidth constraints, data compression is an important tool to ensure that network transmission is not a bottleneck. However, since image quality losses are unacceptable for clinical MRI, it is important to constrain any compression losses below the thermal noise.

Here we propose a framework for online data compression based on constraining SNR loss using a custom-built compression library. Greater than 5-fold data reduction was achieved by accepting a negligible SNR loss.

Introduction

Computationally intensive image reconstruction algorithms are typically implemented offline on high-performance computers or clusters due to limitations of the vendor-provided hardware. Software platforms, such as Gadgetron¹, allow for online reconstruction during clinical MRI exams by streaming data to remote computers or cloud resources in real-time². Given that the MR data acquisition rate can often exceed the available bandwidth at clinical sites, data compression is an important tool to ensure that network transmission is not a bottleneck. However, since image quality losses are unacceptable for clinical MRI, it is also necessary to ensure compression losses are very low – i.e. indistinguishable from thermal noise.

Lossy compression relies on bit-truncation, which effectively adds small, randomly distributed “errors” to a dataset. The key concept for constraining SNR loss is being able to describe the compression error distribution and determine its effect on the reconstructed image.

In this work, we implemented and tested a framework for SNR constrained online data compression using a custom-built compression algorithm.

Methods

Our custom compression algorithm is simple by design, to minimize computation on the local workstation, and to make it statistically intuitive. During compression, each floating-point value in dataset is divided by a common scaling factor, then rounded to the nearest integer. With this approach, the maximum error (ε) between original and compressed values is $$$\pm$$$.5 times the scaling factor, with an equal probability of encountering any error value in between. In this case, the compression error distribution is uniform with a variance of: $$$\sigma_c^2=\frac{(2\epsilon)^2}{12}$$$ .

To limit SNR loss, compression variance is constrained based on the intrinsic noise level, determined from a pre-scan acquisition without RF excitation. Uncorrelated noise variances add linearly, therefore, the signal variance after compression is $$$\sigma_n^2+\sigma_c^2$$$. The noise in the reconstructed image is equal to the noise in the signal because the Fourier transform is a linear operator. This ensures that the image SNR with compression relative to the image SNR without compression is $$$\frac{\sigma_n^2}{\sqrt{\sigma_n^2+\sigma_c^2}}$$$. Using this formula, the scaling factor (2ε) is chosen such that the relative SNR is constrained by a user-defined tolerance. Since noise variances are different among channels of an array, each channel is compressed using a different scaling factor. Compression was tested offline using both simulated data with added noise and phantom MR data (Siemens Aera 1.5T).

Compression was evaluated by measuring image SNR and compression ratios over a tolerance range of 0-10%. Additionally, compression was evaluated online during an in-vivo real-time cardiac cine scan on a healthy volunteer. During MRI acquisition, each readout was compressed on the local host and transmitted to a networked workstation running a Gadgetron reconstruction.

Results

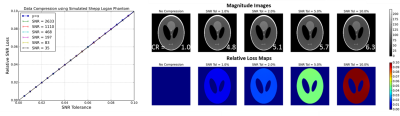
As expected, the relative SNR loss can be controlled using the SNR tolerance input parameter. The relative loss maps show that compression noise is added homogeneously to all image regions with signal, for simulated data where channel noise is uncorrelated. (Figure 1)

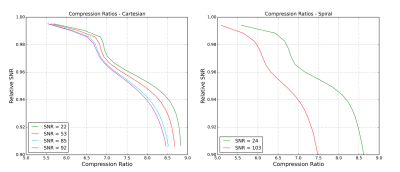
Observed compression ratios varied from approximately 5-9 depending on tolerated SNR loss, acquisition SNR, and acquisition type (figure 2). Relatively high compression ratios can be achieved with almost no loss. Accepting higher losses allows for greater compression ratios, but the returns are diminishing.

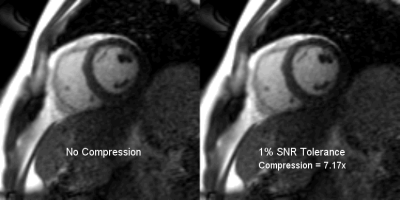
A cine recon of the Gadgetron real-time cardiac scan³ with and without compression is shown in figure 3. In this case, a compression ratio of 7.17 was achieved at 1% tolerance, reducing the required streaming bandwidth from 37 MB/s to 5.2 MB/s (Fast Ethernet = 12.5 MB/s).

Discussion

Conclusion

Acknowledgements

References

1. Hansen MS, Sorensen TS. Gadgetron: an open source framework for medical image reconstruction. Magn Reson Med 2013;69(6):1768-1776.

2. Xue H, Inati S, Sorensen TS, Kellman P, Hansen MS. Distributed MRI reconstruction using Gadgetron-based cloud computing. Magn Reson Med 2015;73(3):1015-1025.

3. Xue H, Kellman P, LaRocca G, Arai AE, Hansen MS. High spatial and temporal resolution retrospective cine cardiovascular magnetic resonance from shortened free breathing real-time acquisitions. Journal of Cardiovascular Magnetic Resonance 2013;15(1):102.