4125

Robust Virtual Coil SAKE with Automatic Rank Thresholding for Removal of EPI Ghost Artifacts
Zhenda Xu1,2, Mengye Lyu1,2, Yilong Liu1,2, Markus Barth3, and Ed X. Wu1,2

1Laboratory of Biomedical Imaging and Signal Processing, The University of Hong Kong, Hong Kong, China, 2Department of Electrical and Electronic Engineering, The University of Hong Kong, Hong Kong, China, 3Centre for Advanced Imaging, The University of Queensland, Brisbane, Australia

Synopsis

Ghost artifacts in EPI can arise from phase error between positive- and negative-echo and inter-shot phase error. Virtual coil SAKE (VC-SAKE) can be used to eliminate these phase errors simultaneously, but its performance relies on selection of parameters. In particular, proper rank thresholding is extremely important. In this study, we proposed to automatically determine the optimal rank threshold by minimizing the image entropy, and evaluated its performance with various datasets from different scanner systems.

Introduction

Ghost artifacts due to phase error between different readout directions and among different shots degrades EPI image quality. They cannot be fully corrected with linear phase correction (LPC) [1], since the phase errors often have 2D and nonlinear components. Virtual coil SAKE (VC-SAKE) was proposed to remove the residual ghost that cannot be fully corrected with LPC [2,3]. Performance of VC-SAKE largely depends on the selection of parameters, more specifically, properly rank thresholding plays a vital role in generating decent results. However, empirically selecting a proper rank threshold is challenging, since the rank is determined by many issues such as object support and coil configuration, etc. Noting that appearance of residual ghost results in increasing of image entropy, and it has already been used to determine the linear phase parameters for LPC. In this study, we utilize image entropy to achieve automatic rank thresholding.

Methods

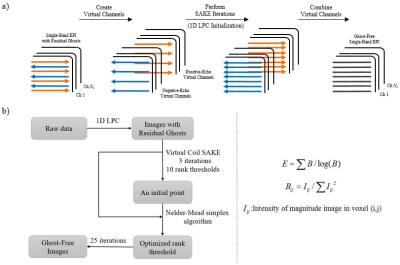
Proposed method: Figure. 1a revisits the basic workflow of VC-SAKE, which consists of three steps: virtual channel creation, SAKE iteration, and virtual channel combination. Figure. 1b illustrates the proposed method for automatic rank thresholding using VC-SAKE based on entropy minimization.

First, Nyquist ghosts are partially removed by 1D linear phase correction (LPC) based on entropy minimization [1].

Then, VC-SAKE is applied to eliminate the residual Nyquist ghosts using a small number of iterations (<3) and 10 rank thresholds. The rank threshold that achieves minimum image entropy is selected as initial point (the rank threshold corresponding to the smallest entropy).

After that, Nelder-Mead simplex algorithm [4] is used to find the optimal rank threshold with the step size set to 5%. In our implementation, 3 SAKE iterations were performed with kernel size=6×6, window-normalized rank threshold ranging from 0 to 5 (equivalent to rank = 0~180 without window-normalization). Finally, to evaluate the feasibility of this method, VC-SAKE with 25 iterations was performed using the automatically determined rank threshold to generate the final reconstruction.

Experiments

Phantom and human brain imaging at large-bore 7T system

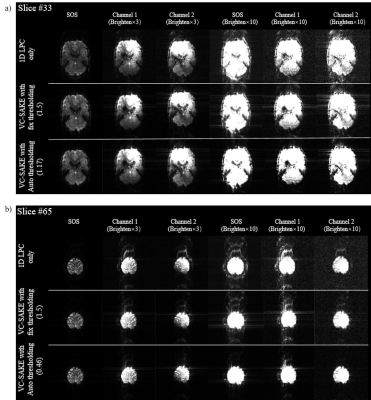
Phantom and human brain data were collected on a 7T Siemens whole-body research scanner equipped with a 32-channel head coil. At MB=2, TE/TR=30/21670ms, flip angle=70°, matrix size=128×128, slice number=80, slice thickness=2mm.

Oblique view at small-bore 7T system

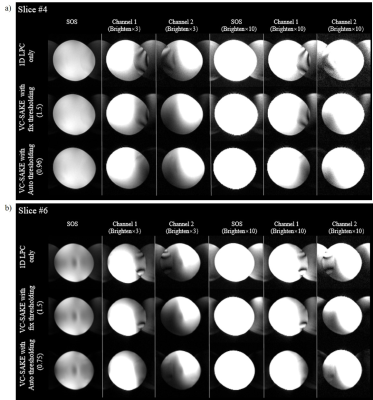
Experiments were performed at 7T (Bruker) equipped with a 4-channel surface head coil. The acquisition parameters are TE/TR=25/2000ms, flip angle=90˚, FOV=50×50mm2, matrix size=128×128, echo-spacing=0.32ms, slice number=6, slice thickness=2mm.

Rat brain imaging at small-bore 7T system

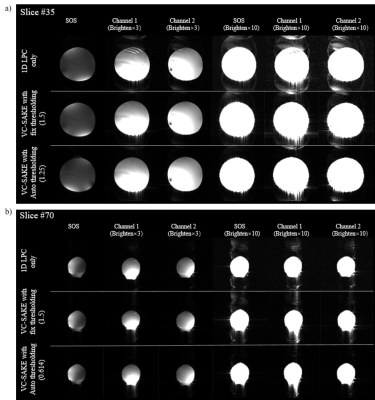
Experiments were performed at 7T (Bruker) using a 4-channel surface coil. The in vivo rat brain was imaged with parameters TE/TR=16/2000 ms, flip angle=90˚, slice thickness=1mm, FOV=40×40 mm2, and matrix size=96×96.

Results

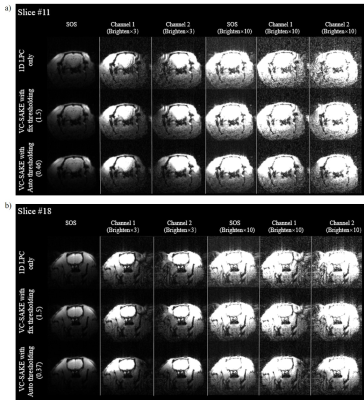
Figure 2-5 show the imaging result in different scenarios. With 1D LPC correction, the reconstructed image still have severe ghosts. If VC-SAKE is performed with fixed thresholding, its performance varies across different slices or with different scanning systems. With improper thresholding, the final images still have distinct artifacts. With automatic thresholding, VC-SAKE have decent performance in all these scenarios, generating images with least ghost level.

Discussion and Conclusion

The proposed method have been evaluated with varieties of datasets from our on-going projects, results showed its robustness in finding the optimal rank in different scenarios. The proposed method can efficiently find the optimal rank threshold for image slices from different scanner systems, or with different spatial support. This method can be generally adapted to other low rank based ghost correction methods such as LORAKS [5] and ALOHA [6]. Future studies can further investigate the possibility of automatic determination of kernel sizes and iteration numbers.

Acknowledgements

This work was supported by the Hong Kong Research Grant Council (Grants C7048-16G and HKU17103015 to E.X.W.).

References

[1] Skare, S., Clayton, D. B., et al., ISMRM, 2006.

[2] Lyu, M., Barth, M., et al., ISMRM, 2017.

[3] Peter, J. Shin., Peder, E. Z. Larson., et al., Magn Reson Med, 2014. 72: p. 959-70.

[4] Lagarias, J. C. et al., SIAM Journal of Optimization, 1998. 9(1): p. 112–47.

[5] Lobos, RA., Kim, TH. et al., ISMRM, 2017.

[6] Lee, J., Jin, K. H., et al., Magn Reson Med, 2016. 76(6): p. 1775-89.

Figures

Figure 1. a) The diagram of VC-SAKE: first, the input k-space data are organized into positive- and negative-echo virtual channels, then missing data points in all virtual channels are initialized with 1D LPC results, then jointly updated in SAKE iterations. Finally, the positive- and negative-echo virtual channels are combined to generate the final images. b) The flowchart of the proposed method. A small number of iterations (<3) and 10 rank thresholds is used to find an initial point that achieves minimum image entropy. Then, Nelder-Mead simplex algorithm is employed to further optimize the rank threshold.

Figure 2. Representative slices in 7T human brain data with different rank thresholds. Sum-Of-Square (SOS) images and images from selected channels are displayed in normal and enhanced brightness. Noting that the object in Slice #65 is much smaller than in Slice #33, and the automatically obtained threshold in Slice #65 (0.46) is much lower than that in Slice #33 (1.17). With improper rank thresholding, the reconstructed images have visible residual artifacts, whereas the proposed automatic thresholding lead to robust high-quality ghost removal.

Figure 3. Representative slices in 7T oblique single shot data with different rank thresholds. Sum-Of-Square (SOS) images and images from selected channels are displayed in normal and enhanced brightness. Noting that the object in Slice #6 has similar size to Slice #3, and the automatically obtained threshold in Slice #6 (0.75) is close to that in Slice #4 (0.96). With improper rank thresholding, the reconstructed images have visible residual artifacts, whereas the proposed automatic thresholding lead to robust high-quality ghost removal.

Figure 4. Representative slices in 7T phantom 2 shot data with different rank thresholds. Sum-Of-Square (SOS) images and images from selected channels are displayed in normal and enhanced brightness. With improper rank thresholding, the reconstructed images have visible residual artifacts, whereas the proposed automatic thresholding lead to robust high-quality ghost removal.

Figure 5. Representative slices in 7T rat single shot data with different rank thresholds. Sum-Of-Square (SOS) images and images from selected channels are displayed in normal and enhanced brightness. With improper rank thresholding, the reconstructed images have visible residual artifacts, whereas the proposed automatic thresholding lead to robust high-quality ghost removal.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
4125