4120
Correction of Slice-Specific Nyquist Ghost Artifact for Simultaneous Multi-Slice EPI1Department of Radiologic Technology, Chiang Mai University, Chiang Mai, Thailand, 2Department of Biomedical Magnetic Resonance, Otto von Guericke University Magdeburg, Magdeburg, Germany
Synopsis
The slice-specific ghosting artifact has been challenging for SMS-EPI. A standard 1D-based phase correction usually leads to increased residual ghosting artifacts in case of subject motion or eddy current variations at different time points. In this study, we propose a dynamic 2D slice-specific phase correction to address the slice-specific phase error. This correction scheme does not require additional time for acquiring 2D phase difference scans. It is a combination between slice-GRAPPA and model-based framework. The result shows that the ghost-to-signal ratios for MB3Ry2 in human brain obtained by the proposed and vendor-provided reconstruction were 1.37% and 2.66%, respectively.
PURPOSE
To develop the reconstruction pipeline that intrinsically accounts for both simultaneous multi-slice echo planar imaging (SMS-EPI) reconstruction and slice-specific Nyquist ghosting correction.INTRODUCTION
The slice-specific ghosting artifact has been
challenging for SMS-EPI. A 1D non-phase-encoded single slice navigator
(1D-SB-Nav) acquired once prior to the SMS-EPI time series is usually employed
to handle the phase error in dynamic multiband (MB) data1-3.
However, 1D-based phase correction may lead to increased residual ghosting
artifacts in case of subject motion or eddy current variations at different
time points4. Such artifacts can be suppressed more effectively by 2D correction, but at the cost of an additional full k-space
reference scan to obtain such 2D phase information. In this study, we propose a dynamic 2D slice-specific
phase correction to address the slice-specific phase error. This correction
scheme does not require additional time for acquiring 2D phase difference
scans.METHOD
Data Acquisition: SMS-EPI data sets were acquired on a 3T MR (80 mT/m gradients) (Prisma, Siemens Healthcare, Erlangen, Germany) using a 64-channel head/neck coil. The healthy volunteer was scanned with informed consents according to the IRB-approved protocol. All scans were performed using a 2D blipped CAIPI multiband EPI sequence from the Center for Magnetic Resonance Research, University of Minnesota. In this study, SMS-EPI with multiband factor 2 (MB2), in-plane acceleration factor two (Ry2) was investigated. For fMRI study, the entire brain was covered using 78 slices with 1.5 mm isotropic resolution with 180 measurements. A standard four-finger tapping task was performed.
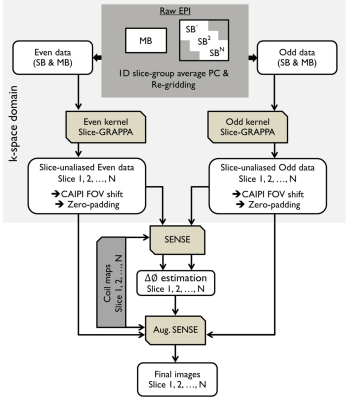
Reconstruction: Figure 1 depicts the proposed reconstruction pipeline which was performed offline using MATLAB software. The slice-GRAPPA5 was employed to handle the slice aliasing problem. For in-plane reconstruction,the model-based framework6 with a single forward operator ($$${A}$$$) (so-called augmented SENSE) that includes both echoes and phase errors was employed. The artifact-free EPI ($$$v$$$) was solved by using the CG method:
$$min_{v}{‖s-A(v)‖_2^2+λ‖Lv‖_2^2 }, with A=∑_{k=1}^{2}∑_{j=1}^{N_c}M^k FC^j ∅^k ----- [1]$$
where $$$∅^{k}$$$ consists of a set of phase information {$$$e^{i0}$$$ for $$$k=1$$$, and $$$e^{i∆φ}$$$ for $$$k=2$$$}. $$$M$$$ is the sampling mask (1=sampled, 0=otherwise), where $$$k=1$$$ is for the even echo and $$$k=2$$$ is for the odd echo. $$$F$$$ denotes the discrete Fourier transform and $$$L$$$ is regularization matrix. The regularization parameter ($$$λ$$$) is a positive real number. Coil sensitivity $$$C^{j}$$$ of channel $$$j$$$ was calculated from FLASH-ACS data.
RESULTS
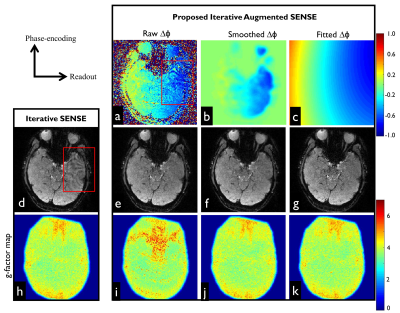
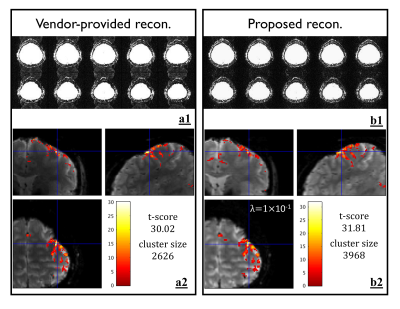
Figure 2d shows that the images obtained by the standard SENSE appear suboptimal and residual artifacts are clearly visible particularly in regions with local field inhomogeneity as highlighted by the red boxes. The phase corresponding to the residual artifact is illustrated in Figure 2a. After accounting 2D residual phase errors into augmented SENSE, the artifacts were successfully suppressed, as shown in Figure 2e-2g. Due to ill-conditioning problem of the raw phase map obtained from effectively double-undersampled images (even and odd), noise amplification propagated into the final reconstructed image, resulting in high g-factor values (Figure 2i). This problem could be mitigated when either the smoothed (Figure 2j) or polynomial fitted (Figure 2k) phase maps were used. Figure 3a1 shows that the ghosting levels on the vendor-provided reconstruction images were clearly visible, but largely suppressed by the proposed scheme (Figure 3b1). In Figure 3a2 and 3b2, the highest t-score value obtained from the vendor-provided data was 30.02, whereas such value obtained from the proposed data was increased 5.96%. Although, the λ value of 0.1 resulted in the smoothed images, the activation map appears only slightly spread out.DISCUSSION
Incomplete phase correction resulted in residual artifacts as illustrated in Figure 2d. This example shows that 1D phase correction is likely to be inadequate. The improved results obtained by the proposed reconstruction warrant 2D slice-specific phase correction. In this work, the 2D-self phase map correction provided images with relative lower Nyquist ghost compared to the standard 1D approach. Although the proposed phase maps are corrupted by g-factor noise amplification, the smooth 2D phase maps obtained by either polynomial fitting or filtering can be used to address this issue as indicated by g-factor maps in Figure 2j and 2k. In general, the smoothing and/or fitting techniques generally remove high spatial frequency components, resulting in residual phase errors particularly in high susceptibility regions where high-order phase variations are present. In such cases, two frames of calibration data with equal but opposite polarity readout gradients, known as the GESTE method7, may be able to provide high quality 2D phase maps. Since these maps are obtained from fully sampled k-space data, fitting or smoothing methods may be not required. Consequently, all phase information is maintained and could be used to correct high-order phase errors.Acknowledgements
This study was supported by the German Research Foundation DFG (SP632-4) and the National Institutes of Health (R01-DA021146). We greatly appreciate all support from the biomedical magnetic resonance (BMMR) team members. U. Yarach thanks the faculty of Associated Medical Sciences, Chiang Mai University, Thailand for financial support.References
1. Setsompop K, Cohen-Adad J, Gagoski BA, Raij T, Yendiki A, Keil B, Wedeen VJ, Wald LL. Improving diffusion MRI using simultaneous multi-slice echo planar imaging. Neuroimage 2012; 63(1): 569-580.
2. Zhu K, Dougherty RF, Wu H, Middione MJ, Takahashi AM, Zhang T, Pauly JM, Kerr AB. Hybrid-Space SENSE Reconstruction for Simultaneous Multi-Slice MRI. IEEE Trans Med Imaging 2016; 35(8): 1824-1836.
3. Koopmans PJ. Two-dimensional-NGC-SENSE-GRAPPA for fast, ghosting-robust reconstruction of in-plane and slice-accelerated blipped-CAIPI echo planar imaging. Magn Reson Med 2017; 77(3): 998-1009.
4. Zaitsev M, Akin B, LeVan P, Knowles BR. Prospective motion correction in functional MRI. Neuroimage 2017; 154: 33-42.
5. Setsompop K, Gagoski BA, Polimeni JR, Witzel T, Wedeen VJ, Wald LL. Blipped-controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g-factor penalty. Magn Reson Med 2012; 67(5): 1210-1224.
6. Yarach U, In MH, Chatnuntawech I, Bilgic B, Godenschweger F, Mattern H, Sciarra A, Speck O. Model-based iterative reconstruction for single-shot EPI at 7T. Magn Reson Med 2017; doi: 10.1002/mrm.26633
7. Hoge WS, Polimeni JR. Dual-polarity GRAPPA for simultaneous reconstruction and ghost correction of echo planar imaging data. Magn Reson Med 2016; 76(1): 32-44.
Figures