4119
3D Motion Estimation and Correction of Motion in Sequential Slices of Kidney Diffusion-Weighted MRI1Boston Children's Hospital and Harvard Medical School, Boston, MA, United States
Synopsis
In this paper we introduced a motion-compensated model estimation technique for renal DW-MRI. The technique has two main components: 1) we adapted an approach based on robust state estimation, which was recently utilized to solve slice-based motion estimation, to track physiological motion (including respiratory motion); 2) we used weighted least squares to estimate diffusion tensor model and calculate diffusion parameters from motion-compensated data. Overall, our method achieved the highest FA values in the medulla, compared to no motion correction and volume to volume registration which resulted in reduced FA values, artifacts, and blurrier FA, MD and AD maps.
Introduction
Quantitative diffusion-weighted MRI (DW-MRI) parameters have been suggested as useful markers in evaluating renal function1. Accurate model fitting and estimation of diffusion parameters is limited by respiratory, cardiac and bulk motion. Recent studies demonstrate the impact of motion compensation; however, current motion compensation techniques either require a complex setup (breathholding, external devices), increase scan time (triggering, respiratory gating), or cannot fully correct for the effect of motion (e.g., gating, and 3D volumetric registration, or 2D slice-based registration). In this work we propose a motion-robust parameter estimation technique for kidney diffusion-weighted MRI is based on robust state estimation2 for dynamic motion modeling, and 3D slice-to-volume image registration, which has been used in several challenging body imaging applications3-5.
Methods
We propose to track and estimate physiological motion (including respiratory motion) based on the information content of the sequential DW-MRI slice acquisitions. In standard body diffusion imaging, each slice takes around 150-200ms to acquire. This high sampling rate in renal DW-MRI allows effective estimation of physiological motion via a slice registration algorithm adapted from6. The estimated motion parameters are then applied to correct the position of each slice in 3D, which leads to scattered point cloud data, that is used in weighted least squares estimation of diffusion tensor model parameters. For sequential slice registration-based motion tracking, the first b=0s/mm2 (B0) image is used as the initial reference volume. Then, an average B0 image is reconstructed after one iteration of slice motion correction. This averaged B0 image is used as reference to register next set of b values, i.e. b=10s/mm2 images, followed by reconstruction of an average diffusion-sensitized image (B10) from b=10s/mm2 images. The output (B10) image is used as the reference for the reconstruction of the next set of b value images, and the process repeats for all b-values; in this case finishing at b=800s/mm2. At the end, we have reconstructed average reference images for all the b values, which were used as reference images to estimate motion parameters for all DW-MRI slices over time using the proposed sequential slice registration technique.
To test our technique, we imaged 6 healthy volunteers. Kidney DW-MRI involved free-breathing single-shot echo-planar imaging using the following parameters: repetition/echo time (TR/TE)=3300/91ms; matrix size=158×118; field of view=360×270 mm; slice thickness/gap = 4 mm/0 mm; 16 coronal slices; 10 b-values = 0, 10, 30, 80, 120, 200, 400, 600, 800 s/mm2, 17 gradient directions; 10 b = 0 images; total acquisition time=10.7 minutes. This protocol allowed sequential acquisition of N = 16 × 9 × 17 + 16 × 10 × 1 = 2608 DW-MRI slices.
Results
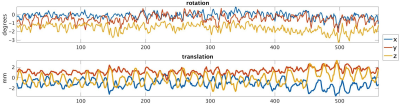
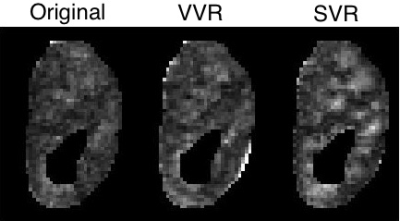
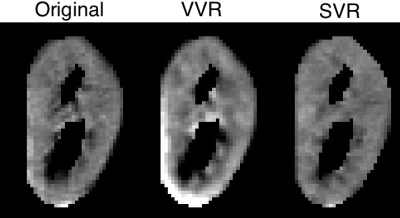
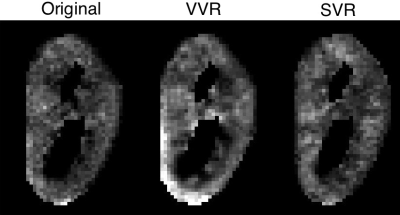
Using the proposed motion estimation technique, we measured three rotation and three translation parameters of each slice. Figure 1 shows the motion parameters calculated by the motion tracking algorithm plotted against time in seconds for one of the subjects. It is observed that the registration-based motion tracking algorithm accurately estimated large respiratory motion in z: head-to-foot, with smaller periodic motion in x and y, while found very small translational motion in the left-to-right direction. The magnitude and frequency of the translation was consistent with the expected respiratory motion. We compared the fractional anisotropy (FA) maps and values obtained from diffusion tensor models computed using a) w/o registration, b) vol-to-vol registration (VVR), and c) our method that uses slice-to-vol registration (SVR). Figure 2 shows the FA maps in one of the kidneys from one of the subjects, and Figure 3 and 4 shows the mean diffusivity (MD) and axial diffusivity (AD) for the same subject. Table 1 reports and compares mean FA values in the medulla and cortex for the three methods. Overall, our method achieved the highest FA values in the medulla, while the other two methods resulted in reduced FA values, artifacts, and blurrier FA, MD and AD maps.Discussion and Conclusion
In this paper we introduced a motion-compensated model estimation technique in renal DW-MRI. The technique has two main components: 1) we adapted an approach based on robust state estimation1, which was recently utilized to solve slice-based motion estimation6, to track physiological motion (including respiratory motion); 2) we used weighted least squares to estimate diffusion tensor model and calculate diffusion parameters from motion-compensated data. Our motion-compensated DW-MRI framework can also be used with other signal decay models of kidneys such as combined diffusion tensor-IVIM model7 or 3-compartment signal decay model8.Acknowledgements
This work was supported in part by a Career Development Award from the Crohn's and Colitis Foundation and in part by the National Institutes of Health (NIH) grants R01 DK100404, R01 EB018988, and R01 EB019483References
1) Eisenberger, U., Binser, T., Thoeny, H.C., Boesch, C., Frey, e.a.: Living renal allograft transplantation: diffusion-weighted MR imaging in longitudinal follow-up of the donated and the remaining kidney. Radiology 270(3), 800–808 (2013)
2) Agamennoni, G., Nieto, J.I., Nebot, E.M.: Approximate inference in state-space models with heavy-tailed noise. IEEE Transactions on Signal Processing 60(10), 5024–5037 (2012)
3) Fei, B., Duerk, J.L., Boll, D.T., et al.: Slice-to-volume registration and its poten- tial application to interventional MRI-guided radio-frequency thermal ablation of prostate cancer. IEEE Transactions on Medical Imaging 22(4), 515–525 (2003)
4) Ferrante, E., Paragios, N.: Slice-to-volume medical image registration: A survey. Medical Image Analysis 39, 101–123 (2017)
5) Gholipour, A., Estroff, J.A., Warfield, S.K.: Robust super-resolution volume recon struction from slice acquisitions: application to fetal brain MRI. IEEE Transactions on Medical Imaging 29(10), 1739–1758 (2010)
6) Marami, B., Scherrer, B., Afacan, O., Erem, B., Warfield, S.K., Gholipour, A.:Motion-robust diffusion-weighted brain MRI reconstruction through slice-level registration-based motion tracking. IEEE Transactions on Medical Imaging 35(10), 2258–2269 (2016)
7) Notohamiprodjo, M., Chandarana, H., et al.: Combined intravoxel incoherent motion and diffusion tensor imaging of renal diffusion and flow anisotropy. Magnetic Resonance in Medicine 73(4) (2014)
8) Van Baalen, S., Leemans, A., Dik, P., Lilien, M.R., Ten Haken, B., Froeling, M.: Intravoxel incoherent motion modeling in the kidneys: Comparison of mono-, bi-and triexponential fit. J. of Magnetic Resonance Imaging 46(1), 228–239 (2017)
Figures