4118
An alternating algorithm for dynamic cardiac MRI reconstruction and motion estimation1University of California, Los Angeles, Los Angeles, CA, United States
Synopsis
This work deals with the problem of dynamic MRI reconstruction and motion estimation jointly. Specifically, a multi-scale affine optical flow model is incorporated into the compressed sensing framework. Simulation results demonstrate the efficiency of the proposed algorithm in image reconstruction and motion estimation against the standard CS based method for MRI reconstruction.
Introduction
Dynamic MRI (DMRI) reconstruction aims at obtaining spatial-temporal MRI sequences from the measurements in the k-t space. A well- known challenge in DMRI reconstruction is the trade-off between spatial and temporal resolution due to the limited image acquisition speed. This is particularly important in applications where motion needs to be quantified. To overcome the challenges, DMRI reconstruction and motion estimation have been jointly explored. In this work, we incorporate the multi-scale optical flow (OF) model into the compressed sensing (CS) framework to jointly reconstruct the DMRI and estimate the motion vectors. Moreover, in order to model the typical cardiac motion, such as rotation, expansion, contraction and shear, an local affine velocity model is considered for the motion vectors. The formulated optimization problem is then solved with an alternating algorithm.Method
Given the DMRI in a matrix form, where each column represents a temporal frame of the DMRI, the problem of DMRI reconstruction and motion estimation jointly is formulated as a constraint optimization problem as follows: $$\{\mathbf{f},\mathbf{u}\} = \text{argmin}_{\mathbf{f},\mathbf{u}} \frac{1}{2} || \mathbf{A}(\mathbf{f}) - \mathbf{b} || ^2 +\frac{\lambda}{2}||\mathbf{T}_{\mathbf{f}_0}(\mathbf{u})-\mathbf{f}||^2, \text{s.t.}, ||\mathbf{f}||_1\leq\epsilon,$$ where $$$\mathbf{b}$$$ is the observed k-t data, $$$\mathbf{A}$$$ is the data acquisition operator, $$$\lambda$$$ is the regularization parameter to weight the importance of the OF term. $$$\mathbf{T}_{\mathbf{f}_0}(\mathbf{u})-\mathbf{f} = \mathbf{f}_0 + \nabla_x \mathbf{f}_0 \mathbf{u}_1 + \nabla_y \mathbf{f}_0 \mathbf{u}_2 -\mathbf{f} $$$ is the OF equation, where $$$\mathbf{f}_0$$$ is the reference image, $$$\mathbf{u} = [\mathbf{u}_1,\mathbf{u}_2]^T$$$ is the motion vectors. Note that a reference image is prerequisite in this problem formulation. Fortunately, the idea of the introduction of a reference image in MRI reconstruction has been explored, see e.g., [1]. The constraint promotes the sparsity of the reconstructed images. Since typical heart motions are given by rotation, expansion, contraction,and shear, an affine OF model was implemented. The motion vectors can thus be expressed by $$\begin{cases}\mathbf{u}_1 = \mathbf{u}_{10} + \mathbf{u}_{11}x + \mathbf{u}_{12}y\\\mathbf{u}_2 = \mathbf{u}_{20} + \mathbf{u}_{21}x + \mathbf{u}_{22}y\end{cases}.$$
In order to solve the constraint optimization problem, we firstly reformulate it into a non-constraint version by calculating its augmented Lagrange (AL) function as below $$\text{argmin}_{\mathbf{f},\mathbf{u},\mathbf{g},\mathbf{d}} \frac{1}{2} || \mathbf{A}(\mathbf{f}) - \mathbf{b} || ^2 +\frac{\lambda}{2}||\mathbf{T}_{\mathbf{f}_0}(\mathbf{u})-\mathbf{f}||^2 + \alpha||\mathbf{g}||_1 + \frac{\mu}{2}||\mathbf{f} - \mathbf{g} + \mathbf{d}||^2,$$ where $$$\mathbf{d}$$$ is the AL multiplier and $$$\mu$$$ is the corresponding regularization parameter. An alternating framework is proposed to deal with the formulated problem, which is summarized as below. Specifically, step 1 is addresed using conjugate gradient descent. Step 2 solves the proximal operator of $$$\ell_1$$$-norm term. Step 3 updates the Lagrange multiplier. Step 4 estimates the motion vectors. Note that the motion estimation in step 4 is ill-posed. In this work, a multi-scale technique for affine OF model [2] is implemented to approximate the solution for motion vectors.
$$\begin{array}{l}\text{Proposed Algorithm} \\\text{For}\; k = 0,\ldots\\\left\lfloor\begin{array}{l}1: \mathbf{f}^{k+1} \in \arg\min_\mathbf{f} \frac{1}{2} \|\mathbf{A}(\mathbf{f}) - \mathbf{b}\|^2 \\\;\;\;\; \;\;\;\;\;\;+ \frac{\mu}{2} \|\mathbf{f}-\mathbf{g}^{k}+\mathbf{d}^{k}\|^2 + \frac{\lambda}{2}\|T_{\mathbf{f}_0}(\mathbf{u}^k) - \mathbf{f}\|^2 \\2: \mathbf{g}^{k+1} \in \arg\min_{\mathbf{g}} \alpha \|\mathbf{g}\|_1 +\frac{\mu}{2}\|\mathbf{f}^{k+1}-\mathbf{g}+\mathbf{d}^{k}\|^2 \\3: \mathbf{d}^{k+1} = \mathbf{d}^{k} + \mathbf{f}^{k+1} - \mathbf{g}^{k+1} \\4: \mathbf{u}^{k+1} \in \arg\min_{\mathbf{u}} \frac{\lambda}{2} \|\mathbf{T}_{\mathbf{f}_0}(\mathbf{u}) - \mathbf{f}^{k+1}\|^2\end{array}\right.\end{array}$$
Results
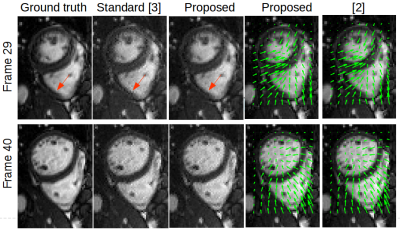
The algorithm was tested on dynamic cardiac cine MRI acquired during free breathing. A 1.5T scanner (MAGNETOM TIM Avanto, Simens Medical Solutions, Erlangen, Germany, resolution = 1.8X1.8X6 mm) was used for data acquisition. The data dimension of the dynamic cardiac cine MRI is $$$70\times50\times50$$$, where the number of frames is 50. The down-sampling ratio is 35% with a golden angle radial trajectory. A standard CS based reconstruction method solved by alternating direction method of multipliers (ADMM) was implemented for comparison [3]. The regularization term in the standard method is $$$\ell_1$$$-norm penalty. According to the results displayed in Fig. 1, the proposed algorithm not only results in lower reconstruction error and more clearly resolves the boundaries (indicates by blue red arrows) than the standard CS method, but also provides competitive performance in the cardiac motion vector estimation compared with [2] (indicates by green arrows).Discussion
The proposed alternating algorithm is capable of jointly reconstructing the dynamic cardiac MRI and estimating the motion vectors. Simulation results demonstrate that the proposed algorithm outperforms the standard method in terms of image reconstruction quality. Future works include more experiments and convergence analysis of the proposed algorithm.Acknowledgements
This work has been supported by NIH grant R01CA188300.References
[1] Ningning Zhao, Daniel O'Connor, Adrian Basarab, Dan Ruan, Ke Sheng, Coupling Reconstruction and Motion Estimation for Dynamic MRI through Optical Flow Constraint, in Proc. SPIE Medical Imaging , Houston, Texas USA, Feb. 2018.
[2] Michael Sühling, Muthuvel Arigovindan and Christian Jansen and Patrick Hunziker and Michael Unser, Myocardial motion analysis from B-mode echocardiograms, IEEE Trans. Image Processing, 2005;14(4):525-536.
[3] Michael Lustig and David L. Donoho and Juan M. Santos and John M. Pauly, Compressed sensing MRI, IEEE Signal Process. Mag.
2008;25(2):72-82.
Figures