Synopsis

Current research in MRI is based on using CS implications to reconstruct high-quality images from a subset of $$$k$$$-space data acquired in an incoherent manner. In this work, we introduce a mathematical framework for improving undersampled MRI data reconstruction, which we call CS+M, where M stands for motion. The significance here, and unlike existing solutions is that by modeling explicitly and simultaneously the inherent complex motion patterns, given by physiological or involuntary motion, in a CS setting, synergies in a complex variational problem are created. These synergies have clinical potentials in terms of improving image quality while reducing motion artifacts.

INTRODUCTION.

METHODS.

Consider an MRI acquisition in which signal measurements of target object $$$u$$$ is collected in spatial-frequency space (i.e. $$$k$$$-space) composed of $$$\mathcal{M}$$$ time samples expressed as $$$s(\mathbf{k},t_{i})=\int_{\mathbf{x}} u(\mathbf{x},t_{i})\exp^{-j\mathbf{k_{i}}^{\intercal}\mathbf{x}} d\mathbf{x} + n(\mathbf{k},t_{i}) \text{ $$$for$$$ } i=1,...,\mathcal{M}$$$ where $$$\mathbf{x}=[x,y]^\intercal$$$ and $$$t$$$ denote the spatial and temporal locations and $$$n$$$ denotes inherent noise during the acquisition. Previous expression can be rewritten in the matrix form $$$y=\mathcal{A}u+n$$$ where $$$y$$$ refers to the $$$\mathbf{k},t-$$$space measurements and $$$\mathcal{A}$$$ is the Fourier operator. Then, reconstruction of the given samples within a standard CS setting can be defined as:

$$[\text{CS}] - arg\min_{u} \frac{1}{2}\parallel\mathcal{A}u-y\parallel_{2}^{2} + \gamma\parallel\mathcal{T}u\parallel_{1}$$

where $$$\mathcal{T}$$$ is the operator promoting sparse representation and $$$\gamma$$$ the regularization parameter. Although CS offers a good reconstruction of the data, it lacks modelling of the inherent motion in MRI settings which may result in a source of artifacts during the reconstruction. One method for modelling physical motion is to use the optical flow constraint which for an image sequence $$$u(x,t)$$$ and velocity field $$$\mathbf{\boldsymbol\upsilon}(x,t)$$$ reads:

$$[\text{M}]- \nabla u \cdot\mathbf{\boldsymbol\upsilon} +\frac{\partial u}{\partial t} =\nabla u \cdot\mathbf{\boldsymbol\upsilon}+u_{t} = 0$$

encoding the intensity invariance assumption. Linking the computation of $$$\mathbf{\boldsymbol\upsilon}$$$ and $$$u$$$ in a single model by variational regularization, our CS+M model is defined as:

$$[\text{CS+M}]-arg\min_{u,\boldsymbol\upsilon} \int_{0}^{T} \bigg( \frac{1}{2}\parallel\mathcal{A}u(\cdot,t)-y(\cdot,t)\parallel_{2}^{2} + \gamma\parallel\mathcal{T}u(\cdot,t)\parallel_{1} + \delta \parallel \nabla\boldsymbol\upsilon(\cdot,t) \parallel_{1} \bigg ) dt \\\text{ subject to } \nabla u \cdot\mathbf{\boldsymbol\upsilon}+u_{t} = 0$$

The benefits of computing motion simultaneously while recovering an image sequence was first proved in$$$^5$$$ for hidden texture datasets and in the medical domain for photoacoustic imaging and X-ray tomography in$$$^{6,7}$$$ respectively.

EXPERIMENTS.

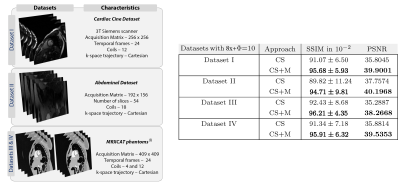
Data description. We used four datasets, described at the left side of Figure 4, for evaluating our approach. Fully sampled data were acquired and then retrospectively undersampled by 8x along ky.

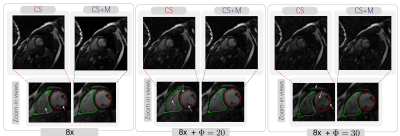
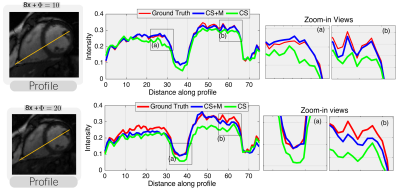
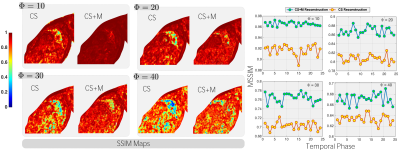
Results. We started evaluating our CS+M against CS approach increasing the undersampling factor for reconstruction by different values ($$$\Phi=10,20,30$$$) and using as reference the fully sampled reconstruction. As shown in Figure 1, our CS+M significantly removed motion artifacts (see white arrows). This, together with the signal intensity profile plots from Figure 2, in which our approach is closer to the reference signal intensity, shows the positive effect of modelling simultaneously the inherent motion during the reconstruction. This is further supported by a quantitative analysis using two gold-standard image quality metrics: the structural similarity (SSIM) index and the Peak signal-to-noise ratio (PSNR). Figure 3 shows the results derived from computing the SSIM index applied on Dataset I, while the table on the right side of Figure 4 shows the complete quantitative analysis for all datasets.

Discussion. Our approach shows higher SSIM, mean SSIM and PSNR than CS, yielding to higher-quality images in comparison with CS while removing artifacts derived from the physiological motion.

CONCLUSION.

Acknowledgements

References

1. Lustig M, Donoho D and Pauly JM. Sparse MRI: The Application of Compressed Sensing for Rapid MR Imaging. Magnetic Resonance in Medicine 2007; 58:1182-1195.\noindent

2. Jung H., Sung K, Nayak K S, Kim E Y and Ye J C. k-t FOCUSS: A general compressed sensing framework for high resolution dynamic MRI. Magnetic Resonance in Medicine 2009; 61: 103–116.

3. Lustig M, Santos J M, Donoho D L and Pauly J M. k-t SPARSE: High frame rate dynamic MRI exploiting spatio-temporal sparsity. In Proceedings of the 13th Annual Meeting of ISMRM, Seattle 2006; Vol. 2420.

4. Otazo R, Candes E and Sodickson DK. Low-rank plus sparse matrix decomposition for accelerated dynamic MRI with separation of background and dynamic components. Magnetic Resonance in Medicine, 2015; 73(3), 1125-1136.

5. Burger M, Dirks H and Schönlieb C-B. A Variational Model for Joint Motion Estimation and Image Reconstruction, arXiv:1607.03255, 2016.

6. Huynh N, Lucka F., Zhang E, Betcke M, Arridge S, Beard P and Cox B. Sub-sampled Fabry-Perot photoacoustic scanner for fast 3D imaging, Proc.SPIE , 2017; Vol.10064.

7. Burger M, Dirks H , Frerking L, Hauptmann A, Helin T and Siltanen S. A Variational Reconstruction Method for Undersampled Dynamic X-ray Tomography based on Physical Motion Models, arXiv:1705.06079, 2017.

8. Wissmann, L., Santelli, C., Segars, W. P. and Kozerke, S. MRXCAT: Realistic numerical phantoms for cardiovascular magnetic resonance. Journal of Cardiovascular Magnetic Resonance, 2014; 16(1), 63.