Synopsis

In this work a method of the reconstruction of magnetic resonance images in the presence of non-rigid motion is presented. A non-rigid deformation model is introduced in the reconstruction problem in order to obtain 1) a motion-free image and 2) a set of non-rigid transformations that describe the motion of the structures being imaged. The method is able to reconstruct the motion information without reconstructing the images in additional motion states avoiding extra computational costs and resulting in a better posed reconstruction problem. Preliminary results for 2D cardiac cine MRI are shown.

Introduction

The presence of motion during MRI examinations is a major source of artifacts and image degradation specially in modalities that require a long acquisition time or when imaging moving organs. Previously proposed approaches to correct motion involve to retrospectively bin the k-space data acquired in different motion states and to reconstruct the corresponding images [1]. Motion can then be estimated with certain image registration method and, once the deformation is known, a motion corrected reconstruction can be performed [2, 3]. The reconstruction of additional motion states involves high computational costs and, in undersampled acquisitions, higher net acceleration factors making their reconstruction more difficult. Moreover, the size of solution space of the reconstruction problem gets multiplied by the number of motion states considered, resulting in a worse posed problem.

In this work, we present a method for the direct reconstruction of a motion-free image plus a set of spatial transformations without the need of additional images. The method departs from the basic assumption that the motion can be described with fewer parameters than the deformed images themselves, resulting in a better posed reconstruction problem. It is a generalization of the method proposed in [4], where only rigid motion is considered.

Preliminary results for 2D, breath-hold cardiac cine MRI are shown, where instead of reconstructing an image for each cardiac phase, a single image is obtained plus a set of deformations describing the motion of the heart.

Theory and Methods

A. Method formulation

The SENSE reconstruction reconstruction problem can be generalized in the presence on non-rigid deformations and formulated as:

$$(\hat{\mathbf{m}}, \hat{\mathbf{\Theta}}) = \arg\min_{\mathbf{m},\mathbf{\Theta}} \|A\mathcal{F} \mathbf{S} \mathbf{T}_ {\Theta} \mathbf{m} - \mathbf{y} \|_2^2$$

where $$$\mathbf{y}$$$ denotes the acquired k-space data, $$$\mathbf{m}$$$ the motion-free image to be reconstructed, $$$\mathbf{S}$$$ the coils sensitivities, $$$\mathbf{T}$$$ the non-rigid transformation matrix governed by the set of parameters $$$\Theta$$$, $$$\mathcal{F}$$$ the discrete Fourier transform and $$$\mathbf{A}$$$ the sampling matrix.

The joint problem can be addressed by iterative solving two subproblems:

1) Image reconstruction:

Considering the deformation $$$\mathbf{T}_{\Theta}$$$ known, we solve

$$\hat{\mathbf{m}} = \arg\min_{\mathbf{m}} \|\mathbf{A}\mathcal{F} \mathbf{S} \mathbf{T}_ {\Theta} \mathbf{m} - \mathbf{y} \|_2^2$$

The problem is equivalent to the one formulated in [2], where the operator $$$\mathbf{G} = \mathbf{A}\mathcal{F} \mathbf{S} \mathbf{T}_ {\Theta}$$$ is defined, and can be solved by means of the conjugate gradient algorithm applied to the system of linear equations given by

$$\mathbf{G}^{H}\mathbf{G} \mathbf{m} = \mathbf{G}^{H} \mathbf{y}$$

2) Motion compensation:

Considering the image $\mathbf{m}$ to be known, the deformation fields are updated by solving

$$\hat{\mathbf{\Theta}} = \arg\min_{\mathbf{\Theta}} \|A\mathcal{F} \mathbf{S} \mathbf{T}_ {\Theta} \mathbf{m} - \mathbf{y} \|_2^2$$.

In this case, the resulting problem is non-linear and can be solved by means of the non-linear conjugate gradient algorithm.

B. Experimental setup.

A regular 2D breath-hold cine MRI was performed in one healthy volunteer with a 32 coil torso antenna in a 3T Philips Achieva TX scanner. Main acquisition parameters include TR/TE/$$$\alpha$$$ = 3.1ms/1.57ms/60$$$^\circ$$$, FOV=320x320mm$$$^2$$$, pixel size=2x2mm$$$^2$$$, 30 cardiac phases. Fully sampled k-space data was retrospectively undersampling simulating a net acceleration factor of 16.

Results and discussion

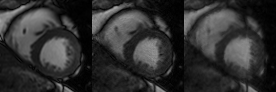
Figure 1 shows the results obtained with the proposed method and with a compressed sensing (CS) reconstruction [5] for an acceleration factor of 16. Fully sampled image is shown as a reference. CS reconstruction presents residual undersampling artifacts and blurred edges in the endocardio. It is worth noticing that, with the proposed method, only one static image is reconstructed. Therefore, the resulting net acceleration factor gets approximately divided by the number of cardiac phases. This aspect explains the capacity of the method to prevent undersampling artifacts.

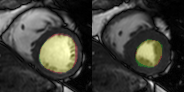
In Figure 2 the left ventricle was manually segmented in the motion-free image and the resulting mask was propagated to the rest of the cardiac cycle. Diastolic and systolic phases are shown with a manual segmentation in the fully sampled images superposed. Excellent agreement between the propagated and manual segmentation can be shown.

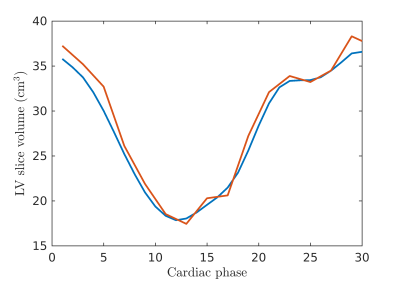
Finally, in figure 3 the slice volumes of the left ventricle through the cardiac cycle obtained from the propagated mask and from manual segmentation are plotted, showing good agreement.

Conclusions

In this work preliminary results of a MRI reconstruction method in the presence of non-rigid motion are presented as a proof of concept. The feasibility of the joint motion and a static image reconstruction approach has been tested and the applicability of the deformations fields to obtain left ventricle volume curves from a single segmentation along the cardiac cycle.

This method can be potentially applied to higher dimensional problems, such as 3D coronary MR angiography in free-breathing and without cardiac gating, where the reconstruction of whole volumes in different cardio-respiratory states to estimate the deformations would imply very high acceleration factors and computational cost.

Acknowledgements

References

[1] Feng et al. (2017), 5D whole-heart sparse MRI. doi:10.1002/mrm.26745

[2] Batchleror et al. (2008), Generalized Reconstruction by Inversion of Coupled Systems (GRICS) applied to free-breathing MRI. MRM, 60:146–157. doi:10.1002/mrm.21623

[3] Cruz et al. (2016), Accelerated motion corrected three-dimensional abdominal MRI using total variation regularized SENSE reconstruction. MRM, 75: 1484–1498. doi:10.1002/mrm.25708

[4] Cordero-Grande et al. (2016), Sensitivity Encoding for Aligned Multishot Magnetic Resonance Reconstruction, IEEE TCI, 2(3):266-280. doi:10.1109/TCI.2016.2557069

[5] Feng et al. (2013), Highly accelerated real-time cardiac cine MRI using k-t SPARSE-SENSE. MRM, 70: 64–74. doi:10.1002/mrm.24440