4081
Fast and Accurate 3D Rigid-Body Motion Information From Spherical Lissajous Navigators at Small K-Space Radii1Institute of Neuroscience and Medicine - 4, Jülich Research Centre, Juelich, Germany, 2RWTH Aachen University, Faculty of Medicine, Department of Neurology, JARA, Aachen, Germany
Synopsis
A new navigator concept is presented which enables the measurement of accurate rigid-body motion information from spherical navigators at extremely small k-space radii. This is achieved by using a 3D Lissajous navigator trajectory and a rotation estimation algorithm known from computer vision. The new method provides motion information with sufficient accuracy and precision for many motion correction techniques and significantly outperforms current spherical navigator methods in terms of acquisition and computation time.
Introduction
Motion is a frequent problem in MRI causing image artefacts which limit clinical and scientific utility. Motion correction techniques have been developed most of which require intra-scan motion information1. Spherical navigators are an efficient way to measure complete rigid-body subject motion using only the available scanner hardware without any external devices. However, current spherical navigator methods, which use helical spiral trajectories2,3, have significant drawbacks limiting their further adoption: Rotation estimation is typically carried out via pattern matching algorithms (PMAs) which are computationally expensive2. Since PMAs require a high amount of magnitude features on the sphere, the navigators need to be acquired at large k-space radii kr≥0.4/cm 2. Unfortunately, however, at large kr, the SNR is low, making the optimal kr a tradeoff between feature richness and SNR3. In addition, current navigator designs exhibit problematic gradient characteristics and require two excitations leading to acquisition times >25ms 2,3.
In this work we present a new spherical navigator concept which overcomes the aforementioned drawbacks. It comprises a spherical Lissajous trajectory which can be acquired in a single shot in less than 10ms with full sphere coverage and gentle gradient requirements throughout4. A spherical harmonics-based rotation estimation known from computer vision5,6 is used which enables accurate estimations from small-kr Lissajous navigators with minimal computational overhead.
Methods
The spherical navigator trajectory used in this work was a 3D Lissajous curve given by
$$k_x=k_r\sin(\omega_{\theta}t)\cos(\omega_{\phi}t)\\k_y=k_r\sin(\omega_{\theta}t)\sin(\omega_{\phi}t)\\k_z=k_r\cos(\omega_{\theta}t)$$
where t is the time, $$$\omega_{\theta}=42\pi/\delta_{nav}$$$, $$$\omega_{\phi}=40\pi/\delta_{nav}$$$ and $$$\delta_{nav}=8ms$$$ is the net navigator duration. Two thousand sampling points were acquired equidistantly in time. The trajectory and the corresponding gradient waveforms are shown in Fig. 1. A non-selective 200μs RF pulse with 15° flip angle was used for excitation. To assess the accuracy of our technique, two series of 121 spherical Lissajous navigators (see Fig. 2) were acquired on a commercial Siemens 3T Trio scanner (Siemens Healthineers, Erlangen, Germany) from a brain-shaped water phantom in a 32-channel head coil. Phantom motion was induced by sinusoidally rotating and translating the FOV by up to 10° about and 10mm along each gradient axis, respectively. In another experiment 450 Lissajous navigators were acquired without moving the FOV, allowing a quantification of the precision, i.e. reproducibility, of the results. Shimming was performed once at the beginning of the measurements using the standard scanner routines.
The Euler angles of the rotations were estimated using an algorithm which was developed for robotic cameras and exploits the rotation theorem of spherical harmonics as described by Makadia et al.5,6. Translations were estimated conventionally by solving an equation system as described by Welch et al.2. The k-space radius of all spherical navigators was kr=0.1/cm and the first navigator of every series was used as the reference. All computations were implemented in Python and performed on a standard laptop with 16GB RAM and a 2.5GHz CPU (Core i7-4710MQ, Intel, USA).
Results
Fig. 3 shows the results for the rotation and translation estimations. The applied FOV motion was accurately extracted from the Lissajous navigators. The maximum deviations from the applied values were below 0.4° and 0.2mm, respectively. Fig. 4 shows the reproducibility of the motion estimations which are very stable and deviate no more than 0.1° and 0.04mm from zero, respectively. The computation times of the complete rigid-body motion estimations from the experiments in Fig. 3 are depicted in Fig. 5. The calculations took on average approx. 65ms and did not exceed 100ms.
Discussion and Conclusions
As shown in this proof of concept, the Lissajous navigator design in combination with the proposed rotation estimation algorithm is, in principle, suited for rigid-body motion measurements from spherical navigators sampled at unprecedentedly small kr. The accuracy and the precision are clearly within the range of what is required for many motion correction techniques. The navigator is acquired more than 50% quicker than in previous techniques2,3 with only a single excitation. Due to the simplicity of the rotation estimation algorithm5,6, the computation times are on the order of tens of milliseconds making this technique significantly faster than previously reported PMA-based approaches2 and applicable to prospective motion corrections.
Since the applied FOV motion was taken as a ground truth although the scanner certainly introduces errors as well, the stated accuracies are worst-case estimates. The investigated motion is still somewhat “artificial” because the phantom itself remained motionless while only the FOV was moved. Our current efforts are towards extending the investigation to “real” motion and switching to a registration-based method as the ground truth. The proposed method has the potential to significantly increase the utility of spherical navigator techniques for motion correction in MRI.
Acknowledgements
No acknowledgement found.References
1Godenschweger F, Kägebein U, Stucht D, Yarach U, Sciarra A, Yakupov R, Lüsebrink F, Schulze P, Speck O. Motion correction in MRI of the brain. Physics in medicine and biology 2016;61:R32
2Welch EB, Manduca A, Grimm RC, Ward HA, Jack Jr CR. Spherical navigator echoes for full 3D rigid body motion measurement in MRI. Magnetic Resonance in Medicine 2002;47:32–41
3Petrie DW, Costa AF, Takahashi A, Yen Y-F, Drangova M. Optimizing spherical navigator echoes for three-dimensional rigid-body motion detection. Magnetic Resonance in Medicine 2005;53:1080–1087
4Ullisch M, Stöcker T, Vahedipour K, Pracht E, Tellmann L, Herzog H, Shah N. Towards Lissajous navigator-based motion correction for MR-PET. Proceedings of the 18th Annual Meeting of ISMRM, Stockholm, Sweden. 2010. p. 3060
5Makadia A, Daniilidis K. Direct 3d-rotation estimation from spherical images via a generalized shift theorem. In: Proceedings of the 2003 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. 2003
6Makadia A, Sorgi L, Daniilidis K. Rotation estimation from spherical images. In: Proceedings of the 17th International Conference on Pattern Recognition, 2004
Figures
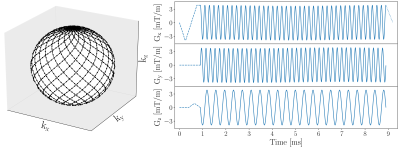
Figure 1: Left: The trajectory of the proposed spherical navigator is a 3D Lissajous curve with full sphere coverage. The black dots indicate the 2000 sampling points equidistantly spaced in time.
Right: The gradient waveforms (solid line) for a Lissajous navigator at kr=0.1/cm. The waveforms are sinusoidal on all axes and never exceed slew rates of 122mT/m/ms. The dashed lines represent start-up gradients necessary to reach the starting position on the k-space sphere and to appropriately bridge the x-gradient. The dotted line is a ramp down gradient which, depending on the application, can also be replaced by a crusher gradient
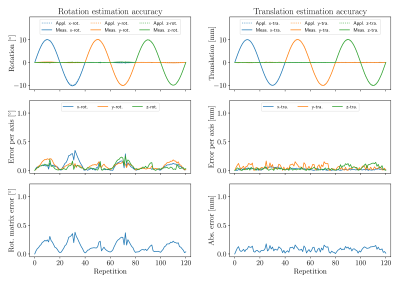
Figure 3: Results of the rotation (left) and translation experiment (right). The top graphs show the measured (solid lines) and the applied motion parameters (dotted lines) for comparison. The centre plots show the errors per axis while the bottom plots show the overall errors.
Measured and applied values are in good accordance such that the dotted lines in the top graphs are barely visible. The rotation and translation estimation accuracy is always better than 0.4° and 0.2mm, respectively. The results demonstrate that the proposed algorithm is capable of accurately estimating rotations about and translations along all coordinate axes.
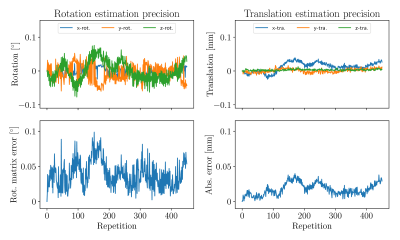
Figure 4: Stability of the Lissajous navigator technique in case of no motion. The plots show the measured rotations (left) and translations (right) with the corresponding errors.
The results are remarkably stable with the rotation and translations estimates deviating no more than 0.1° and 0.04mm from zero, respectively. This good reproducibility is enabled by the high SNR present at small kr.
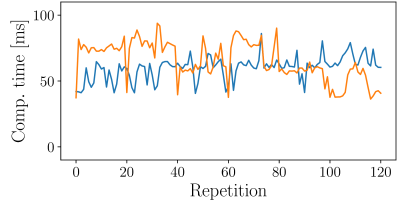
Figure 5: Computation time to obtain the full 3D rigid-body motion estimates of the experiments shown in this work. The orange and blue lines belong to the results shown on the left and right in Fig. 3, respectively.
The computation time on the standard laptop in this work was on average approx. 65 ms and always below 100ms. Although there is still room for improvements in terms of code efficiency, the computation times are already short enough for prospective motion correction applications.