4076
Analysis on pulse shape and temporal resolution effects on RF heating with medical implants1Research and Development, Abbott, Sylmar, CA, United States, 2Research and Development, Abbott, Sunnyvale, CA, United States
Synopsis
MRI RF heating can potentially lead to thermal damages to biological tissues, especially for patients with medical implants, because the RF E-field may induce currents along the implant, leading to concentrated power deposition at implant-tissue interface. Previous methods for computing temperature change through MR scans indicated minimal effect from temporal resolution between 30s and 120s for patients without implants. However, for patients with medical implants, our study suggests that temperature/thermal dose is predicted more accurately with smaller time step sizes (<10s), because immediate response to the heating (increased blood perfusion) needs to be accounted for in a timely fashion.
Introduction
MRI RF heating can potentially lead to thermal damages to biological tissues. In order to assess the accumulative damage through time, the temperature change through MR scans can be estimated with a time course computational model1. The entire scan is divided into discrete time steps, and at each time step, temperature is computed with Penne’s Bioheat equation based on the time-dependent SAR deposition and heat convection and perfusion. The effect of temporal resolution was reported minimal on the temperature calculation from 30s to 120s; this may be sufficient for scans on patients without implants at moderate SAR levels. However, for patients with medical implants (e.g. cardiac leads), the RF E-field may induce currents on the implants, leading to concentrated power deposition at implant-tissue interface and rapid local temperature increment. In this case, the temporal resolution of the computational model becomes critical, because the perfusion rate depending on the instant temperature may not be accurately predicted due to the time lag, resulting in smaller estimated heat dissipation. Therefore, in this study, we investigate the effect of RF pulse shape and temporal resolution on the temperature and thermal dose through time for patients with medical implants.Methods
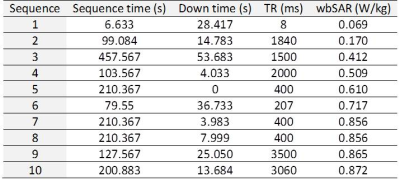
We developed a local temperature/thermal dose calculator for medical implants2. Relevant sequence parameters were extracted from a clinical MRI session of a 67-year-old male consisting of 10 gradient echo sequences with 4ms RF pulse duration for the low-SAR mode (Table 1). Penne’s Bioheat model was used at each time step to calculate the temperature:
$${\rho}C\frac{\partial{T}}{\partial{t}}=K{\triangledown}^2T+{\rho}SAR_{Local}+A-B(T-T_b)$$
For the local hotspot, a (2cm)3 muscle tissue (10g) is examined with thermal properties and coefficients obtained from Wang et al3,4. We simulated the local E-field normalized to a 2 W/kg whole body SAR with a lead implanted inside an adult body model (Duke in Sim4Life).
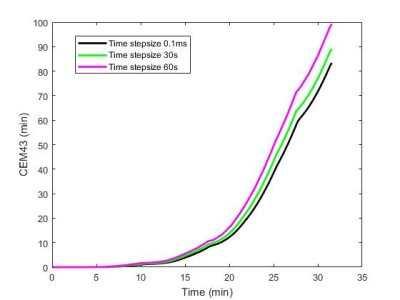
RF pulses of rectangle, sinc and windowed sinc (Figure 1) were examined to determine the effect of pulse shapes on the heating with a temporal resolution of 0.1ms. The E-field was scaled to the pulse amplitude and the sequence parameters such that the total RF energy deposition was maintained. Then we calculated the temperature time course and thermal dose CEM435 using different time step sizes ranging from 0.1ms to 60s. The results from 0.1ms was be used as a gold standard for comparison.
Results
The temperature at the end of the scan is 45.4°C for different pulse shapes (rectangle, sinc and windowed sinc). Despite subtle differences during RF excitation (Figure 2), the temperatures at the end of RF pulse are identical.
For different simulated temporal resolutions, the temperatures and CEM43s at the end of the scan session and maximum temperature deviations from finest temporal resolution are shown in Table 2. The temperature and CEM43 time course of 0.1ms, 30s, and 60s are plotted in Figure 3 and 4, respectively. The maximum temperature difference across all temporal resolutions is 0.29°C. Compared to 0.1ms time step size, the CEM43 is minimally affected by small time steps (<10s). However, the CEM43 values are significantly overestimated when computed with large time steps (30s and 60s).
Discussion
This study confirms that for the same local total power deposition, the pulse shape does not affect temperature change during one TR and the entire scan. The temporal resolution is important to determine the thermal dose for patients with implants. This is because implants locally concentrate the RF energy, resulting in rapid temperature rise. Blood flow and heat convection increases instantaneously to such a change; however, if the step size is chosen too big, the thermal model still uses the temperature from previous step to predict thermal dissipation rate (without updates during the time step), leading to underestimated heat dissipation and overestimated temperature. This effect accumulates over time, resulting in up to 19.1% overestimate in thermal dose when 60s temporal resolution is used.Conclusion
The pulse shape does not affect temperature computations when same amount of heat is deposited locally. For patients with medical implants, the temperature and thermal dose can be accurately predicted with a temporal resolution smaller than 10s.Acknowledgements
No acknowledgement found.References
1. Carluccio G, Bruno M and Collins C. Predicting long-term temperature increase for time-dependent SAR levels with a single short-term temperature response. MRM. 2016 ; 75:2195-2203.
2. Wan Y and Sison S. Framework for computing local temperature and thermal heating through MR session with medical implants. ISMRM. 2018 submitted.
3. Wang Z, Lin J, Vaughan T, et al. Consideration of physiological response in numerical models of temperature during MRI of the human head. JMRI. 2008 ; 28:1303-1308.
4. Wang Z, Lin J, Mao W, et al. SAR and temperature: simulations and comparison to regulatory limits for MRI. JMRI. 2007 ; 26:437-441.
5. Van Rhoon G, Samaras T, Yarmolenko P, et al. CEM43°C thermal dose thresholds: a potential guide for magnetic resonance radiofrequency exposure levels? Eur Radiol. 2013 ; 23(8): 2215–2227. doi:10.1007/s00330-013-2825-y.
Figures