Introduction

Radiofrequency (RF) fields generated by magnetic resonance imaging (MRI) scanners can generate implant-related tissue heating that induces potentially irreversible damage. The results of extensive research devoted to the study of this problem demonstrate that elongated implants could pose a risk to wearers during MRI^1-4. In 2012, the technical specification ISO/TS 10974⁵ was established for testing the safety of implantable parts of active implantable medical devices (AIMD), intended to be used in patients who undergo 1.5T (64 MHz) MRI scans. However, the safety of passive implants, (rods, clips, stents) and small abandoned leads has not yet been systematically assessed. Each device must be tested individually with standard testing methods such as ASTM F2182-11a⁶, even when a small extension is not likely to pose a risk in patients undergoing MRI scans. The mechanism describing exposure enhancement for elongated leads at MRI frequencies is based on energy pick-up by the lead and deposition at critical implant locations, according to a measurable transfer function. It predicts a small dependence of power deposition on the dielectric properties of tissue at the tip of a small abandoned lead, while simulations demonstrate a near-linear dependence on conductivity. In this study, we propose a new mechanistic theory to support a predictive model valid for any small implant that is scalable for frequencies of 3 kHz – 128 MHz. The mechanistic model has been used to derive a standardizable safety assessment approach and to make verifiable predictions about the impact of several parameters.

Methods

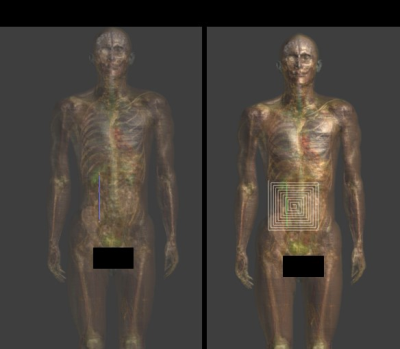
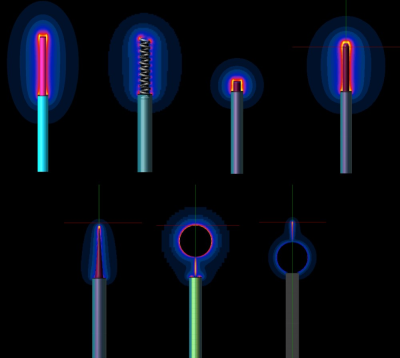
We propose the following mechanistic picture for partially insulated implants significantly shorter than the half-wavelength or resonant length: current is driven through the conducting implant by either the potential difference (electro-quasistatic (QS) regime) or the electromotoric force (magneto-QS). Both are related to the integrated tangential field component along the implant trajectory. Current is forced into the implant ends, requiring that enhanced currents are generated through small cross-sections of tissues with finite conductivity. The overall resistance can be approximated as two series, each inversely dependent on the local tissue conductivity and weakly affected by tip shape. Tip sharpness increases the magnitude of the locally induced fields, but volumetric averaging or thermal diffusion mostly removes that effect. In the absence of insulation, resistance is reduced, but current is distributed over a larger area – hence, the insulated implant constitutes the worst-case. Increasing the frequency results in capacitive coupling through the insulation, reducing its effectiveness and introducing phase considerations, limiting the applicability of the model for implants of length approaching the tissue-specific resonance length. Validation of the mechanism was performed within i) homogeneous setups (different dielectric properties) featuring insulated and bare straight wires of varying length at frequencies from <10 – 128 MHz, ii) with additional local inhomogeneity near the tip, and iii) within complex anatomical models (Figure 1). The parameters investigated include local and spatially averaged electric (E-) fields and current density, peak specific absorption rate (pSAR) averaged on 0.1, 1, and 10 g tissue masses, and temperature increase (dT), as well as SAR to temperature (SAR2T) factors. The dependence on tip shape (Figure 2) and insulation thickness was also simulated.

Results

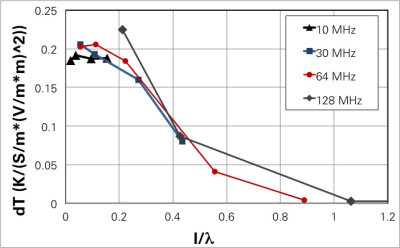
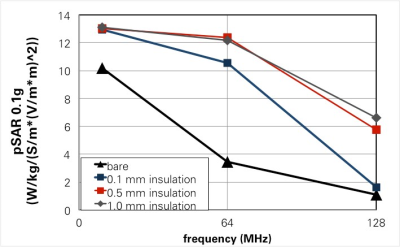
For insulated implants and lengths smaller than the half-wavelength in tissue, the mechanistic model predicts pSAR and SAR2T behavior and parameter dependence (frequency, length, tissue properties, trajectory, shape) with less than 10% variability. For longer insulated leads, a universally scalable behavior-curve across frequencies could be extracted (Figure 3). The expected impact of insulation and its frequency dependence could be qualitatively confirmed (Figure 4). Tip shape not actively considered in the resistance model introduces increased variability requiring safety margins on the order of 20% (pSAR) and 35% (SAR2T).

Discussion and Conclusions

We have developed a quantitative generalized electromagnetic safety model for small implants at MRI frequencies that could be useful for entire passive-implant categories or for corresponding surrogate modelling. For (partially) insulated leads shorter than the half-wavelength in tissue, the deposited power at implant tips depends on the voltage difference between the two tips and is a simple function of the local tissue resistivity at the tips, weakly dependent on tip shape. A universal curve of deposited power and temperature increase as a function of the electrical length is obtained for insulated implants, which extends the applicability of the model to frequencies corresponding to implant lengths comparable to wavelength. The mechanistic model naturally translates to a safety assessment approach (worst-case integrated tangential field trajectory and dielectric properties can be easily identified) that is applicable to MRI safety and at lower frequencies, e.g., for wireless power transfer (WPT) safety.

Acknowledgements

No acknowledgement found.