4037
Ultrafast Temperature Estimation from Undersampled K-Space for MR Guided Microwave Ablation1Department of Biomedical Engineering, Tsinghua University, Beijing, China, 2Center for Biomedical Imaging Research, Department of Biomedical Engineering, Tsinghua University, Beijing, China, 3Department of Orthopedics, First Affiliated Hospital of PLA General Hospital, Beijing, China, 4Key Laboratory of Particle and Radiation Imaging, Ministry of Education, Medical Physics and Engineering Institute, Department of Engineering Physics, Tsinghua University, Beijing, China
Synopsis
Improved fast k-space temperature estimation using Golden Angle (GA) radial can effectively accelerate the computation process and reduce the motion artifacts. However, existing MR temperature imaging methods are time-consuming and the limited performance prevent their clinical applications. This work proposed a ultrafast method to largely accelerate temperature estimation process. Using a continuous fast k-space temperature estimation, together with improved algorithm design, GPU acceleration and more efficient computation, we achieve temperature estimation with 2 seconds temporal resolution.
Purpose
In microwave ablation, it is essential to achieve accurate real-time temperature monitoring for a better control of operation. Considering that PRF-based temperature estimation is very sensitive to motion, the conventional k-space-based hybrid[1,2] approach can improve the accuracy of temperature through combination of hybrid multi-baseline[3] and referenceless[4] method for motion correction. However, existing temperature estimation methods are time consuming due to the large iteration loop and complicated computation. Therefore, this work proposed a method to largely accelerate temperature estimation. Using a continuous fast k-space temperature estimation, together with improved algorithm design, GPU acceleration and more efficient computation, we achieve temperature estimation with 2 seconds temporal resolution.Method
The proposed method estimates temperature changes from undersampled golden-angle (GA) radial data based on hybrid model[1],which can be expressed as:$$y_{i} = \sum_{j = 1}^{N_{s}}e^{i\vec{k_{i}}\vec{x_{j}}}(\sum_{l=1}^{N_{b}}b_{l,j}w_l)e^{i({\{Ac\}}_j+\theta_j)})+\epsilon_i$$
where $$$y_i$$$ is one k-space data sample, $$$N_s$$$ is the number of image voxels, $$$\vec{k_i}$$$ is the k-space location of sample $$$i$$$, $$${\{b_l\}}_{l=1}^{N_b}$$$ are baseline library images acquired before heating with different motion states, $$$w_l$$$ are baseline image weights, $$$A$$$ is a matrix of smooth basis function, $$$c$$$ is a polynomial phase coefficient vector, $$$\theta$$$ is a heating-induced phase shift and $$$epsilon$$$ is complex Gaussian noise [1]. To achieve ultrafast temperature estimation, several acceleration methods are implemented in the algorithm. The detailed steps of our method are shown in Fig. 1. Three main features of this method are as following:
1) K-space data is uploaded to GPU and do parallel computation in each iteration.
2) A low-resolution-image-based parameter estimation method using GA radial is used for acceleration[2,5] .
3) The initial value of temperature in iterations of a particular slice is the temperature estimation of the previous one.
Experimental Designs
The phantom and, in-vivo experiments with heating simulation were implemented to investigate the efficiency and the computation time of the proposed method. The phantom and in-vivo (liver) data with large motion errors due to dynamic acquisition were acquired on a Philips 3T system (Philips Healthcare, Best, the Netherland) respectively.
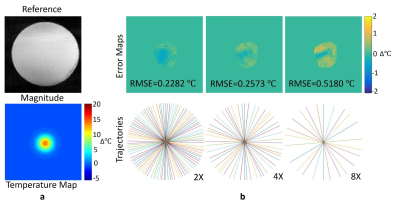
An image of agar phantom without heating was acquired using GA radial sequence for testing the accuracy and the computation time of the proposed algorithm. Then a Gaussian phase was added manually on the images to simulate heating (+25℃). The imaging parameters were: FOV = 160×160 mm2, in-plane resolution = 2×2 mm2, TR/TE = 50/10 ms, flip angle = 15°
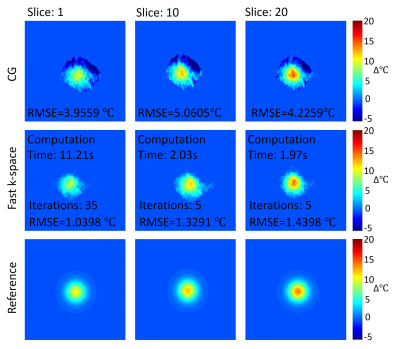
The in-vivo liver experiment with simulated heating was conducted to measure the robustness to motion and the temperature accuracy. The data of 20 slices during the heating process was acquired, using a Cartesian sequence and then converted into GA radial data using NUFFT. The scan parameters were: FOV = 240×307.5 mm2, in-plane resolution = 2×2 mm2, TR/TE = 50/10 ms, flip angle = 15°.
In addition, full-sampled CG temperature reconstructions were also implemented for comparison using the same sampling pattern in each experiment. All our algorithms were implemented on MATLAB 2016b using GPU (GTX 1080 Ti) and CPU respectively. Computation time in each experiment was recorded for comparison.
Results
In phantom heating simulations, the proposed method using GPU showed a relatively lower RMSEs and less computation time: the RMSE of the image at 4x acceleration was 0.2573℃ with less computation time of 3.12s using GPU (6.63s, CPU) (Fig.2)
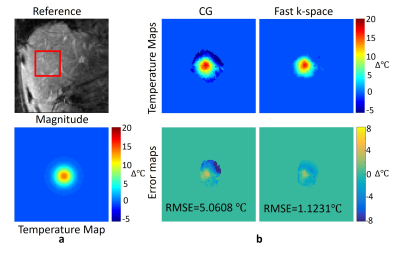
In the liver experiment, the RMSE of the full-sampled CG reconstruction without motion correction was 5.0608℃ while the RMSE of the GA fast k-space reconstruction at 4x acceleration was 1.1231℃ (Fig.3). Based on the GPU acceleration, the computation time was reduced to 5.74s, compared with that using CPU (11.23s). The iteration number and computation time of the continuous temperature estimation was significantly decreased compared with traditional methods (Fig.4), which further accelerated the temperature estimation process.
Discussion and Conclusion
According to the results, both phantom and in-vivo experiments validated the effectiveness of the proposed fast k-space temperature estimation using GPU accelerated GA radial for more accurate temperature estimation and corrected motion-induced errors. In addition, the accelerated acquisition by undersampling and relatively short computation time using GPU makes real-time temperature monitoring for MR-guided microwave ablation possible for clinical applications.
Acknowledgements
This work is supported by Students Research Training (SRT) research funding from Tsinghua University.References
[1] Gaur P, Grissom W A. Accelerated MRI thermometry by direct estimation of temperature from undersampled k-space data.[J]. Magnetic Resonance in Medicine, 2015, 73(5):1914–1925.
[2] Wang F, Dong Z, Chen S, et al. Fast Temperature Estimation from Undersampled k-Space with Fully-Sampled Center for MR Guided Microwave Ablation.[J]. Magnetic Resonance Imaging, 2016, 34(8):1171-1180.
[3] Vigen K K, Daniel B L, Pauly J M, et al. Triggered, navigated, multi-baseline method for proton resonance frequency temperature mapping with respiratory motion.[J]. Magnetic Resonance in Medicine, 2003, 50(5):1003-10.
[4] Grissom W, Pauly K B, Lustig M, et al. Regularized referenceless temperature estimation in PRF-shift MR thermometry[J]. Proceedings, 2009:1235-1238.
[5] Ke Wang et al. p.1749. Proceedings of the ISMRM, 2017
Figures