4032
Combining Compressed Sensing and Parallel Imaging for Accelerating Focused Ultrasound MR Thermometry1Department of Biomedical Engineering, Technion - Israel Institute of Technology, Haifa, Israel
Synopsis
A novel method for accelerated multi-coil Magnetic Resonance guided High Intensity Focused Ultrasound (MRgHIFU) thermometry is presented. This method integrates the two powerful approaches of parallel imaging and Compressed Sensing (CS), and reconstructs temperature rise from sub-sampled k-space data. The proposed reconstruction process utilizes the sparsity of the differences between baseline and post-heating data and operates in a calibrationless manner. The method was validated through a retrospective study of data from a 8-coils in-vivo human prostate treatment and a 2-coils animal experiment.
Background
Magnetic Resonance (MR) thermometry is an efficient tool for monitoring temperature rise in noninvasive thermal treatments such as Magnetic Resonance guided High Intensity Focused Ultrasound (MRgHIFU). It estimates temperature changes by measuring Proton Resonance Frequency (PRF) shifts. However, despite its many benefits, MRgHIFU currently enables temperature monitoring in very few slices during a single sonication. This is due to the relatively long k-space acquisition time. Accelerating acquisition is therefore needed for better coverage of the treated tissue. Several studies considered accelerating PRF thermometry by sub-sampling k-space, utilizing either the parallel MRI approach1,2 or the Compressed Sensing (CS) reconstruction approach3–5. These two approaches showed promising results separately, and have been integrated successfully for non-thermometric MRI applications6–8. Thus, integration of these two approaches may provide a new class of MR thermometry methods.Purpose
In this work, a novel method which combines parallel MRI with CS for MR thermometry is presented. This method utilizes the sparse differences between baseline and post-heating data for recovering temperature changes. The proposed method is suitable for highly sub-sampled multi-coil k-space data, and enables “calibrationless” parallel MR thermometry.Theory
The method assumes the existence of complex-valued baseline images $$$\textbf{x}_0^i \;\; i\in[1,Nc]$$$ where $$$i$$$ is the coil index; these images are obtained from fully sampled k-space data at a pre-heating time $$$t=0$$$. At any later time point $$$t>0$$$, k-space is sub-sampled and the data acquired by coil $$$i$$$ are denoted by $$$\textbf {y}_t^i $$$.The unknown image of this coil at that time is denoted by $$$\textbf{x}_t^i $$$. For simplicity, data from all coils are vector-shaped and concatenated: the vector $$$\bf {x_0} $$$ contains baseline images from all coils, $$$\textbf{y}_t $$$ contains samples from all coils, and $$$\textbf{x}_t $$$ contains the unknown images of all coils.
Since the HIFU alters the image phase at a small region around the focal zone, $$$\textbf{x}_0 $$$ and $$$\textbf{x}_t $$$ are generally very similar. Their complex valued difference $$$\textbf{x}_t-\textbf{x}_0 $$$ is therefore a sparse vector. This work suggests reconstructing $$$\textbf {x}_t $$$ by solving the constrained L1 minimization problem,
$$ \min_{\textbf{x}_t}||\mathbf{\Psi}(\textbf{x}_t-\textbf{x}_0)||_1\; \; \;s.t.\;\tilde{\textbf{F}}_{us}[\textbf{x}_t]={\textbf{y}_t} \;. $$
where $$$\mathbf{\Psi}$$$ is a sparsifying transform, and $$$\tilde{\textbf{F}}_{us}$$$ is an operator that extracts coil-specific data from the concatenated vector, computes the Fourier transform and sub-samples k-space according to the applied undersampling pattern. Notice that this equation promotes multi-coil joint sparsity. We note that a similar approach of complex differences recovery was recently suggested by Cao et al.3 for MR thermometry, however their method was developed for single-coil data and solved a different L1 minimization problem.
The proposed method solves the above equation for every time point $$$t_1,t_2...(t>0)$$$ separately. Then, the phase difference between acquisitions at times $$$t$$$ and $$$t+1$$$ is obtained from the recovered multi-coil data by9,
$$\triangle\phi=atan\left(\sum_{i=1}^{N_c}\textbf{x}^i_{t}\left(\textbf{x}^i_{t+1} \right)^* \right)$$
where $$$*$$$ denotes the complex conjugate operator. Notably, this process utilizes information from all coils, but does not require prior coil sensitivity knowledge, hence it is considered calibrationless.
Methods
Imaging. The proposed method was validated through a retrospective study of data from two scenarios. (1) A porcine brain ablation experiment, performed with a 2 coils array and a 1.5Tesla MR scanner at InSighTech (Tirat HaCarmel, Israel). (2) A human prostate treatment with an 8-coils receiver array, 3Tesla MR scanner (GE Healthcare, Waukesha, WI), and ExAblate 2100 prostate array (InSightec, Tirat HaCarmel, Israel), performed at the Sperling Medical Group center (FA, USA). In all experiments, fully sampled 2D Cartesian k-space data were acquired and retrospectively sub-sampled offline using a random variable-density scheme.
Reconstruction. The L1 minimization problem was solved using the Projection Onto Convex Sets (POCS) approach10, with soft thresholding in the Stationary Wavelet Transform (SWT) domain. The temperatures reconstructed from the sub-sampled data using the proposed method were compared to those obtained from a fully-sampled k-space. All computations were performed in MatLab (The MathWorks, Natick, MA).
Results & Discussion
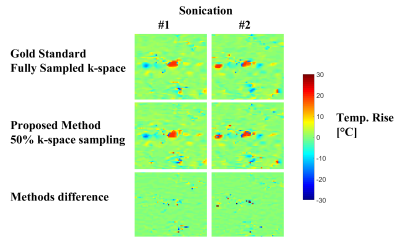
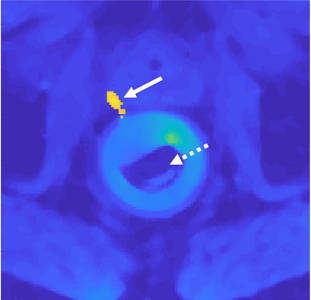
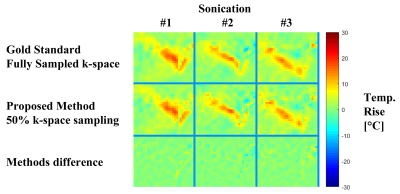
Figure 1 shows results obtained from the in-vivo 2-coils animal experiment. Evidently, the proposed method produced temperature reconstructions very similar to the gold standard ones, both in shape and temperature value. The minor local differences between the two methods (figure 1, third row) are attributed to measurements noise. Figure 2 depicts the anatomical cross section from the 8-coils human prostate treatment, and figure 3 shows the temperature reconstruction results for that treatment. Here also, for all three sonications, our method produced high-quality reconstructions, very similar to the gold standard ones.
These results demonstrate that the proposed approach of combining CS and parallel imaging can effectively shorten acquisition time for MR thermometry.
Acknowledgements
The authors thank Dr. Yoav Levy from InSighTech (Tirat HaCarmel, Israel) and Dr. Dan Sperling from Sperling Medical Group (FA, USA) for providing the in-vivo data, and Dr. Lior Weizman from the Technion (Haifa, Israel) for his valuable comments to this work.References
1. Mei C-S, Panych LP, Yuan J, McDannold NJ, Treat LH, Jing Y, Madore B. Combining two-dimensional spatially selective RF excitation, parallel imaging, and UNFOLD for accelerated MR thermometry imaging. Magnetic Resonance in Medicine. 2011;66(1):112–122.
2. Guo J-Y, Kholmovski EG, Zhang L, Jeong E-K, Parker DL. K-space Inherited Parallel Acquisition (KIPA): application on dynamic magnetic resonance imaging thermometry. Magnetic Resonance Imaging. 2006;24(7):903–915.
3. Cao Z, Oh S, Otazo R, Sica CT, Griswold MA, Collins CM. Complex difference constrained compressed sensing reconstruction for accelerated PRF thermometry with application to MRI-induced RF heating. Magnetic Resonance in Medicine. 2015;73(4):1420–1431.
4. Feng Zhao, Noll DC, Nielsen J-F, Fessler JA. Separate Magnitude and Phase Regularization via Compressed Sensing. IEEE Transactions on Medical Imaging. 2012;31(9):1713–1723.
5. Gaur P, Grissom WA. Accelerated MRI thermometry by direct estimation of temperature from undersampled k-space data. Magnetic Resonance in Medicine. 2015;73(5):1914–1925.
6. Feng L, Grimm R, Block KT, Chandarana H, Kim S, Xu J, Axel L, Sodickson DK, Otazo R. Golden-angle radial sparse parallel MRI: Combination of compressed sensing, parallel imaging, and golden-angle radial sampling for fast and flexible dynamic volumetric MRI. Magnetic Resonance in Medicine. 2014;72(3):707–717.
7. Vasanawala S, Murphy M, Alley M, Lai P, Keutzer K, Pauly J, Lustig M. Practical parallel imaging compressed sensing MRI: Summary of two years of experience in accelerating body MRI of pediatric patients. In: IEEE International Symposium on Biomedical Imaging: From Nano to Macro. IEEE; 2011. p. 1039–1043.
8. Wu B, Millane RP, Watts R, Bones PJ. Prior estimate-based compressed sensing in parallel MRI. Magnetic resonance in medicine. 2011;65(1):83–95.
9. Bernstein MA, Grgic M, Brosnan TJ, Pelc NJ. Reconstructions of phase contrast, phased array multicoil data. Magnetic Resonance in Medicine. 1994;32(3):330–334.
10. Daubechies I, Defrise M, De Mol C. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Communications on Pure and Applied Mathematics. 2004;57(11):1413–1457.
Figures