4031
Fast MRI by Exploiting a Reference Scan (FASTMER) for MR Thermometry1Department of Biomedical Engineering, Technion - Israel Institute of Technology, Haifa, Israel
Synopsis
A Compressed Sensing approach for shortening acquisition time in Magnetic Resonance guided Focused Ultrasound (MRgFUS) thermometry is presented. The approach is based on the recently developed Fast MRI by Exploiting a Reference scan (FASTMER) method. The suggested method embeds into the CS optimization problem a regularization term related to a-priori knowledge about the similarity between pre-heating and post-heating acquired data. The results obtained from an in-vitro Focused Ultrasound (FUS) experiment demonstrate that the proposed method provides efficient and accurate temperature mapping from substantially subsampled k-space data. The method is suitable for data acquired with flexible undersampling schemes.
Background
Magnetic Resonance guided Focused Ultrasound (MRgFUS) treatments rely on rapid temperature mapping provided by MR thermometry. MRgFUS has been proven successful for a range of clinical applications1,2. Nonetheless, real-time applications of MRgFUS are currently limited to several slices within a single sonication. Evidently, acquisition time can be shortened by reducing the amount of data sampled in k-space. Methods proposed for temperature reconstruction from under-sampled k-space have utilized the benefits of Compressed Sensing (CS) reconstruction3,4 or temporal regularization5–8. The CS approach assumes image sparsity in a known transform domain, and the temporal regularization approach assumes a slow temporal change of image data during treatment. A more recent approach utilized both of these concepts and proposed temperature reconstruction by recovery of complex differences from baseline images9.
This work proposes a temperature reconstruction scheme which merges the two above approaches in different manner. The proposed scheme utilizes the fact that the difference between baseline and post-heating data is sparse. This a-priori knowledge is embedded into the CS optimization problem by an additional regularization term. The proposed scheme is based on the novel framework of Fast MRI by Exploiting a Reference scan (FASTMER)10,11 for reconstruction from sub-sampled k-space data.
Theory
The CS reconstruction framework exploits data sparsity under a known transform $$$\bf{\Psi}$$$, which is typically the wavelet transform. CS algorithms conventionally solve the unconstrained optimization problem,
$$\min_{\textbf{x}}||\textbf{F}_u\textbf{x}-\textbf{y}||_2^2+\lambda_1||\mathbf{\Psi}\textbf{x}||_1 \;\;\quad(1)$$
where $$$\bf{x}$$$ is the vector-shaped complex image to be reconstructed, $$$\bf{y}$$$ are the concatenated k-space measurements, $$$\lambda_1$$$ is a regularization parameter, and $$$\textbf{F}_u$$$ is a sub-sampled Fourier transform operator. While the above equation has been implemented successfully for CS-MRI5, it does not utilize any baseline information, which naturally exists in MR thermometry scans.
To exploit a fully-sampled baseline image $$$\textbf{x}_0$$$ acquired before the therapeutic energy deposition, we utilize the FASTMER framework11,10. Since the thermal ablation treatments commonly modify only the phase in a relatively small area, the complex-valued images $$$\textbf{x}_0$$$ and $$$\textbf{x}$$$ are generally highly similar. The FASTMER method incorporates this prior knowledge into eq. (1) by adding a regularization term that promotes similarity between $$$\textbf{x}_0$$$ and $$$\textbf{x}$$$ ,
$$\min_{\textbf{x}}||\textbf{F}_u\textbf{x}-\textbf{y}||_2^2+\lambda_1||\textbf{W}_1\mathbf{\Psi}\textbf{x}||_1+\lambda_2|| \textbf{W}_2\left(\textbf{x}-\textbf{x}_0\right)||_1 \;\;\quad(2)$$
where $$$\textbf{W}_1$$$ and $$$\textbf{W}_2$$$ are diagonal weighting matrices controlling the sparsity and similarity requirements respectively, and $$$\lambda_1$$$ and $$$\lambda_2$$$ are regularization parameters. The weights $$$\textbf{W}_2$$$ enable reduction of the similarity requirement at pre-defined areas, such as the FUS ablation zone.
Methods
In vitro Phantom Experiment
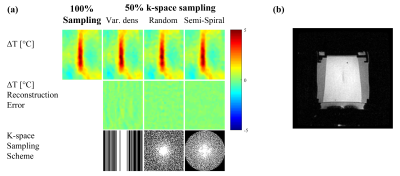
The proposed method was evaluated by retrospective undersampling of full k-space data acquired during a FUS heating experiment of an in vitro phantom, performed with a 3T GE scanner at Stanford University School of Medicine. Three k-space undersampling schemes were implemented: 1D variable density undersampling, 2D variable density random undersampling, and semi-spiral undersampling (figure 1).
CS Reconstruction
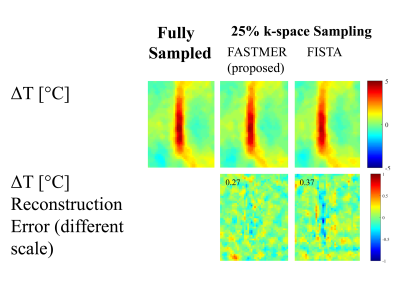
In the proposed FASTMER method, the non-convex L1 regularization problem (eq. (2)) was solved using an extended SFISTA algorithm11, with Daubechies wavelets and $$$\lambda_1=0.01,\; \lambda_2=0.02$$$. Additionally, $$$\textbf{W}_2$$$ was nulled in the pre-defined FUS ablation area to loosen the similarity requirement. The FASMTER temperature reconstruction was compared to a gold standard temperature map obtained from the fully-sampled data and to results obtained by the popular FISTA algorithm solving eq. (1).
Results & Discussion
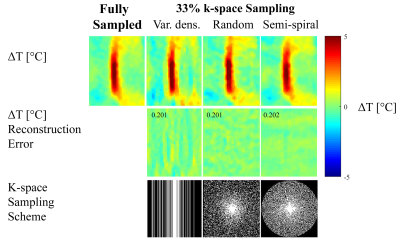
Figure 1 shows temperature reconstructions obtained from a 2-fold sub-sampled k-space using the proposed method, for three different undersampling schemes. The gold standard reconstruction obtained from the fully sampled data is also shown for comparison (figure 1, top row). In all cases, the reconstructed temperature accuracy was high both structurally and quantitatively. This high reconstruction accuracy is reflected by the low reconstruction error maps (figure 1, second row), which exhibit a maximal reconstruction error of about 1°C. Similar high-quality results were obtained for a higher undersampling factor of 3, for all three reconstruction schemes, as shown in figure 2.
Figure 3 shows a comparison between the proposed FASTMER reconstruction, that solves eq. (2), and a more conventional FISTA reconstruction solving eq. (1) (figure 3, first row). Both methods were implemented on k-space data undersampled with a 4-fold acceleration and semi-spiral sampling scheme. FASTMER obtained a high quality temperature reconstruction with an NRMSE of 0.27, while FISTA produced a less accurate reconstruction with an NRMSE of 0.37 (figure 3, second row).
Conclusion
This work suggests a new compressed sensing based approach for accurate MR thermometry. It reconstructs highly accurate temperature maps from sub-sampled k-space data by exploiting similarity to fully-sampled baseline data. This method also enables flexible k-space undersampling schemes. It accelerates MR thermometry, thus allowing the acquisition of more slices and coverage of a larger volume per given scan time during MRgFUS.Acknowledgements
The authors thank Prof. Kim Butts Pauly and Dr. Pooja Gaur from Stanford University for providing the in-vitro data and for their valuable comments.References
1. Ghanouni P, Pauly KB, Elias WJ, Henderson J, Sheehan J, Monteith S, Wintermark M. Transcranial MRI-Guided Focused Ultrasound: A Review of the Technologic and Neurologic Applications. American Journal of Roentgenology. 2015;205(1):150–159.
2. Pauly KB, Diederich CJ, Rieke V, Bouley D, Chen J, Nau WH, Ross AB, Kinsey AM, Sommer G. Magnetic Resonance-Guided High-Intensity Ultrasound Ablation of the Prostate. Topics in Magnetic Resonance Imaging. 2006;17(3):195–207.
3. Feng Zhao, Noll DC, Nielsen J-F, Fessler JA. Separate Magnitude and Phase Regularization via Compressed Sensing. IEEE Transactions on Medical Imaging. 2012;31(9):1713–1723.
4. Leonard P, Chopra R, Nachman A. Compressed Sensing for Accelerated MR Thermometry in MRI-Controlled Transurethral Ultrasound Therapy. In: Proc. Intl. Soc. Mag. Reson. Med. Vol. 20. 2012.
5. Gaur P, Grissom WA. Accelerated MRI thermometry by direct estimation of temperature from undersampled k-space data. Magnetic Resonance in Medicine. 2015;73(5):1914–1925.
6. Todd N, Adluru G, Payne A, DiBella EVR, Parker D. Temporally constrained reconstruction applied to MRI temperature data. Magnetic Resonance in Medicine. 2009;62(2):406–419.
7. Todd N, Prakash J, Odéen H, de Bever J, Payne A, Yalavarthy P, Parker DL. Toward real-time availability of 3D temperature maps created with temporally constrained reconstruction. Magnetic Resonance in Medicine. 2014;71(4):1394–1404.
8. Roujol S, Ries M, Quesson B, Moonen C, Denis de Senneville B. Real-time MR-thermometry and dosimetry for interventional guidance on abdominal organs. Magnetic Resonance in Medicine. 2010;63(4):1080–1087.
9. Cao Z, Oh S, Otazo R, Sica CT, Griswold MA, Collins CM. Complex difference constrained compressed sensing reconstruction for accelerated PRF thermometry with application to MRI-induced RF heating. Magnetic Resonance in Medicine. 2015;73(4):1420–1431.
10. Weizman L, Eldar YC, Ben Bashat D. Compressed sensing for longitudinal MRI: An adaptive-weighted approach. Medical Physics. 2015;42(9):5195–5208.
11. Weizman L, Eldar YC, Ben Bashat D. Reference-based MRI. Medical Physics. 2016 [accessed 2017 Feb 20];43(10):5357–5369. http://doi.wiley.com/10.1118/1.4962032. doi:10.1118/1.4962032
12. Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magnetic Resonance in Medicine. 2007;58(6):1182–1195.
Figures