4027

Probehead design for multi-photon NMR induced homonuclear continuous RF decoupling
Christoph Michael Schildknecht1, David Otto Brunner1, and Klaas Paul Pruessmann1

1Institute for Biomedical Engineering, ETH Zurich and University of Zurich, Zurich, Switzerland

Synopsis

Spectra of strongly coupled nuclear systems are frequently obtained by fast magic angle spinning. In biological samples, this is often not feasible, leaving homonuclear RF decoupling as the only alternative. This approach requires fast nutation while receiving a spectrum from the same type of nuclei. This can be achieved by multi-photon excitation, albeit at the expense of high power densities. In this work, we present a construction approach for such probe heads maximizing the excitation efficiency and demonstrating nutations above 20kHz over extended periods of time.

Introduction

Homonuclear coupling is one of the major obstacles in NMR assessment of larger biologically relevant molecules because it can broaden the lines of strongly coupled spin systems beyond recognition. Nowadays, this broadening is reduced typically by magic angle spinning (MAS) if the sample can be rotated with over 100’000 rpms. Obviously, many biological samples cannot withstand these centrifugal forces or cannot be fitted into the rotator.

Alternatively, homonuclear RF decoupling can be applied in a Lee-Goldburg based irradiation scheme1. Here however, fast spin nutations have to be induced ideally without interrupting the acquisition of the NMR signal. This can be achieved by multi-photon excitation.

A subgroup of multi-photon excitation is the two-photon excitation which has two excitation fields. Compared to traditional MRI and NMR, two-photon excitation has the ability to simultaneously excite and acquire nuclear spins with minimal crosstalk. Any RF fields, with both perpendicular and parallel field components relative to the main magnetic field, which sum up or differ by the NMR frequency excite the nuclear spins. Therefore transmission and reception are frequency-multiplexed and the NMR signal can be isolated by sufficiently rejecting the transmission frequencies in the receive path1,2,3.

Prior work demonstrated the validity of this concept and achieved a maximum nutation frequency of 20 kHz using 500 W on a coil with 360 um diameter1. However, to decouple strongly coupled coherences, higher nutation frequencies are required. The nutation speed is limited by the excitation efficiency of the two-photon excitation and the power handling capability of the probehead.

In this work we address these limitations by a novel probehead design and construction of a proton-free prototype. While a tilted coil was employed in Ref. 1 the novel setup is equipped with three orthogonal coils and operates at a significantly lower modulation frequency enhancing the efficiency of the approach. The power handling was increased by providing a liquid cooling system in the probehead.

Theory and Methods

The two-photon excitation process can be described by the average Hamiltonian theory4. Assumed $$$ w_{mod} <<w_{transmit}$$$, the nutation frequency can be approximated by $$ w_{nut} = \frac{\gamma^2B_1\cos(\theta_1)B_2\sin(\theta_2)}{4w_{rf1}} $$. Enabling a small $$$w_{mod}$$$ and an orthogonal coil arrangement ($$$\theta_1=0 $$$ $$$\theta_2=\pi/2 $$$) is hence key to provide a high power efficiency4.

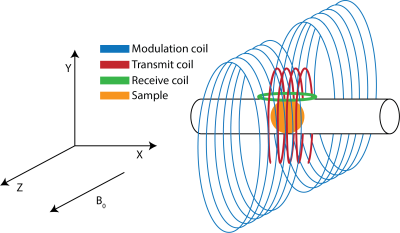
The probehead, shown in Fig. 1, is equipped with dedicated coils for reception, transmission if the high-frequency field and the modulation field. This allows to individually design each coil for optimal efficiency and the required uniformity. For integration, the designs were co-optimized by a genetic algorithm employing quasi-stationary field calculations for evaluation of the fitness.

The coils are submerged in FC-72 liquid in order to improve the power handling capability and the $$$B_0$$$ uniformity in the sample.

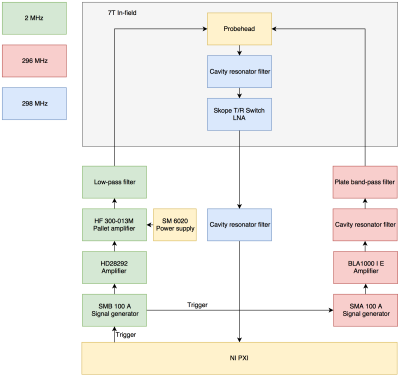
A schematic of the custom assembled experimental setup is shown in Fig. 2.

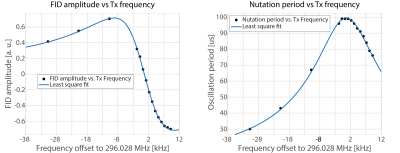
To measure the achieved nutation frequency, two methods have been employed. First, trajectories of the spin evolution during 10ms irradiation with constant power and different RF frequency offset (-30-10 kHz) were recorded. The frequency of the initial amplitude oscillations and signal strength of the FID after settling were then fitted to a theoretical model (Fig. 4). Alternatively, the signal magnitude of the FID as a function of the length of effectively on-resonant excitation block pulses was measured and fitted.

Results

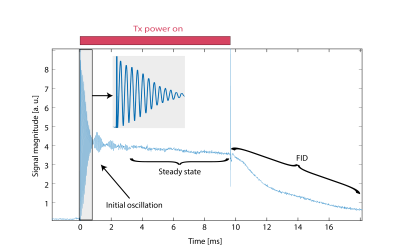
During a period of constant irradiation, an example spin behavior can be seen in Fig. 3. Initially strong oscillations from off-axis nutation of the spins can be seen which settles in a spin-lock. Turning off RF irradiation is followed by an FID.

With 300 watt of modulation power and 4 watt of RF power, a nutation frequency of 20.2 kHz could be observed.

Discussion & Conclusion

A significant improvement in excitation efficiency could be demonstrated by the novel setup allowing for a lower modulation frequency and using distinct orthogonal coils for transmission and reception. As shown in Fig. 5, the excitation efficiency per magnitude of excitation field strength was improved by a factor of 21 compared to Ref. 4 and by a factor of 75 relative to Ref. 1. Further advances are expected by reducing the number of turns of the high-frequency transmit coil, which will move it further away from self-resonance. By enhancing the RF power from currently 4 watt to the order of 100 watt, nutation frequencies well above 100 kHz should be achievable with net power below 500 watt. Such nutation frequencies should allow to highly resolve spectra of large molecules, some protein backbones, or NMR spectra from magnetoacoustic5 or piezoelectric6 materials.

Acknowledgements

No acknowledgement found.

References

1. C. A. Michal, S. P. Hastings, and L. H. Lee, “Two-photon lee-goldburg nuclear magnetic resonance: Simultaneous homonuclear decoupling and signal acquisition” The Journal of Chemical Physics, vol. 128, no. 5, p. 052 301, 2008

2. P. T. Eles and C. A. Michal, “Two-photon excitation in nuclear magnetic and quadrupole resonance” Progress in Nuclear Magnetic Resonance Spectroscopy, vol. 56, no. 3, pp. 232-246, 2010.

3. D. O. Brunner, et al Sideband Excitation for Concurrent RF Transmission and Reception, Proc. Intl. Soc. Mag. Reson. Med. 19 (2011)

4. P. T. Eles and C. A. Michal, “Two-photon two-color nuclear magnetic resonance” The Journal of Chemical Physics, vol. 121, no. 20, pp. 10 167-10 173, Nov. 2004.

5. E. Fukushima, S.B.W. Roeder, Spurious ringing in pulse NMR, J. Magn. Reson. 33 (1979) 199–203

6. D.G. Hughes, L. Pandey, Spurious signals caused by the piezoelectric ringing of NaNO2 in pulse NMR, J. Magn. Reson. 56 (1984) 428–442.

Figures

Figure 1: The coils for signal reception, high frequency RF transmission and generation of the modulation field are orthogonally mounted in layers around the sample to the outside. The modulation coil produces a field colinear with B0, while the receive and the transmit coil are oriented orthogonal to each other and to be sensitive for transverse magnetic field components. A channel isolation from the transmit coil to the receive coil of -16 db was achieved. The entire probehead was constructed from proton free materials such as borosilicate class and PTFE in order to avoid stray NMR signals in the acquisition.

Figure 2: Block diagram of the entire experimental setup. The receive path (blue) is protected against the RF transmission signal by highly selective and low loss stopband filters made from cavity resonators. Noise from the transmit chains for modulation (green) and RF (red) is filtered on the NMR frequency before entering the Faraday cage.

Figure 3: Time evolution of the signal magnitude of a 400nl water sample under concurrent irradiation of a 10ms block pulse. The 2 MHz modulation field was driven with 300 watt and 1 watt were sent into the RF transmitter. The RF pulse was delayed by 300us to accommodate for the ring-up of the modulation coil. Third order intermodulation products were subtracted from the data. The spikes at the beginning and ending of the pulse are generated by the steep and broadband flanks of the employed block modulation.

Figure 4: During an interval of constant irradiation (Fig. 3), initial oscillaction frequency and the FID amplitude change depending on the frequency offset ($$$ f = \sqrt{ \omega_1^2+(\omega_{BS}-\Delta\omega)^2} , S=S_0\frac{\omega_1(\omega_{BS}- \Delta\omega)}{(\omega_1^2+(\omega_{BS}^2-\Delta\omega)^2)} $$$ with nutation frequecy $$$\omega _1$$$, Bloch-Siegert shift $$$\omega _{BS}$$$, irradiation offset $$$\Delta\omega $$$ and FID constant $$$S_0$$$ ). Fitting these values to the theoretical formulas allows measurement of the nutation frequency1. The results in this figure were optained by irradiating 300 watt modulation power and 1 watt RF power.

Figure 5: Quantitative comparison to related work. With field efficiency is defined as nutation frequency per magnitude of field strength. The power efficiency is the nutation rate per product of the square root of both excitation fields. It does not apply to the half resonance excitation efficiency because it scales with a different order.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
4027