Synopsis

The current work presents a novel approach on signal enhancement in magnetic resonance spectroscopy through explicit field perturbatiobn. We have discovered that under certain conditions of artificial perturbation of the existing field, the output signal can be enhanced. The signal enhancement not only happens by increasing the magnitude of the external signal at the precession frequency but also by changing the frequency of the external field. The results have broad application not only in the field of magnetic resonance spectroscopy but also in magnetic resonance imaging.

Introduction

Methods

External field perturbation results in addition of noise which degrades the signal. However, in a phenomenon like stochastic resonance (SR), a weak signal is amplified under the addition of noise in a bistable systems separated by an energy threshold [1]. The broadband noise reduces the energy threshold between the two stable states inducing a change of state and signal enhancement.

A magnetized sample of nuclei under static magnetic field has two stable states separated by an energy threshold [2]. SR has been observed in electron paramagnetic resonance based systems [3] and SR based transform in Fourier domain by adding an optimized level of Gaussian fluctuation that maximizes signal-to-noise ratio has been used for the enhancement of MR images of brain lesions [4].

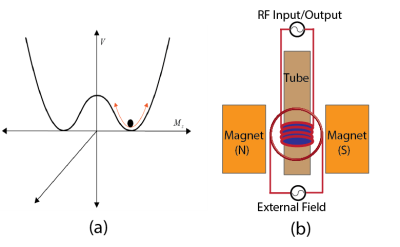
A bistable system can be defined by a symmetric quartic potential (Fig. 1a), V(q)=-aq²/2+bq²/2, where q indicates the spatial coordinate, a and b are constants which can be assumed to be unity. The signal generated under transition of states can be written as, v(t)=-V'(q)+u₀cos(ωt) +ξ(t). Here, V'(q) is the energy gradient, u₀cos(ωt) is the excitation signal with a frequency ω at time t and ξ(t) is the noise. The rate of transition between the two states is defined by Kramers rate, r_K=0.22(e^{- ΔV/D}), where ΔV is the height of the barrier and D is energy of noise level. It indicates that as the noise level increases, the rate of transition increases.

Experiments were done with the objective of generating external field perturbation in order to explore signal enhancement similar to stochastic resonance.

The measurements were done on a sample of copper sulphate solution with Hydrogen ions at the precession frequency of 21.65 MHz inside a portable permanent magnet (Metrolab Instruments), Bo = 0.5 T, with a console (Kea Magritek). A detection coil of 2 mm diameter with a microcapillary tube of outer diameter 1500 μm and inner diameter 950 μm for a sample volume of 300 nl was mounted on a single PCB. Each experimental data set was collected by one pulse pulse program, 90 degree pulse width of 6 μs and power of 12.5 mW with 4 set of scans comprising an acquisition time of 2000 ms.

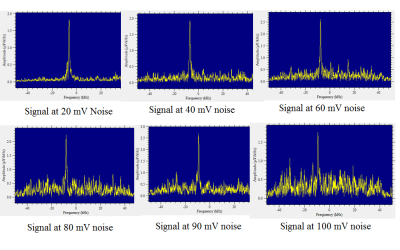
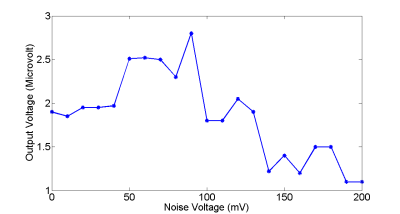
Initially, the MR signal was recorded and the output voltage was measured to be 1.8 µV. A 5 turn 2.5 cm radius RF coil, place at a distance of 2 cm from the sample, aligned perpendicular to the B₀ and B₁ field was .excited by a broadband noise signal from 10 mV to 1 V (Fig. 2) to generate field perturbation. As the noise power was raised, there was an enhancement of signal progressively until 80 mV after which noise started getting enhanced and the signal level dropped (Fig. 3). There was some enhancement of noise signal, however, the total enhancement of signal level was higher than that of noise.

The magnetic moment of Hydrogen nuclei is 1.4×10^-26 J/T. The approximate value of energy of transition in a sample of volume 100 nL is 0.841 µJ. The effective value of perturbation field was in the range of 10 nT to 100 nT as the coil noise voltage was varied from 20 mV to 100 mV and was lower by a factor of 4 in comparison to the B₁ field.

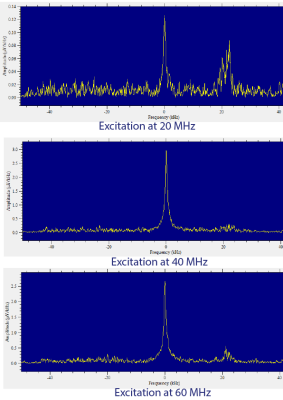
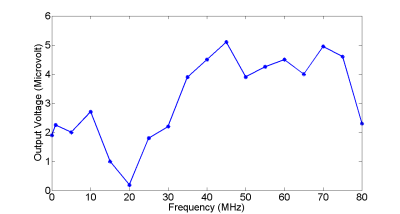
Subsequently, field perturbation was achieved by exciting the external coil at frequencies from 20 MHz to 80 MHz while maintaining a steady value of 100 nT excitation . At 20 MHz excitation and a field of 100 nT, the external field attenuates the MR signal significantly and an output voltage of 0.14 µV was obtained (Fig. 4). The output signal increases rising to a maximum value at 40 MHz and then decreases. (Fig. 5).

Results

Discussion

Conclusion

Acknowledgements

References