4016

Removal of Water Sidebands from 1H-MRSI Data Acquired without Water Suppression
Yudu Li1,2, Fan Lam2, Rong Guo1,2, Bryan Clifford1,2, Xi Peng2,3, and Zhi-Pei Liang1,2

1Department of Electrical and Computer Engineering, University of Illinois at Urbana-Champaign, Urbana, IL, United States, 2Beckman Institute for Advanced Science and Technology, University of Illinois at Urbana-Champaign, Urbana, IL, United States, 3Paul C. Lauterbur Research Center for Biomedical Imaging, Institutes of Advanced Technology, Shenzhen, China

Synopsis

The water sideband artifact is a major obstacle to proton MR spectroscopic imaging (1H-MRSI) without water suppression (WS). This work presents a novel method to remove the sideband artifacts from non-WS MRSI data, characterized by the use of a reference-based parametric model to represent the artifacts. Our method obtains the reference signal from two auxiliary scans and subsequently estimates the sideband signals from a particular MRSI data. The proposed method has been validated using both phantom and in vivo experimental data, demonstrating that it can effectively remove the sideband artifacts without introducing spectral distortion. This method is expected to be useful for many non-WS MRSI studies.

Introduction

Standard proton MR spectroscopic imaging (1H-MRSI) methods rely on water suppression (WS) pulses to significantly reduce the dominant water signals. However, the introduction of WS pulses may distort the metabolite signals and increase the total acquisition time. These disadvantages motivate the development of MRSI without WS, which provides additional advantages including the use of the unsuppressed water signals for correction of the inter-voxel B0 inhomogeneity and lineshape distortions. A major practical issue associated with non-WS MRSI is the existence of sideband artifacts in the MR spectra. These artifacts largely overlap and can be on the same order or even larger than the metabolite signals, which makes spectral quantification and other data analysis challenging1. To address this problem, we proposed a signal processing based sideband removal method characterized by the use of a reference-based parametric model to represent the sideband artifacts. The proposed method has been evaluated using both phantom and in vivo data, demonstrating effective removal of water sidebands.

Method

Signal model for sideband artifacts

The sideband artifacts at spatial location $$$\boldsymbol{x}$$$ can be modeled as the sum of the frequency modulations of the associated unsuppressed water signal1. More specifically, we express the sideband signal with $$$N$$$ prominent components as:

$$\hspace{13.5em}S_{side}(\boldsymbol{x},t)=\sum_{n=1}^{N}\tilde{S}_{n}(\boldsymbol{x},t){e^{-\beta_{n}(\boldsymbol{x})t}}S_{w}(\boldsymbol{x},t),\hspace{13.5em}(1)$$

where $$$\{\tilde{S}_n\}$$$ are the carrier functions, $$$\{\beta_n\}$$$ the damping factors and $$$S_w$$$ is the unsuppressed water signal. One possible form of $$$\tilde{S}_n$$$ is an FIR filter with unknown frequency locations. However, this representation would require the estimation of the sideband signals directly from the measured MRSI data which may contain significant spectral distortions because of the overlap between metabolites and sideband signals. To avoid this, we propose a reference-based signal model for sideband signals which represents the carrier functions as the convolution of a reference signal $$$S_{ref,n}(t)$$$ and FIR filters with fixed frequencies:

$$\hspace{13.5em}\tilde{S}_n(\boldsymbol{x},t)=S_{ref,n}(t)\sum_{p=-P}^{P}\tilde{c}_{p,n}(\boldsymbol{x}){e^{i2{\pi}pΔft}},\hspace{13.5em}(2)$$

where $$$Δf$$$ is the frequency resolution and $$$\{\tilde{c}_{p,n}\}$$$ are spatially dependent coefficients. $$$S_{ref,n}(t)$$$ can be estimated from auxiliary scans and is chosen to have to the following form:

$$\hspace{12.65em}S_{ref,n}(t)=({e^{i2{\pi}f_{n}t}}-{e^{-i2{\pi}f_{n}t}})\sum_{l=-L}^{L}c_{l,n}{e^{i2{\pi}lΔft}}.\hspace{12.65em}(3)$$

This model is motivated by the fact that the prominent sideband peaks are symmetrically located on both sides of the main water peak with opposite phases.

Algorithm

The proposed model enables removal of the sideband artifacts in two steps: 1) estimation of $$$S_{ref,n}(t)$$$ from auxiliary scans, and 2) estimation of $$$S_{side}(\boldsymbol{x},t)$$$ for a particular MRSI dataset.

In this work, we estimate the reference signal from two navigator signals $$$S_{nav,1}(t)$$$ and $$$S_{nav,2}(t)$$$ acquired at the k-space origin with and without WS respectively. After removal of the residual water signals (e.g., using HSVD2), their difference signal $$$S_{diff}(t)$$$ should contain negligible metabolites but keep the sideband artifacts. We then solve the following optimization problem:

$$\hspace{7.75em}\min_{f_n,c_{l,n},\beta_n}||S_{diff}(t)-\sum_{n=1}^N\{({e^{i2{\pi}f_nt}}-{e^{-i2{\pi}f_nt}})\sum_{l=-L}^{L}c_{l,n}{e^{i2{\pi}lΔft}}\}{e^{-\beta_n(\boldsymbol{x})t}}S_w(t)||_2^2.\hspace{7.75em}(4)$$

The optimal solution to the above problem will be used to synthesize the reference signal based on Eq. (3).

Even with the reference signal $$$S_{ref,n}(t)$$$, estimation of the sideband artifacts from the original MRSI data is still possible to include some metabolites due to determination of the FIR filter in Eq. (2) (even though $$$P$$$ is usually small). To overcome this, inspired by QUEST3, we fit the metabolite signals after truncating an appropriate number of initial points and then subtract the back-extrapolation of these estimated metabolites from the original data to obtain the metabolite reduced signal $$$\hat{S}(\boldsymbol{x},t)$$$. This strategy is appropriate since the sideband signals usually have much higher decay rates than common metabolites1. The final estimates of the unknown parameters in Eq. (1) and Eq. (2) are obtained by solving the following optimization problem:

$$\hspace{9em}\min_{\tilde{c}_{p,n},\beta_{n}}||\hat{S}(\boldsymbol{x},t)-\sum_{n=1}^{N}S_{ref,n}(t)\sum_{p=-P}^{P}\tilde{c}_{p,n}(\boldsymbol{x}){e^{i2{\pi}pΔft}}{e^{-\beta_n(\boldsymbol{x})t}}S_w(\boldsymbol{x},t)||_2^2.\hspace{9em}(5)$$

Results

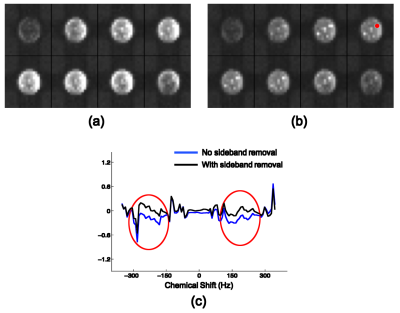
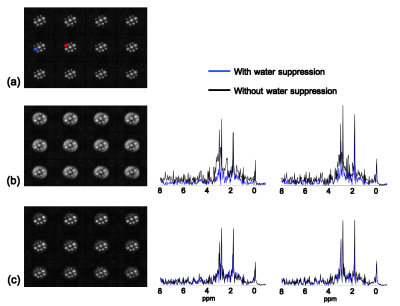
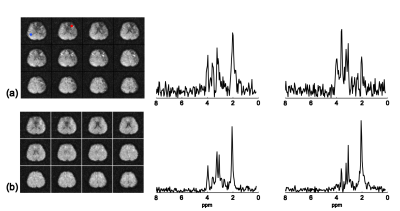
The proposed method has been evaluated using both phantom and in vivo data obtained by the SPICE technique4 on a 3T scanner with the following imaging parameters: TR/TE=260/4 ms, 1.78 ms echo-spacing, 230×230×72 mm3 FOV and 96×110×24 matrix size. The phantom is a cylindrical jar containing NaCl-doped water and nine vials of metabolite solutions. Two sets of phantom data were acquired with and without WS respectively. Figure 1 illustrates the effectiveness of the proposed method using Fourier reconstructions. Figure 2 demonstrates the performance of the proposed method by comparing SPICE reconstructions of the data with and without WS. As the results show, the proposed method can effectively remove the sideband artifacts without introducing much spectral distortion. In vivo non-WS data were also acquired from a healthy subject. The results in Fig. 3 clearly show the improved reconstruction with sideband signals removed by the proposed method.

Conclusions

This work proposes a novel method to remove the water sideband signals from 1H-MRSI data acquired without WS. This method provides a simple and effective solution to a long-standing problem in 1H-MRSI. The proposed method is expected to be useful for many non-WS 1H-MRSI studies.

Acknowledgements

This work was supported in part by the following research grants: NIH-R21-EB021013-01 and NIH-P41-EB002034.

References

1. Dong, Z. (2015). Proton MRS and MRSI of the brain without water suppression. Progress in nuclear magnetic resonance spectroscopy, 86, 65-79.

2. Barkhuijsen, H., De Beer, R., & Van Ormondt, D. (1987). Improved algorithm for noniterative time-domain model fitting to exponentially damped magnetic resonance signals. Journal of Magnetic Resonance (1969), 73(3), 553-557.

3. Ratiney, H., Sdika, M., Coenradie, Y., Cavassila, S., Ormondt, D. V., & Graveron‐Demilly, D. (2005). Time‐domain semi‐parametric estimation based on a metabolite basis set. NMR in Biomedicine, 18(1), 1-13.

4. Lam, F., Ma, C., Clifford, B., Johnson, C. L., & Liang, Z.-P. (2016). High‐resolution 1H‐MRSI of the brain using SPICE: Data acquisition and image reconstruction. Magnetic resonance in medicine, 76(4), 1059-1070.

5. Lam, F., Li, Y., Clifford, B.,Peng, X., & Liang, Z.-P. (2017). Simultaneous mapping of brain metabolites, macromolecules and tissue susceptibility using SPICE. Proceedings of ISMRM, Hawaii, USA, 1249.

Figures

Figure 1: Phantom results from the Fourier reconstruction (at lower resolution for better signal-to-noise ratio): (a)-(b) L2 integrals of the reconstructions of the data without and with water sideband removal, respectively, and (c) spectrum (imaginary part) from a representative location marked by the red dot. Note the bright-band artifacts in the L2 integral and the "bump" artifacts (marked by red circles) in the spectrum caused by water sidebands are significantly reduced by the proposed method.

Figure 2: Phantom results from the SPICE reconstruction: (a) Choline maps from the reconstruction of the data with WS, and (b)-(c) reconstruction results from the data acquired without WS and without and with sideband artifacts removal respectively, including Choline maps and spectra from two locations (marked by red and blue dots) compared to those from the reconstruction with WS. Note the proposed method has significantly reduced the sideband artifacts without introducing spectral distortion.

Figure 3: In vivo results from the SPICE reconstruction of (a) data without sideband removal, and (b) data processed by the proposed method, including N-acetylaspartate maps and representative spectra from voxels marked by the color dots. As can be seen, the severe artifacts and spectral distortion in the first reconstruction are significantly reduced by the proposed method. Note that in the previous SPICE-based methods4-5, the early echoes were discarded to avoid the sideband effects but with the proposed method, all the echoes can be utilized for reconstruction now.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
4016