3960
High-Speed Density Matrix Simulation of PRESS with A Single Editing PulseLi An1 and Jun Shen1
1National Institute of Mental Health, National Institutes of Health, Bethesda, MD, United States
Synopsis
A single spectral editing pulse incorporated into the PRESS sequence produces large Bloch-Siegert shift. The lack of a general method to quantify these shifts for spectral editing experiments has made it necessary to use a second identical editing pulse to cancel the shift. Here we describe a high-speed density matrix simulation method to accurately simulate a PRESS sequence with a single editing pulse for simultaneous detection of glutamate, glutamine, GABA, and glutathione at TE = 56 ms and 7 Tesla. To facilitate in vivo quantification, the frequency dependent Bloch-Siegert shift is accurately calculated and removed from the spectra.
INTRODUCTION
A single spectral editing pulse incorporated into the PRESS sequence can produce large Bloch-Siegert shift (1). The MEGA-PRESS method cancels this shift by adding a second identical editing pulse (2). A recently proposed full density matrix simulation technique (3) converts the time-consuming three-dimensional density matrix simulation of PRESS into three one-dimensional computation problems, shortening the computation time by orders of magnitude. Here, we applied the principle of one-dimensional projection to density matrix simulation of PRESS-based spectral editing using a single editing pulse for simultaneous detection of glutamate, glutamine, γ-aminobutyric acid (GABA), and glutathione at TE = 56 ms and 7 Tesla. The Bloch-Siegert shift as a function of chemical shift was accurately simulated and then removed from the spectra to allow spectral fitting of in vivo data acquired from the frontal cortex of the human brain.METHODS
The density matrix simulation programs were developed using the GAMMA NMR simulation C++ library (4). The simulated pulse sequence for simultaneous spectral editing of glutamate, glutamine, GABA, and glutathione is shown in Fig. 1. To digitize the 2 × 2 × 2 cm3 spectroscopy voxel, we used 200, 2000, and 200 spatial points in the x, y, and z directions, respectively. Based on the one-dimensional projection method (3), the spin density operator before the start of the first crusher gradient flanking the editing pulse was computed by summing up the 200 density matrices in the x direction. To account for frequency drift due to system instability and subject movement during the editing experiment, the rest of the spin density operator evolution was computed for 31 editing pulse frequency drift values ranging from -15 Hz to 15 Hz with one Hz increment. For each frequency drift value, the spin density operator was computed using two one-dimensional summations of the digitized density matrices, first in the y direction (2000 density matrices) and then in the z direction (200 density matrices). The free induction decay (FID) signals were then computed for each of the 31 frequency drift values. The Bloch-Siegert shift caused by the single editing pulse was computed by finding the phase shift values of simulated singlet peaks at 400 different frequencies between 0 – 4 ppm with a 0.01 ppm increment for each of the digitized spatial points in the y direction.RESULTS
Separately simulated spectra of NAA using the ideal 90° pulse and the experimentally implemented 90° pulse are displayed in Fig. 2. The two simulated spectra are practically identical, which shows that the use of the ideal 90° pulse does not cause any significant error. The Bloch-Siegert shift as a function of chemical shift when the editing pulse was applied at 2.12 ppm is plotted in Fig. 3. The Bloch-Siegert shift when the editing pulse was applied at 1.89 ppm is similar, which can be obtained by shifting the curve in Fig. 3 upfield by 0.23 ppm. Simulated spectra of NAA, glutamate, GABA, glutamine, and glutathione with editing pulse ON at 2.12 ppm are displayed in Fig. 4. Fig. 4a shows the spectra without correction of the Bloch-Siegert shift. Fig. 4b shows the spectra after the Bloch-Siegert shift was removed. The modified one-dimensional projection simulations remained very time efficient. For example, on a typical laptop computer, it took only 1.25 minutes to simulate the 4-spin NAA spectra with 31 frequency drift values of the editing pulse over the 200 × 2000 × 200 digitized spectroscopy voxel. Reconstructed spectra acquired at 7 Tesla from a 2 × 2 × 2 cm3 voxel placed in the pregenual anterior cingulate cortex (pgACC) of one healthy volunteer and the corresponding fits are displayed in Fig. 5. The MRS scan time was 4.5 min. The fits closely matched the in vivo spectra.DISCUSSION AND CONCLUSION
Keltner et al. (1) pioneered spectral editing of GABA using a PRESS-based sequence. To overcome the large Bloch-Siegert shift, they carefully chose the amplitude and duration of the editing pulse such that the Bloch-Siegert shift at 3.0 ppm became zero. As demonstrated in the current work, full density matrix simulation provides a practical way to accurately account for the Bloch-Siegert shift over the whole spectrum. The use of a single editing pulse can also shorten the echo time and provide additional freedom to design pulse sequences for simultaneously editing multiple metabolite signals.Acknowledgements
This work was supported by the intramural programs of the NIH and NIMH.References
- Keltner JR, Wald LL, Christensen JD, Maas LC, Moore CM, Cohen BM, Renshaw PF. A technique for detecting GABA in the human brain with PRESS localization and optimized refocusing spectral editing radiofrequency pulses. Magnetic Resonance in Medicine 1996;36(3):458-461
- Mescher M, Merkle H, Kirsch J, Garwood M, Gruetter R. Simultaneous in vivo spectral editing and water suppression. Nmr in Biomedicine 1998;11(6):266-272.
- Zhang Y, An L, Shen J. Fast computation of full density matrix of multispin systems for spatially localized in vivo magnetic resonance spectroscopy. Medical Physics 2017;44(8):4169-4178.
- Smith SA, Levante TO, Meier BH, Ernst RR. Computer-Simulations in Magnetic-Resonance - an Object-Oriented Programming Approach. Journal of Magnetic Resonance Series A 1994;106(1):75-105.
Figures
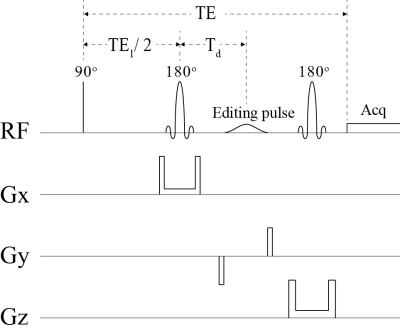
Fig. 1 Schematics
of the simulated PRESS-based pulse sequence with a single truncated Gaussian
pulse for spectral editing of glutamate, glutamine, GABA, and glutathione. TE =
56 ms, TE1 = 40 ms, Td = 15.3 ms. Editing RF pulse
setting: OFF, ON at 1.89 ppm, and ON at 2.12 ppm. The 90° excitation pulse was an ideal pulse. The two 180° refocusing pulses (duration =
8.0 ms and bandwidth = 2.0 kHz) and the editing pulse (duration = 10.0 ms and
bandwidth = 106 Hz) were actual pulses implemented on the 7 Tesla scanner.
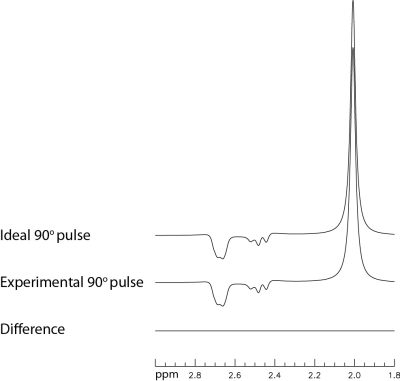
Fig. 2 Comparison of
numerically simulated spectra of NAA using the ideal 90° pulse and
the actual 90° pulse (duration = 4.5 ms and bandwidth = 3.1 kHz). The
pulse sequence had no editing pulse and used TE = 56 ms and TE1 = 40
ms.

Fig.
3
Plot of the Bloch-Siegert shift as a function of chemical shift when the
editing pulse was applied at 2.12 ppm.
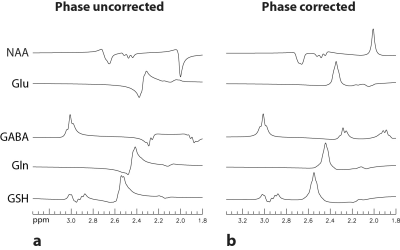
Fig. 4 Spectra
of NAA, glutamate, GABA, glutamine, and glutathione computed using the proposed
density matrix simulation method. The same concentration was used for all five metabolites.
All spectra were broadened to a singlet half-height width of 9 Hz. a. No Bloch-Siegert correction was
applied. b. The Bloch-Siegert shift was removed from the spectra.

Fig.
5
Reconstructed spectra and corresponding fits from the pregenual anterior
cingulate cortex (pgACC) of
one healthy volunteer. Bloch-Siegert phase shifts caused by the editing pulse
have been removed from both the in vivo
and fitted spectra.