Synopsis

To speed up the acquisition time of multi-dimensional magnetic resonance spectroscopy (MRS), one typical way is to sparsely acquire free induction decay (FID) data reconstruct the spectrum from the incomplete observations. Recently, a low rank Hankel matrix (LRHM) approach, that explores the sparse number of spectral peaks, has shown great ability to reconstruct the spectrum. When the data are highly undersampled, however, low intensity spectral peaks are compromised in the reconstruction. In this abstract, a weighted LRHM approach is proposed. A weighted nuclear norm is introduced to better approximate the rank constraint, and a prior signal space is estimated from the pre-reconstruction to reduce the number of unknowns in reconstruction. Results on both synthetic and real MRS data demonstrate that the proposed approach can reconstruct low intensity spectral peaks better than the state-of-the-art LRHM method.

Purpose

Method

Here we introduced a weighted nuclear norm to better approximate the rank constraint. Let $$$\mathbf{X}$$$ denote a matrix, and the weighted nuclear norm[6] is defined as below

$${{\left\| \mathbf{X} \right\|}_{\mathbf{w},*}}=\sum\limits_{s=1}^{S}{{{w}_{s}}{{\sigma }_{s}}}, \qquad (1)$$

where $$$\mathbf{w}={{\left[ {{w}_{1}},\cdots ,{{w}_{s}},\cdots ,{{w}_{S}} \right]}^{T}}$$$ includes the weight $$${{w}_{s}}\left( 1\le s\le S \right)$$$ for the $$${{s}^{\text{th}}}$$$ singular values.

The model we introduced into MRS is named as Weighted Low Rank Hankel Matrix (WLRHM)

$$\underset{\mathbf{x}}{\mathop{\text{min}}}\,{{\left\| \mathbf{Rx} \right\|}_{\mathbf{w},*}}+\frac{\lambda }{2}\left\| \mathbf{y}-\mathbf{Ux} \right\|_{2}^{2}, \qquad (2)$$

where $$$\mathbf{R}$$$ denote an operator converting the FID $$$\mathbf{x}$$$ into a Hankel matrix $$$\mathbf{Rx}$$$, $$${{\left\| \cdot \right\|}_{\mathbf{w},*}}$$$ represents the weighted nuclear norm, $$${{\left\| \cdot \right\|}_{2}}$$$ represents the $$$\ell_2$$$ norm, and $$$\lambda $$$ denotes a regularization parameter that balances the two terms.

First, the LRHM is used to obtain a pre-reconstruction result $$$\mathbf{\tilde{x}}$$$ followed by the singular value decomposition according to

$$\mathbf{R\tilde{x}}=\mathbf{\tilde{P}\tilde{\Sigma }}{{\left( {\mathbf{\tilde{V}}} \right)}^{H}}, \qquad (3)$$

where the matrix $$$\mathbf{\tilde{P}}$$$ contains the spectral frequency information of $$$\mathbf{\tilde{x}}$$$ and $$$\mathbf{\tilde{\Sigma }}$$$ consists the singular values. Then, a discriminative weight $$$\mathbf{w}={{\left[ {{w}_{1}},\cdots {{w}_{s}}\cdots ,{{w}_{S}} \right]}^{T}}$$$ is computed as follows

$${{w}_{s}}=\frac{1}{{{{\mathbf{\tilde{\Sigma }}}}_{s}}+\varepsilon },\qquad (4)$$

where $$$\varepsilon $$$ is a small constant that avoids zeros in the denominator and $$${{\mathbf{\tilde{\Sigma }}}_{s}}$$$ is the $$${{s}^{\text{th}}}$$$ singular values of $$$\mathbf{\tilde{\Sigma }}$$$.

One can see in Eq. (2) that the weighted nuclear norm minimization needs singular value decomposition iteratively. We observe that most spectral frequency components of MRS are recovered properly with LRHM. Thus, one may try to project the Hankel matrix onto these pre-estimated frequencies. In another word, $$$\mathbf{\tilde{P}}$$$ keep the same in the iterative reconstruction process. This modification potentially reduces the number of unknowns in the low rank reconstruction.

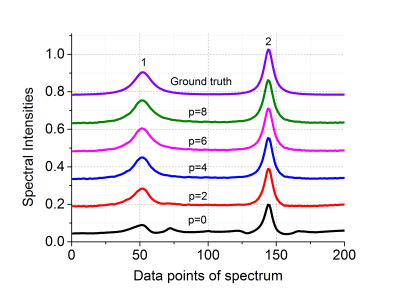
To achieve better reconstructions, both the weight $$$\mathbf{w}$$$ and matrix $$$\mathbf{\tilde{P}}$$$ are updated using WLRHM reconstruction for several times. The benefits of incorporating weights are analyzed in Fig. 1. Using the proposed approach, spectral correlations are increased for all peaks and the improvement is more obvious for low intensity peaks. More times of updating weights lead to spectral shapes more consistent to the ground truth, however, at the cost of more computation time. In the implementation, the updating times is chosen to be 4 so that reconstructed spectra are restored pretty well without paying too much extra computation time.

Results

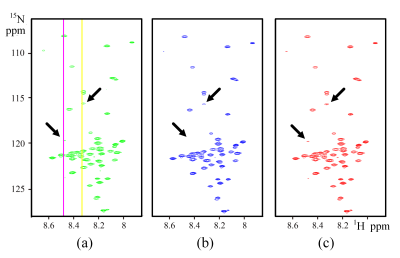
The proposed WLRHM is compared with LRHM, whose reconstruction performances are evaluated on realistic biological MRS measured from proteins [4, 7]. The 2D MRS (Fig. 2(a)) is a 1H-15N HSQC spectrum of the intrinsically disordered cytosolic domain of human CD79b protein from the B-cell receptor [7].

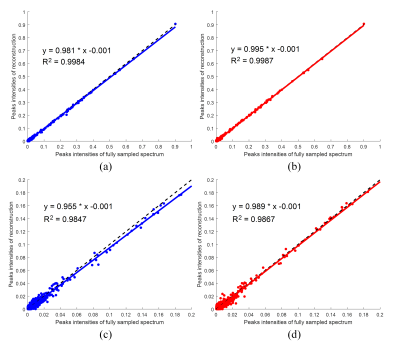
The WLRHM reconstructs the spectral peaks (Fig. 2(c)) better than the LRHM (Fig. 2(b)), particularly for the marked spectral peaks. As shown in Fig. 3, the quantitative analysis on the spectrum intensities correlation also confirms that WLRHM improve low intensity spectrum (Fig. 3(c) and (d)) although the improvement for all peaks (Fig. 3(a) and (b)) is not significant. These observations imply that the proposed method can reconstruct more consistent spectrum to the fully sampled 2D MRS.

Conclusion

Acknowledgements

References

[1] K. Kazimierczuk and V. Orekhov, Accelerated NMR spectroscopy by using compressed sensing, Angewandte Chemie International Edition, vol. 50, pp. 5556-5559, 2011.

[2] X. Qu, X. Cao, D. Guo, and Z. Chen, Compressed sensing for sparse magnetic resonance spectroscopy, in International Society for Magnetic Resonance in Medicine 18th Scientific Meeting, Stockholm, Sweden, 2010, p. 3371.

[3] X. Qu, D. Guo, X. Cao, S. Cai, and Z. Chen, Reconstruction of self-sparse 2D NMR spectra from undersampled data in the indirect dimension, Sensors, vol. 11, pp. 8888-8909, 2011.

[4] X. Qu, M. Mayzel, J. F. Cai, Z. Chen, and V. Orekhov, Accelerated NMR spectroscopy with low-rank reconstruction, Angewandte Chemie International Edition, vol. 54, pp. 852-4, 2015.

[5] J. Ying, H. Lu, Q. Wei, J. F. Cai, D. Guo, J. Wu, Z. Chen, and X. Qu, Hankel matrix nuclear norm regularized tensor completion for $$$N$$$-dimensional exponential signals, IEEE Transactions on Signal Processing, vol. 65, pp. 3702-3717, 2017.

[6] S. Gu, Q. Xie, D. Meng, W. Zuo, X. Feng, and L. Zhang, Weighted nuclear norm minimization and its applications to low level vision, International Journal of Computer Vision, vol. 121, pp. 183-208, 2017.

[7] L. Isaksson, M. Mayzel, M. Saline, A. Pedersen, J. Rosenlöw, B. Brutscher, B. Karlsson, and V. Orekhov, Highly efficient NMR assignment of intrinsically disordered proteins: Application to B-and T cell receptor domains, PLos one, vol. 8, e62947, 2013.