3872
Improved Encoding Efficiency in Sodium MRI with Zero-Gradient-Excitation Ramped Hybrid Encoding (zGRF-RHE)1Biomedical Engineering, University of Melbourne, Melbourne, Australia, 2Melbourne Brain Centre Imaging Unit, University of Melbourne, Melbourne, Australia
Synopsis
The fast signal decay in sodium MRI makes high quality image acquisition challenging. Here we enhance image quality by improving encoding time (tenc) efficiency using a special case of ramped hybrid encoding , zero-gradient-under-RF-excitation RHE (zGRF-RHE). This provides 1) gradient-free-excitation for high flip angle, non-selective excitation profiles necessitated by low signal in sodium MRI and 2) gradient ramping during deadtime for optimised tenc, to reduce T2 decay influence during acquisition. The performance of zGRF-RHE is demonstrated in simulations, phantom and in vivo experiments and improves image quality (SNR and T2 blurring). It is applicable to any centre-out trajectory design.
Introduction
Sodium MRI offers promise as a clinical imaging modality, but currently provides comparatively low image quality resulting from low MR-sensitivity and fast biexponential MR-signal decay of sodium1. The latter necessitates image acquisition with dedicated sequences enabling short encoding time (tenc). Typically applied UTE sequences are, however, limited due to finite gradient slew rates, and zTE tenc improvements are not readily achievable in sodium MRI due to B1 limitations2-4. Finite transmit/receive switching time (deadtime) introduces an additional hardware constraint on fast sampling onset (~40-100μs on clinical systems).
This work proposes a special case of ramped hybrid encoding (RHE)5 for an optimisation of tenc under low sodium MR-signal conditions. Zero-gradient-excitation (zGRF)-RHE (Figure 1) uses hybrid encoding and provides 1) gradient-free excitation for high flip angle, non-selective excitation profiles and 2) gradient ramping during deadtime for tenc optimisation to reduce T2 signal decay influence during acquisition.
Methods
Acquisition
Imaging was conducted on a research 7T MRI scanner (Siemens Healthcare, Erlangen, Germany) with a transmit/receive dual-tuned 1H-23Na head coil (QED, USA) using a custom-built 3D-radial sequence. Simulations and experiments in phantoms and in vivo brain were performed with standard UTE and zGRF–RHE sequence setups. Simulation and imaging parameters were: FA=90°, TE=0.3ms, TR=160ms, resolution=(3.1mm)3, FOV=20cm, TRO=2-8ms, 8000 projections. Central k-space in zGRF-RHE was acquired through single point measurements at the minimum achievable TE=0.3ms.
Phantom
Vials with varying diameter (28, 14 and 6mm) and 3%-agar saline concentrations (30 and 45mM) were submerged in distilled water. Experiments at TRO=2,4,6 and 8ms were repeated 8 times for statistical SNR analysis.
In vivo
Human in vivo acquisitions were performed on a healthy female volunteer with TRO=2ms - TAUTE=21min20sec, TAzGRF-RHE=21min24sec. Additionally, a proton-based FLASH image was measured with TR=11ms, TE=3.06ms, FA=14°, resolution=(1mm)3, TA=6min12sec.
Reconstruction
Images were reconstructed offline via Kaiser-Bessel re-gridding in MATLAB with an oversampling factor of 1.5. Radial and single point measurements were combined for zGRF-RHE reconstruction. An iterative density compensation was applied6. A Hann-filter was applied to radial rawdata to reduce Gibbs ringing.
Results
Figure 2a illustrates the modulation transfer function (MTF) and tenc for TRO=2ms and TRO=8ms under biexponential decay (T2short=1.5ms, T2long=20ms; 0.6 and 0.4 signal fractions, respectively). Figure 2c depicts the required tenc across k-space. For any TRO, zGRF-RHE traverses through k-space quicker than UTE thanks to gradient pre-ramping leading to better MTF characteristics and a shortened sampling duration. Single point measurements in zGRF-RHE fixate tenc in k-space center. Given the smaller gradients for longer TRO the central k-space gap is smaller.
Figure 2b shows simulated profile reconstructions for UTE and zGRF-RHE at TRO=2ms and TRO=8ms. Quicker sampling results in stronger signal in zGRF-RHE. The finite difference illustration in Figure 2d emphasises sharper edges due to reduced T2 blurring in zGRF-RHE, particularly at shorter TRO.
Figure 3a depicts the phantom setup, UTE and zGRF-RHE images at TRO=2ms are shown in Figure 3c. Contour lines from normalised images illustrate sharper edges between vials in zGRF-RHE measurements and a better delineation of small details (red arrows). The mean line profile across the central slice of 14mm phantoms in TRO=2ms and TRO=8ms experiments is plotted in Figure 3b. At the same readout bandwidth, zGRF-RHE achieves higher signal due to improved tenc. Figure 3d depicts the mean edge sharpness in 14mm phantoms. Edges were measured between the central voxel of the vial and background voxel to either side. Edge definition improves with shorter TRO. Across all TRO, zGRF-RHE shows mean edge enhancements for both sodium concentrations.
SNR results calculated from a central region in 28mm vials are displayed in Figure 4. An average SNR increase of up to 4.8% was observed for zGRF-RHE across all TRO with significant gain at longer TRO. Concomitant improvements in contrast-to-noise ratio (CNR) between 30 and 45mM vials were found.
Figure 5a depicts cross sections in in vivo experiments. zGRF-RHE shows better detail around the brain stem. A FLASH-based CSF mask was registered to UTE and zGRF-RHE images using FSL. Figure 5b shows three consecutive slices of CSF segmentation through the ventricles with contour masks of normalised sodium images superimposed. zGRF-RHE measurements reveal a better delineation of the lateral ventricles.
Discussion and Conclusion
This work introduces zGRF-RHE for a readout-independent improvement of tenc efficiency in sodium MRI under preserved non-selective high flip angle excitations. Shortened tenc results in improved image quality as evidenced by increased SNR and reduced T2 blurring. While this work investigated radial acquisition schemes, tenc optimisation with hybrid encoding and gradient pre-ramping is applicable to any centre-out trajectory design7-10.Acknowledgements
We acknowledge the facilities, and the scientific and technical assistance of the Australian National Imaging Facility at the Melbourne Brain Centre Imaging Unit. The Australian National Imaging Facility is funded by the Australian Government NCRIS program.
The work was also supported by a research collaboration agreement with Siemens Healthcare.
Jon Cleary is funded by a University of Melbourne McKenzie fellowship. Brad Moffat is supported by the Australian National Imaging Facility (NIF).
References
1. Thulborn KR. Quantitative sodium MR imaging: A review of its evolving role in medicine. Neuroimage 2016.
2. Balcom BJ, Macgregor RP, Beyea SD, Green DP, Armstrong RL, Bremner TW. Single-Point Ramped Imaging with T1 Enhancement (SPRITE). J Magn Reson A 1996;123(1):131-134.
3. Romanzetti S, Halse M, Kaffanke J, Zilles K, Balcom BJ, Shah NJ. A comparison of three SPRITE techniques for the quantitative 3D imaging of the 23Na spin density on a 4T whole-body machine. J Magn Reson 2006;179(1):64-72.
4. Heid O, Deimling, M. Rapid Single Point (RASP) Imaging. 1995; Nice, France. p 684.
5. Jang H, Wiens CN, McMillan AB. Ramped hybrid encoding for improved ultrashort echo time imaging. Magn Reson Med 2016;76(3):814-825.
6. Zwart NR, Johnson KO, Pipe JG. Efficient sample density estimation by combining gridding and an optimized kernel. Magn Reson Med 2012;67(3):701-710.
7. Boada FE, Gillen JS, Shen GX, Chang SY, Thulborn KR. Fast three dimensional sodium imaging. Magn Reson Med 1997;37(5):706-715.
8. Lu A, Atkinson IC, Claiborne TC, Damen FC, Thulborn KR. Quantitative sodium imaging with a flexible twisted projection pulse sequence. Magn Reson Med 2010;63(6):1583-1593.
9. Nagel AM, Laun FB, Weber MA, Matthies C, Semmler W, Schad LR. Sodium MRI using a density-adapted 3D radial acquisition technique. Magn Reson Med 2009;62(6):1565-1573.
10. Riemer F, Solanky BS, Stehning C, Clemence M, Wheeler-Kingshott CA, Golay X. Sodium ((23)Na) ultra-short echo time imaging in the human brain using a 3D-Cones trajectory. MAGMA 2014;27(1):35-46.
Figures
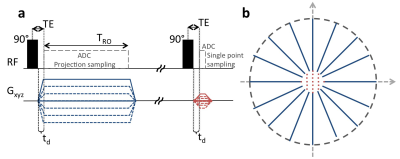
Figure 1: Radial zero-Gradient-Excitation Ramped Hybrid Encoding (zGRF-RHE).
Sequence Diagram (a) and 2D illustration of hybrid k-space encoding scheme (b). Gradient-free excitation is followed by an immediate gradient ramping, data sampling commences after deadtime td. Central k-space is measured separately as single points with the same gradient pre-ramping condition.
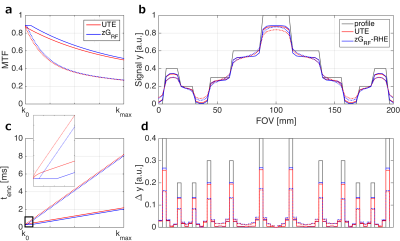
Figure 2: UTE and zGRF-RHE sequence characteristics comparison.
Left: Modulation transfer function (MTF) (a) and encoding time (tenc) (c) over k-space readout. Zoomed-in window illustrates reduced encoding efficiency during ramp up in standard UTE (red). Solid line indicates 2ms TRO, dashed line shows 8ms TRO.
Right: Profile simulation (b) and edge definition analysis (d). (b) Black line illustrates simulated profile, red line shows standard UTE, blue line indicates zGRF-RHE results for TRO=2ms (solid) and TRO=8ms (dashed). (d) indicates finite differences of original profile and simulated reconstructions.
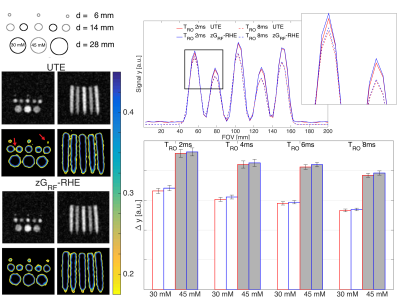
Figure 3: Phantom experiment.
Left: Phantom setup (a) and reconstructed images at TRO=2ms (c) from UTE and zGRF-RHE experiments. Upper rows show reconstructed images at the native FOV, lower rows display edge characteristics through zoomed in contour lines of normalised images.
Right: Mean line profiles (b) through 14mm vials at TRO=2ms (solid lines) and TRO=8ms (dashed lines) in UTE (red) and zGRF-RHE (blue). Mean edge sharpness (d), i.e. finite difference between central voxel and neighbouring background voxel, in 14mm vials at 45mM (grey) and 30mM (white) concentrations across TRO. Red bar contour indicates UTE, blue bar contour shows zGRF-RHE edges.
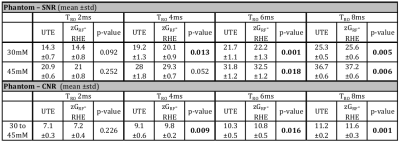
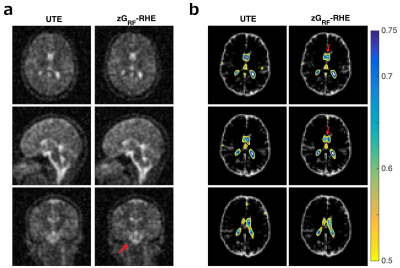
Figure 5: In vivo experiment.
(a) Cross sections through matched slices in in vivo experiments at TRO=2ms UTE and zGRF-RHE. zGRF-RHE shows sharper details around the brain stem. (b) Three consecutive transverse slices of CSF masks with contour lines of normalised UTE and zGRF-RHE at TRO=2ms. Sharper delineation of lateral ventricles in zGRF-RHE (red arrows).