3861
Cross-validated full-field of view MRSI using a new spatial lipid extraction technique and HSVD and PG algorithms in the human brain.1Hoglund Brain Imaging Center, University of Kansas Medical Center, Kansas City, KS, United States, 2Neurology, University of Kansas Medical Center, Kansas City, KS, United States, 3Department of Molecular & Integrative Physiology, University of Kansas Medical Center, Kansas City, KS, United States
Synopsis
Reliable 1H MRS measurement in the brain is challenging due to strong lipid signals as high as two orders of magnitude stronger than metabolites. We propose a new spatial-domain post processing technique to extract the lipid signal and compare our method with the HSVD and PG algorithms applied to full field of view (FOV) MRSI data (no lipid nulling, no outer volume suppression). Results of lipid removal were assessed visually and by spectral quantification of MRSI voxels for N=9 subjects. Our method outperformed HSVD and PG and achieved reliable full-FOV MRSI, promising to reach the maximum potential of whole-brain MRSI.
Target Audience
Scientists and technologists
interested in advanced in vivo
1H MRS methods to measure neurochemicals in the whole brain to
enable region-specific quantitative analysis of metabolic activity.Introduction
Subcutaneous lipids pose a
major obstacle in MRSI of the brain due to their high concentrations (over 100×
those of metabolites), broad spectral linewidth (short T2*) and phase
distortions resulting from poor shimming in the extracranial regions, and the
broad point spread function (PSF) of MRSI. Inversion recovery (IR) nulling and outer
volume suppression (OVS) have been necessary to suppress extracranial lipids in
MRSI to achieve accurate quantification of neurochemicals. Recently, lipid removal
has been achieved through post processing by taking advantage of high
resolution imaging or chemical shift spectral prior information to
model the lipid signal components [1-8]. We have developed a spatial
post-processing reconstruction method, dubbed Fast Lipid Pattern
Estimation and Removal (FLIPPER), with minimal complexity and computational
demand compared to previous approaches, that enables quantification of all MRSI
voxels over the brain from full-field of view (FOV) MRSI. The purpose of this
study was to examine the performance of our proposed method in vivo and
compare it with the well-known spectral HSVD [9] and spatial
Papoulis-Gerchberg (PG) [10] algorithms.Theory
A complex-valued image of k-space data can be defined as $$ p_R
(x,y)=1/N\sum_{n=1}^Ns_n e^{j2\pi (k_{n_x} x+k_{n_y} y)} {}{}(1)$$
where $$$ k_{n_x},k_{n_y} $$$ are the elements of phase encoding vectors
$$$k_n$$$, and $$$x,y$$$ are spatial coordinates corresponding to a
zero-padded uniform k-space. In this view, the lipid signal components
of $$$ \textbf{s} $$$ produce ringing artifacts associated with the
point spread function (PSF). Conversely, the contribution to $$$
\textbf{s} $$$ by an image $$$ c(x,y) $$$ with unrestricted k-space is
given by $$s_n=\sum_{m=1}^M c(x_m,y_m) e^{-j2\pi(k_{n_x}x_m+k_{n_y}y_m)}
(2)$$where $$$ x_m,y_m $$$ are the image coordinates. This can be
expressed by a matrix relation $$ \textbf{s}=G\textbf{c} (3)$$
In MRSI,
$$$ \textbf{s} $$$ contains lipid (extracranial) and metabolite
(intracranial) contributions $$$ \textbf{s}=\textbf{s}_l+\textbf{s}_m
$$$. The error of a fit to $$$ \textbf{s}$$$ can be minimized in the
least squares (LS)
sense including a regularization parameter,
$$ \underset{c}{\operatorname{arg min}} ||\textbf{s}-G\textbf{c}||^2 +
\lambda||R\textbf{c}||^2 (4)$$
The key to
improving the performance of Eq. 4 is to tailor the basis functions to
address
signal leakage between isolated domains in tandem with the regularized
inverse.
We propose a simple, physical rationale to set up and solve the problem
of Eq.
3. Finally, we subtract the reconstructed lipid signal from original
MRSI data
prior to lineshape fitting based quantitation.Methods
All subjects were consented according to institutional
review board approved protocols. All MR measurements were perfomed on a 3
T scanner
(Skyra, Siemens) using a 32 channel head receive coil. MRSI data were
acquired
using a semi-LASER [11] sequence with frequency drift correction using
an interleaved reference [12] (TE/TR=35/1600ms, matrix=16×16, FOV=20cm),
with the
slab positioned across the prefrontal to parietal lobes. High resolution
imaging was performed using a sagittal MPRAGE sequence with 176×256×256
dimensions. Subcutaneous lipid segmentation was performed by in-house
routines
(Matlab, Natick, MA) on image slices resampled to 128×128. The
extracranial lipid
signal was isolated from raw MRSI data using the theory described above,
before
coil combination. The HSVD and PG algorithms were implemented as
previously
desribed [9, 10, 13], with the HSVD poles residing away from
metabolites of interest, i.e., <1.9 ppm, and number of poles for
optimal removal and support size that yielded satisfactory results with
reasonable computation time. For the PG algorithm, 15 iterations were
applied
using the same lipid mask. Spectral quantification was performed on
lipid-subtracted data after coil summation using LCModel [14]
on all MRSI voxels with ≥50% tissue fraction.Results and Discussion
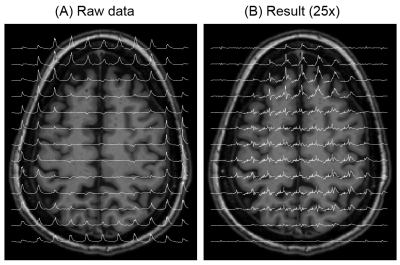
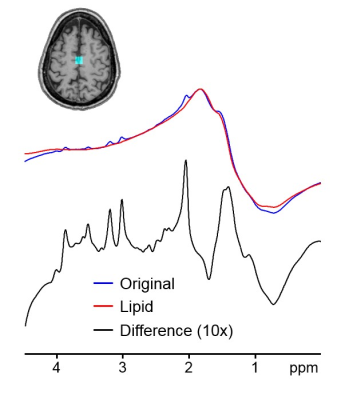
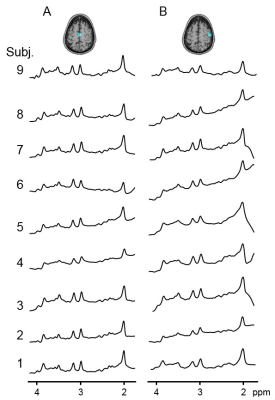
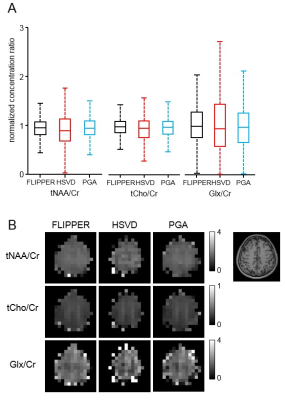
Our proposed method could isolate and remove the large nuisance lipid signals originating from the scalp in full-FOV MRSI (Fig. 1) without a loss of neurochemical signals originated from the brain (Fig. 2). The lipid removal was consistent in all nine subjects for both voxels located in the middle and at the edge of the brain (Fig. 3). Lipid removal performance of the proposed method was superior to that of the spectral HSVD and PG algorithm as indicated by the higher number of voxels that could pass spectral quality criteria and smaller variance of quantified neurochemical concentrations (Fig. 4). In conclusion, we have demonstrated a successful removal of interfering lipid signals from MRSI data acquired without any lipid attenuating strategies using a new lipid removal algorithm. The proposed algorithm could be readily extended to 3-dimensional MRSI data sets and is promising approach to extend neurochemical measurement to the previously inaccessible functionally important area, e.g., outer cortical areas.Acknowledgements
The Hoglund Brain Imaging Center is supported by the NIH (S10RR029577) and the Hoglund Family Foundation.References
[1] C. Ma, F. Lam, C. L. Johnson, and Z. P. Liang, “Removal of nuisance signals from limited and sparse 1H MRSI data using a union-of-subspaces model,” Magn Reson Med, vol. 75, no. 2, pp. 488-97, Feb, 2016.
[2] J. Lee, and E. Adalsteinsson, "Iterative CSI Reconstruction with High-Resolution Spatial Priors for Improved Lipid Suppression." p. 965.
[3] B. Bilgic, B. Gagoski, T. Kok, and E. Adalsteinsson, “Lipid suppression in CSI with spatial priors and highly undersampled peripheral k-space,” Magn Reson Med, vol. 69, no. 6, pp. 1501-11, Jun, 2013.
[4] R. Eslami, and M. Jacob, “Robust reconstruction of MRSI data using a sparse spectral model and high resolution MRI priors,” IEEE Trans Med Imaging, vol. 29, no. 6, pp. 1297-309, Jun, 2010.
[5] J. Tsao, “Extension of finite-support extrapolation using the generalized series model for MR spectroscopic imaging,” Ieee Transactions on Medical Imaging, vol. 20, no. 11, pp. 1178-1183, Nov, 2001.
[6] F. Lam, and Z. P. Liang, “A subspace approach to high-resolution spectroscopic imaging,” Magn Reson Med, vol. 71, no. 4, pp. 1349-57, Apr, 2014.
[7] Y. Liu, C. Ma, B. A. Clifford, F. Lam, C. L. Johnson, and Z. P. Liang, “Improved Low-Rank Filtering of Magnetic Resonance Spectroscopic Imaging Data Corrupted by Noise and B(0) Field Inhomogeneity,” IEEE Trans Biomed Eng, vol. 63, no. 4, pp. 841-9, Apr, 2016.
[8] Q. Ning, C. Ma, F. Lam, and Z. P. Liang, “Spectral Quantification for High-Resolution MR Spectroscopic Imaging with Spatiospectral Constraints,” IEEE Trans Biomed Eng, Jul 27, 2016.
[9] H. Barkhuijsen, R. Debeer, and D. Vanormondt, “Improved Algorithm for Noniterative Time-Domain Model-Fitting to Exponentially Damped Magnetic-Resonance Signals,” Journal of Magnetic Resonance, vol. 73, no. 3, pp. 553-557, Jul, 1987.
[10] A. Papoulis, “New Algorithm in Spectral Analysis and Band-Limited Extrapolation,” Ieee Transactions on Circuits and Systems, vol. 22, no. 9, pp. 735-742, 1975.
[11] T. W. Scheenen, D. W. Klomp, J. P. Wijnen, and A. Heerschap, “Short echo time 1H-MRSI of the human brain at 3T with minimal chemical shift displacement errors using adiabatic refocusing pulses,” Magn Reson Med, vol. 59, no. 1, pp. 1-6, Jan, 2008.
[12] T. Lange, M. Zaitsev, and M. Buechert, “Correction of frequency drifts induced by gradient heating in 1H spectra using interleaved reference spectroscopy,” J Magn Reson Imaging, vol. 33, no. 3, pp. 748-54, Mar, 2011.
[13] C. I. Haupt, N. Schuff, M. W. Weiner, and A. A. Maudsley, “Removal of lipid artifacts in 1H spectroscopic imaging by data extrapolation,” Magn Reson Med, vol. 35, no. 5, pp. 678-87, May, 1996.
[14] S. W. Provencher, “Automatic quantitation of localized in vivo 1H spectra with LCModel,” NMR Biomed, vol. 14, no. 4, pp. 260-4, Jun, 2001.
Figures