3847
Whole Brain 5mm-isotropic 3D 1H-FID-MRSI accelerated with Compressed-Sensing SENSE1Radiology and Medical Informatics, University of Geneva, Geneva, Switzerland, 2Institute of Bioengineering, École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland
Synopsis
Proton FID-MRSI sequence was implemented in 3D to measure metabolite distributions over whole brain up to 5mm-isotropic resolution. MRSI dataset was reconstructed through a Low-Rank-TGV model enabling Compressed-sensing SENSE acceleration. Acceleration performance was assessed quantitatively on a-posteriori 6.6mm-isotropic dataset showing good agreement up to a factor 2. As proof of concept, metabolite images of a 5mm-isotropic dataset accelerated by a factor 2 were acquired and reconstructed.
Introduction
Proton - Free induced decay - magnetic resonance spectroscopic imaging (1H-FID-MRSI) method permits to detect metabolic profiles across the whole brain slices in 2D acquisition at high resolution[1-3]. This state-of-the-art method is a promising candidate for the realization of 3D isotropic metabolic profiles. The metabolite signal acquired at ultra-short echo time is unaffected by the relaxation of strongly J-coupled metabolites. The technique is therefore an excellent choice for unbiased quantification of the metabolite distribution. TR and acquisition time can be reduced considerably by using the Ernst flip angle. To allow coverage of the whole brain parenchyma, no in-plane volume selection is included. We used Lipid-Suppression by spectral orthogonality[3-5] to cope with skull lipid leakage. In clinical setting (3T), metabolic signal-to-noise of high-resolution (voxel~0.1ml) acquisition could be too low for reliable quantification. The long acquisition time in 3D might be a strong limitation too. However, using partial separability of the signal[6] and TGV reconstruction[7], MRSI dataset can be efficiently denoised. Also, following a random k-space sampling combined with known coil-sensitivity profiles, the acquisition can be accelerated with Compressed-sensing SENSE. This research aims to optimize both denoising and acceleration of high-resolution 3D FID-MRSI covering the whole brain. The performance of the technique is assessed on metabolite images and their respective Cramer-Rao-lower-bound (CRLB) values.
Method
Sequence
A volume selective 3D FID-MRSI[1] sequence including WET water suppression was designed and implemented. The volume selective excitation pulse of 0.9ms was optimized with a Shinnar-Le Roux algorithm reaching a 9.5kHz bandwidth. Phase-encoding duration was shortened to reach a TE of 0.7ms and the FID signal was acquired with 1024 points at 4kHz sampling rate leading to a TR of 370ms. Considering a maximum metabolite T1 value of 1300ms, the Ernst angle for the excitation pulse was 40 degree. To determine the coils sensitivity profiles, water signal was acquired consecutively with the body coil and the head phased-array coil and with the same sequence but with a TR of 31ms, 48 FID points and a 10 degree flip angle.
Experiment
Healthy volunteers’ data were acquired at 3T (Prisma/Siemens/Erlangen/Germany) with 64-channel receiver head coil. Structural images were acquired with 3D-T1-weighted MPRAGE sequence. 3D-FID-MRSI was planned on 210x210x105mm3 FOV and a 88mm thick slab excitation. Two encoding schemes were experimented: 1. full Low-Resolution scheme consisting of 32x32x16 elliptical encoding and 6.6x6.6x6.6mm3 resolution requiring 39min acquisition time; 2. sparse High-Resolution scheme with a 40x40x20 k-space matrix randomly filled up to 50% (acceleration factor 2) resulting in 5.3x5.3x5.3mm3 resolution that required 40min for acquisition
Lipid Suppression and Low-Rank TGV Reconstruction
Based on a skull mask made on MPRAGE structural images, a projection onto the lipid temporal subspace, $$$P^L$$$ was defined and apply on acquired MRSI dataset, $$$S(\mathbf{k},t)$$$ to remove the lipid signal by spectral orthogonality [4,5]:$$S_{free}(\mathbf{k},t)=\int(\boldsymbol{1}-P^{L}(t,t'))S(\mathbf{k},t')dt'$$We apply a Low-Rank approximation[6] on the lipid-free signal in real-space:
$$S_{free}(\mathbf{r},t)=\sum_{c=1}^{N_C}U_c(\mathbf{r})V_c(t)$$The Low-Rank decomposition highlights the spatial-spectral features while efficiently denoising the MRSI dataset[6] through a TGV reconstruction model[7]: $$\mathbf{U}(\mathbf{r}),\mathbf{V}(t)=\arg\min_{\mathbf{U},\mathbf{V}}\:\:\left\|S_{free}( \mathbf{k},t)-\mathcal{FSB}\{\mathbf{U}(\mathbf{r})\mathbf{V}(t)\}\right\|^2_2+\lambda\:TGV^2(\mathbf{U}(\mathbf{r}))$$
where $$$\mathcal{B}$$$, is the B0 inhomogeneity operator, $$$\mathcal{S}$$$, the coil-sensitivity profiles and $$$\mathcal{F}$$$, the Fourier encoding. The presented model allows for Compressed-sensing SENSE acceleration[8,9] if the k-space is sparsely and randomly sampled.
Quantification and comparison
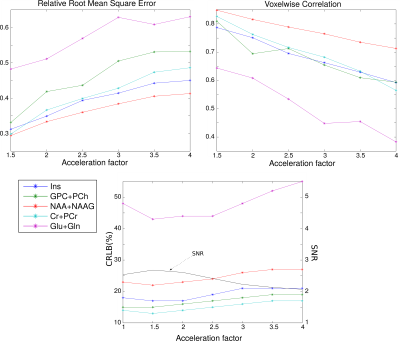
The reconstructed MRSI dataset was quantified using LCModel[10] . The full Low-Resolution dataset was a-posteriori undersampled at various acceleration factors (AF): {1.5;2;2.5;3;3.5;4} for comparison using CRLB of tNAA, tCre, Cho, Ins and Glx, SNR, relative root mean square error (RRMSE) and voxelwise correlation (VC). Eventually, an example of metabolite profiles of sparse High-Resolution acquisition are shown.
Results
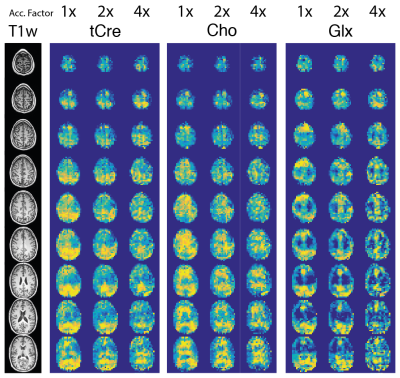
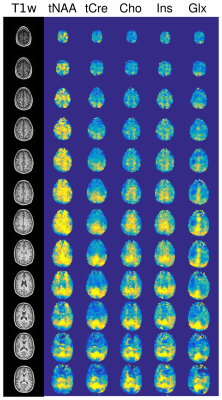
On Fig.1 acceleration of full Low-Resolution dataset by a factor 2 shows good qualitative results, factor 4 is strongly distorted. Fig.2 shows the quantitative comparison between AF. RRMSE and VC coefficients exhibit clearly the quality loss in metabolite distribution observed in Fig.1 and seem to follow $$$\sqrt{AF}$$$ or $$$1/\sqrt{AF}$$$ as expected. The Cramer-Rao Lower Bound (CRLB) and the Signal-to-Noise Ratio (SNR) are contrarily rather stable and are less efficient indicators of the images quality. These results suggest that high Compressed-sensing acceleration affects mostly the spatial distribution rather than the spectral quality. On Fig.3, results of sparse High-Resolution acquisition are shown.
Discussion
We presented preliminary data of whole brain 3D-FID-MRSI. Although whole brain 3D MRSI can already be performed with EPSI techniques[11], the methodology presented acquires data at ultra-short TE (<1ms) and with high spectral resolution (4Hz/point). The Compressed-sensing SENSE acceleration permits to produce high resolution metabolite images within a reasonable acquisition time. Future developments will be focused on optimization of B0 fieldmap corrections. In addition, we will explore k-space under-sampling pattern performance in terms of RRMSE and VC.Acknowledgements
No acknowledgement found.References
[1] Henning, A., Fuchs, A., Murdoch, J.B. and Boesiger, P. (2009). Slice-selective FID acquisition, localized by outer volume suppression (FIDLOVS) for (1)H-MRSI of the human brain at 7 T with minimal signal loss. NMR Biomed 22, 683-696.
[2] Nassirpour, S., Chang, P., Henning, A. (2017). High and ultra-high resolution metabolite mapping of the human brain using 1H FID MRSI at 9.4T. NeuroImage
[3] Hangel, G., et al. (2016). Ultra-high resolution brain metabolite mapping at 7 T by short-TR Hadamard-encoded FID-MRSI. NeuroImage
[4] Bilgic, B., Gagoski, B., Kok, T. and Adalsteinsson, E. (2013) Magn Reson Med 69, 1501-1511
[5] Klauser, A., Van De Ville, D. ,Lazeyras, F. . Low-Rank TGV Reconstruction of High-Resolution 1H-FID-MRSI of Whole Brain Slices. (2017) ISMRM 25th Annual Meeting, preceeding #5517
[6] Nguyen, H.M., Peng, X., Do, M.N. and Liang, Z. (2013). Denoising MR spectroscopic imaging data with low-rank approximations. IEEE Trans Biomed Eng 60, 78-89.
[7] Kasten, J., Lazeyras, F., & Van De Ville, D. (2013). Data-Driven MRSI Spectral Localization Via Low-Rank Component Analysis. Medical Imaging, IEEE Transactions on, 32(10), 1853–1863.
[8] Liang, D., Liu, B., Wang, J., & Ying, L. (2009). Accelerating SENSE using compressed sensing. Magnetic Resonance in Medicine, 62(6), 1574–84. https://doi.org/10.1002/mrm.22161
[9] Otazo, R., Kim, D., Axel, L., & Sodickson, D. K. (2010). Combination of compressed sensing and parallel imaging for highly accelerated first-pass cardiac perfusion MRI. Magnetic Resonance in Medicine, 64(3), 767–776. https://doi.org/10.1002/mrm.22463
[10] Provencher, S.W. (1993). Estimation of metabolite concentrations from localized in vivo proton NMR spectra. Magn Reson Med 30, 672-679.
[11] Lecocq, A., Le Fur, Y., Maudsley, A. A., Le Troter, A., Sheriff, S., Sabati, M., … Ranjeva, J.-P. (2015). Whole-brain quantitative mapping of metabolites using short echo three-dimensional proton MRSI. Journal of Magnetic Resonance Imaging, 42(2), 280–289.
Figures