3844
Fast Irregular MRSI spiral acquisition for sparse spectra. Application to 31P MRSI in muscles.1Univ Lyon, UJM-Saint-Etienne, INSA, CNRS UMR 5520, INSERM U1206, CREATIS, F-42023, SAINT-ETIENNE, France, Lyon, France, 2Siemens Healthineers, Saint-Denis, France, 3Université de Lyon, INSA-Lyon, Université Claude Bernard Lyon 1, UJM-Saint Etienne, CNRS, Inserm, CREATIS UMR 5220, U1206, Lyon, France
Synopsis
Magnetic resonance spectroscopic imaging (MRSI) has multiple interests in clinical practice but it faces quite long acquisition time in practice which limits its use in a clinical environment. In this work, a new fast Magnetic Resonance Spectroscopic image acquisition method, inspired by Compressed Sensing using the a priori known sparse support of the metabolites chemical shift, is introduced and evaluated based on a k-t space spiral sampling. In the proposed method, the spatial and temporal interleaves are both taken in consideration during the implementation, in order to reach an even faster acquisition. This method has been evaluated using real in vivo 31P data.
INTRODUCTION
MRSI is a way to evaluate the concentration of metabolites of interest in the body both in the spectral and spatial dimension. In [5], we introduced a new fast acquisition method using a spiral k space sampling, and based on an a priori known spectrum support to select a times samples set to acquire. The FID time samples to acquire are selected thanks to the Sequential Backward Selection (SBS) algorithm [3]. In this work, we aim to extend this method. Spatial and spectral interleaves of the multiple spirals in the k-t space are taken in consideration. The method has been evaluated using real in-vivo 31P data, to prove the feasibility of the proposed approach.
METHODS
Spiral k-space
sampling uses successive time varying gradients. To sufficiently
cover the kx-ky space, it is often necessary to do spatial interleaves
which depend on the length of a spiral, the desired spatial
resolution and the MRI machine system gradient commutation and
amplitude limitations.
It is also necessary to do temporal interleaves in MRSI, given the length of a spiral and the desired FID signal temporal resolution, in order to acquire all the required temporal points.
Our method is characterized by:
1) instead of
sampling the full k-space at each time point for Nspat spatial interleaves, Nspat k-subspaces are sampled with spirals
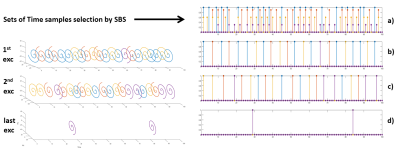
2) instead of sampling the full t-space, we subsample it thanks to the SBS algorithm calculated for an a priori known spectrum support
3) different sets of time samples are selected with different initializations of SBS for each spatial interleave.
Each set of time
samples will then correspond to a k-t subspace. Each time sample is now acquired with a spiral covering a kx-ky subspace where each set of time
samples will have a spiral design rotated from one to another,
corresponding to the spatial interleaves.
After each Repetition Time (TR), a train of spirals, of different k-subspaces, is launched in order to acquire the predefined number of points, including all the sets of time samples. (Fig. 1)
Once each k-t subspace is acquired, a LS reconstruction (Fig. 2) is performed to reconstruct the spectral support for each k-t subspace, which leads as many k-f subspaces. Then, we construct the full k-f space formed with the union of all the k-f subspaces generated. Finally, a regridding algorithm is used to interpolate the k-f space into a Cartesian grid and then reconstruct the spatial dimension.
This method has been evaluated on 31P MR spectroscopy data acquired on a Siemens Prisma 3T MRI machine. The spiral acquisition has been simulated from a cartesian acquisition, matrix size of 32x32, NA=2 [4]. Three methods have been compared: A) the conventional spiral sampling method in MRSI, B) SBS based irregular sampling for spiral trajectories [5,6] and C) the new proposal: SBS based irregular sampling coupled with spatial and temporal interleaves multiplexing. A reduction factor of 4 has been used for the time samples selection, 4 spatial interleaves and 4 temporal interleaves. Spirals length time are 1ms, in order to reach a temporal resolution of 0,25ms and a matrix size of 32x32 for a 200x200mm2 of FOV. The acquisition window is of 256ms, and the TR is of 2s.
RESULTS
The anatomic image and the in-vivo 31P acquired spectrum are represented in Fig. 3. Fig. 4 shows the in-vivo 31P image data, acquired with a conventional phase-phase encoding method, the used phantom for our simulation based on the in vivo image, and the reconstructed image with our algorithm. Fig. 5 shows the magnitude of the reconstructed 31P spectrum for method B and C for a voxel in the left ellipse. In a noise free acquisition the Signal to Reconstructed Error Ratio (SRER) were respectively 25.8 dB for method A, 24.9 dB for method B and 21.5 dB for method C for a pixel in the left ellipse. For a noisy acquisition (sigma=10%PCr), the results are: 23.6dB (A) 19.8dB (B) and 17.5 dB (C). For A), the minimum acquisition time is Tacqu = 32s. The gain in terms of acquisition is, compared to A), of 2 for B) and 2.3 for C).CONCLUSION
A new MRSI fast acquisition strategy is proposed by exploiting the irregular sampling of the spectroscopic dimension to lower the acquisition time using both spatial and spectral interleaves. We showed that we were able with this new method to reduce the scan time which represents an additional contribution in the context of fast MRSI acquisition and will be studied in the future in dynamic 31P/13C MRSI acquisition [7,8].Acknowledgements
This work has been supported by Siemens Healthineers and the LABEX PRIMES (ANR-11-LABX-0063), program ”Investissements d’Avenir” (ANR-11-IDEX-0007).References
1. Posse, S., et al., MR spectroscopic imaging: principles and recent advances. Journal of magnetic resonance imaging : JMRI, 2013. 37(6): p.1301-25.
2. Adalsteinsson, E., et al., Volumetric spectroscopic imaging with spiral-based k-space trajectories. Magnetic Resonance in Medicine, 1998.39(6): p. 889-898.
3. Reeves, S.J. and L.P. Heck. Selection of observations in signal reconstruction. IEEE Trans. Signal Proc. 1995; 43: 788-791
4. J. Fessler, Image Reconstruction Toolbox, https://web.eecs.umich.edu/~fessler/code
5. Karkouri, J. et al., Irregular spiral acquisition for compressive sensing in MRSI, ISMRM 2017
6, Karkouri, J et al., Time samples selection in spiral acquisition for sparse magnetic resonance spectroscopic imaging, IEEE ICIP 2017
7. Valkovic, Ladislav, CHMELÍK, Marek, MEYERSPEER, Martin, et al. Dynamic 31P–MRSI using spiral spectroscopic imaging can map mitochondrial capacity in muscles of the human calf during plantar flexion exercise at 7 T. NMR in Biomedicine, 2016, vol. 29, no 12, p. 1825-1834.
8. Wiesinger, F., Weidl, E., Menzel,
M. I., Janich, M. A., Khegai, O., Glaser, S. J., ... &
Schulte, R. F. (2012). IDEAL spiral CSI for dynamic metabolic MR
imaging of hyperpolarized [1‐13C] pyruvate. Magnetic resonance
in medicine, 68(1), 8-16.
Figures