3842

Arbitrary Variable Density (AVD)-GRAPPA Enabled EPSI of Short-echo 3D H1-MRSI
Maryam Vareth1,2, Yan Li1, Misung Han1, Marram P. Olson1, Jason Crane1, Sarah J. Nelson1,3, and Janine M. Lupo1,3

1Surbeck Laboratory of Advanced Imaging, Department of Radiology and Biomedical Imaging, University of California, San Francisco, San Francisco, CA, United States, 2Berkeley Institude of Data Science, Univeristy of Califonia, Berkeley, Berkeley, CA, United States, 3UCSF/UCBerkeley Joint Graduate Group in Bioengineering, San Francisco, CA, United States

Synopsis

This work investigates the feasibility of using arbitrary sampling patterns and GRAPPA-EPSI reconstruction to shorten the acquisition time and increase the spatial resolution of short-echo 3D-MRSI for routine clinical purposes. Fully sampled data were retrospectively under-sampled to achieve effective acceleration rates of 2, 3 and 4 using a variety of sampling patterns. The modified GRAPPA algorithm: 1) took advantage of the FID time points, 2) handled arbitrary sampling patterns, and 3) used a fast, high-resolution external calibration acquisition to estimate sensitivity maps.

Introduction:

Although MR spectroscopic imaging (MRSI) is a powerful tool for diagnosing and monitoring patients with neurological disease, its clinical adaptation remains a challenge due to longer acquisition times, low resolution, and the limited availability of specialized sequences and processing strategies. Although several undersampling and reconstruction strategies for MRSI have been proposed [1-9], the most promising by Sabati et al. that used a spectral-phase-correction (SPC)-GRAPPA reconstruction and enabled voxel sizes as small as 0.31cc with whole-brain coverage, still took 16.4 minutes to acquire [10]. The goal of this study was to design a 5 minute, nearly whole-brain MRSI (24x21x16cm) protocol with 0.56cc resolution using a customized arbitrary-variable-density (AVD)-GRAPPA.

Methods:

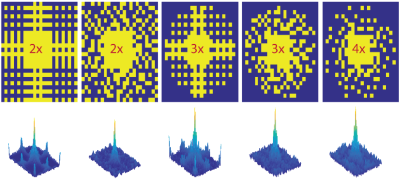
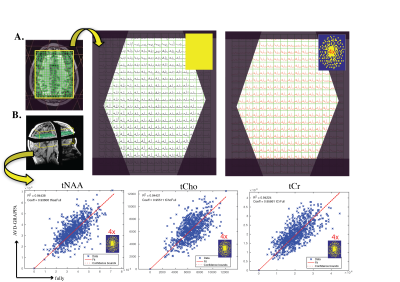
Data Acquisition: Anatomic MRI and MRSI data were acquired in a phantom and 3 volunteers using a 32-channel receive array on a GE 3T scanner. A 1-minute low resolution spin-echo imaging sequence with parameters matching the MRS acquisition (TR/TE=35/1300ms) was acquired for external-calibration of the GRAPPA reconstruction. 3D MRSI was performed with CHESS water suppression, 10 VSS outer volume suppression, spin-echo slice selection, inversion recovery lipid suppression, TE/TR=35/1300ms, a spectral array=28x32x16, a flyback echo-planner trajectory in the SI direction, and spatial resolution of 0.56cc. This fully-sampled MRSI data was acquired in ~20min and used to under-sample by factors of 2, 3, and 4 corresponding to acquisition times of ~10, 7, and 5min using the variable-density sampling patterns shown in Figure1 that were generated from a Poisson-Disc distribution to ensure an equal number of points among subregions.

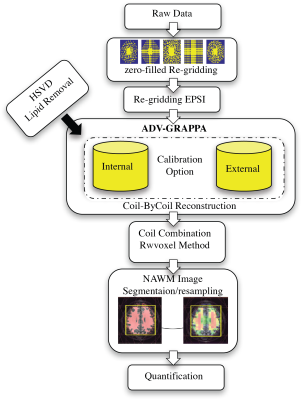
AVD-GRAPPA EPSI: The reconstruction scheme supports optimized arbitrary cartesian sampling patterns, allowing for higher acceleration factors and more-effective control of aliasing artifacts. The hybrid reconstruction bridges the gap between k-space- and image-based PI reconstructions and random sampling by calibrating each k-space point according to its neighborhood to synthesize the missing point, either by obtaining the kernel weights from any number of FID points in the spectral domain or by incorporating a high-resolution external sensitivity calibration. The estimated weights are then applied to all the spectral points (Figure2).

Analysis: The reconstructed spectra were combined, and corrected using in-house software [11,12]. Metabolite levels were quantified with LCModel with simulated basis set from jMRUI [13]. Analysis was limited to a Cramer-Rao lower bounds (CRLB) <10% for tCho, tCr and NAA, and <20% for other metabolites. Voxel-level linear regressions were used to evaluate the accuracy of each reduced k-space sampling and calibration scheme compared to the fully-sampled data.

Results & Discussion:

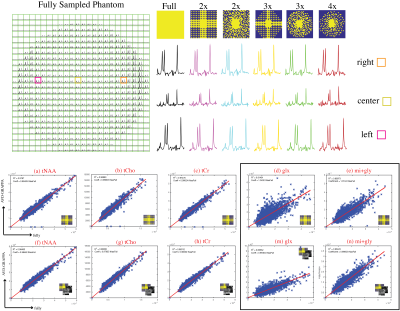
Phantom: Figure3 (Top) shows reconstructed phantom data for fully sampled k-space compared to AVD-GRAPPA reconstruction using Tikhonov regularization to condition the calibration matrix for 5 different sampling patterns using internal-calibration region of sizes 9x9 or 7x7 and a 3x3 kernel-size. The linear regression plots (Figure3:bottom) show a strong correlation between AVD-GRAPPA and the fully-sampled data (R2tNAA=0.98, R2tCho=0.97, R2tCr=0.97, R2glx=0.81, and R2mi+gly=0.90 for internal-calibration and R2tNAA=0.98, R2tCho=0.98, R2tCr=0.98, R2glx=0.87, and R2mi+gly=0.93 for external-calibration). The advantage of incorporating a fully-sampled PD image as the calibration region is observed through a tighter fit for smaller peaks (such as glx or mi+gly) favorable towards external-calibration and in the %mean-difference of metabolites maps decreasing from 6.8% to 2.5%.

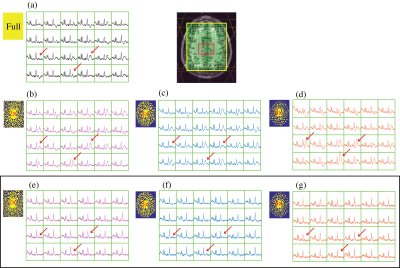
Volunteers: While the PSFs of non-uniform sampling patterns are more complex than simple sinc functions, they provide the added benefit that the aliased lipid signals are incoherent and noise-like, and thus amenable to removal prior to reconstruction. Figure4 shows the benefit of removing Lipid prior to AVD-GRAPPA reconstruction after using random sampling patterns. Using external-calibration improved the traditional ill-conditioning of the PI-MRSI encoding matrix by 6 orders of magnitude, and an additional 60-fold was achieved using Tikhonov regularization. Figure5B shows the metabolites (tNAA, tCho, tCr) for all the voxels within the brain from AVD-GRAPPA data plotted against those obtained from the fully-sampled data using a high-resolution external-calibration matrix for a 4x-acceleration (random). Strong correlations between AVD-GRAPPA and the fully-sampled data were observed (R2tNAA = 0.94, R2tCho = 0.93, R2tCr = 0.93).

Conclusions:

This work demonstrates that whole-brain, short echo 3D-MRSI can be accelerated up to 4-fold at 3T with a 32-channel coil to provide high quality spectra in a clinically feasible scan time of 5min with voxel resolution of 0.56cc in a phantom and volunteers using AVD-GRAPPA. The use of high-resolution external calibration images that were acquired with an extra 1 minute acquisition enhanced the performance by overcoming the limited matrix size of MRSI data that typically poses a challenge for obtaining accurate estimates for reconstruction. Future work will include evaluation of the performance of this technique in whole-brain MRSI data from patients with brain tumors.

Acknowledgements

This work was supported by NIH grants R01 CA127612 and P01 CA118816.

References

[1] Griswold MA, Blaimer M, Breuer F, Heidemann RM, Mueller M, Jakob PM. Parallel magnetic resonance imaging using the GRAPPA operator formalism. Magnetic Resonance in Medicine. 2005;54(6):1553–1556.

[2] Lustig M, Pauly J. SPIRiT: Iterative self‐consistent parallel imaging reconstruction from arbitrary k‐space. Magnetic Resonance in Medicine. 2010.

[3] Dydak, U., et al., Sensitivity-encoded spectroscopic imaging. Magn Reson Med, 2001. 46(4): p. 713-22.


[4] Banerjee, S., et al., Elliptical magnetic resonance spectroscopic imaging with GRAPPA for imaging brain tumors at 3 T. 
Magn Reson Imaging, 2009. 27(10): p. 1319-25.


[5] Ozturk-Isik, E., et al., 3D sensitivity encoded ellipsoidal MR spectroscopic imaging of gliomas at 3T. Magn Reson Imaging, 2009. 27(9): p. 1249-57. 


[6] Hu, S., et al., Compressed sensing for resolution enhancement of hyperpolarized 13C flyback 3D-MRSI. J Magn Reson, 2008. 192(2): p. 258-64.


[7] Hu, S., et al., 3D compressed sensing for highly accelerated hyperpolarized (13)C MRSI with in vivo applications to 
transgenic mouse models of cancer. Magn Reson Med, 2010. 63(2): p. 312-21.


[8] Larson, P.E., et al., Fast dynamic 3D MR spectroscopic imaging with compressed sensing and multiband excitation 
pulses for hyperpolarized 13C studies. Magn Reson Med, 2011. 65(3): p. 610-9.


[9] Hatay, G.H., M. Yildirim, and E. Ozturk-Isik, Considerations in applying compressed sensing to in vivo phosphorus MR 
spectroscopic imaging of human brain at 3T. Med Biol Eng Comput, 2016.


[10] Sabati, M., et al., Impact of reduced k-space acquisition on pathologic detectability for volumetric MR spectroscopic 
imaging. J Magn Reson Imaging, 2014. 39(1): p. 224-34.

[11] Vareth M, Li Y, Lupo JM, Nelson S. Comparison of Several Coil Combination Techniques in Multi-Channel 3D MRSI for Brain Tumor Patients. Proc 23rd Scientific Meeting & Exhibition (ISMRM).

[12] Nelson S. Analysis of volume MRI and MR spectroscopic imaging data for the evaluation of patients with brain tumors. Magnetic Resonance in Medicine. 2001;46(2):228–239.

[13] Pijnappel WWF, van den Boogaart A, DeBeer R, Van Ormondt D. SVD-based quantification of magnetic resonance signals. Journal of Magnetic Resonance. 1992;97(1):122–134.

Figures

Figure 1: Sampling patterns (structured and random) with acceleration factors of 2x ,3x, and 4x with their corresponding Point Spread Functions (PSF) are illustrated. All the sampling patterns are computed with variable density and the random ones are based on a Poisson distribution. For uniform k-space sampling, the PSF is a sinc function, however, the PSF of non-uniform sampling patterns are more complex resulting in different type of errors in the reconstruction.

Figure 2: Data processing flow chart of AVD-GRAPPA reconstruction for 3D-EPSI per slice.

Figure 3: TOP: Reconstructed phantom for fully sampled k-space with individual voxels highlighting the AVD-GRAPPA reconstruction for 5 different sampling patterns using internal-calibration region of sizes 9x9/7x7 with kernel-size of 3x3. BOTTOM: Regression plots of individual metabolites’ concentration (tNAA, tCho, tCr, glx and mi+gly) for structured pattern 2x-acceleration (a,b,c,d,e): AVD-GRAPPA are plotted against their Full k-space using internal-calibration region of size 9x9. (f,g,h,m,n): AVD-GRAPPA are plotted against their Full k-space using high-resolution external-calibration region of PD image.

Figure 4: T1-weighted MRI with in-vivo whole-brain 3D MRSI from a volunteer. The AVD-GRAPPA reconstruction used high-resolution external-calibration with kernel size of [3×3] for 3 random sampling patterns (acceleration 2, 3, and 4x) with and without HSVD as pre-processing step. (a): Full k-space recon (b,c,d): 2, 3, 4x sub-sample recon without lipid removal prior to AVD-GRAPPA. Lipid contamination increases as the acceleration factor increases specially in anterior and posterior regions. (e,f,g) 2, 3, 4x sub-sample recon with HSVD lipid removal prior to AVD-GRAPPA.

Figure 5: (A) Top: T1-weighted MRI with in-vivo 3D Spin-Echo MRSI from a healthy volunteer (TE/TR=35/1300ms, matrix size 28x32x16, flyback in S/I, 4x in-plane acceleration, nominal spatial resolution of 0.56 cc, Tacq = 5min). The AVD-GRAPPA reconstruction was performed using high-resolution external-calibration with kernel size of [3x3]. (B) Bottom: Regression plots of individual metabolites’ concentration (tNAA, tCho, tChr) from all the voxels within the brain. AVD-GRAPPA is plotted against fully sampled k-space.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
3842