3832

Non-linear Mechanics Allows Non-invasive Quantification of Interstitial Fluid Pressure
Daniel Fovargue1, Jack Lee1, Marco Fiorito1, Adela Capilnasiu1, Sweta Sethi2, Stefan Hoelzl1, Jurgen Henk Runge1, Jose de Arcos1, Arnie Purushotham3, Khesthra Satchithananda3, David Nordsletten1, and Ralph Sinkus1

1School of Biomedical Engineering and Imaging Sciences, King's College London, London, United Kingdom, 2Department of Research Oncology, Guy's and St Thomas' NHS Foundation Trust, London, United Kingdom, 3Division of Cancer Studies, King's College London, London, United Kingdom

Synopsis

Established tumour treatments include drugs and the emerging class of cell-based therapies. Individual tumours can counteract the delivery of the therapy, for example, they can feature high internal pressures (IFP) caused by blood vessels that are different from normal tissues. Furthermore, a drop in IFP is a well-established marker for successful therapy. Here we demonstrate in simulations, phantom experiments, fatty breast tissue, and a benign breast lesion that tissue biomechanics as quantified via MR-Elastography (MRE) allows in combination with non-linear mechanics to estimate IFP in absolute units non-invasively.

Introduction

Current tumour treatments include drugs as well as the emerging class of cell-based therapies. Treatment success depends on whether these therapeutics can reach the tumours, for which the blood vessels are the essential roads. Individual tumours can counteract the delivery of the therapeutic, for example, they can feature high interstitial fluid pressures (IFP) caused by blood vessels that are abnormal (e.g. leaky, misconnected etc.). Furthermore, a drop in IFP is a well-established marker for successful therapy. However, a major current unmet clinical need is to quantify IFP non-invasively in order to stratify patients before and during therapy. Here we demonstrate in simulations, phantom experiments, fatty breast tissue, and a benign breast lesion that tissue biomechanics as quantified via MR-Elastography (MRE) allows in combination with non-linear mechanics to estimate IFP in absolute units non-invasively.

Methods

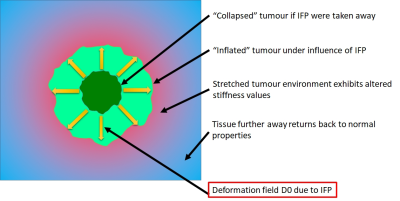
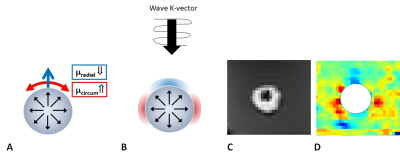
Elevated IFP within the lesion will inflate the tumour and impose a force onto its surrounding (Fig.1). Consequently, the tumour environment is stretched by the deformation field D0. Since tissue exhibits non-linear material properties, the apparent shear modulus will depend upon the local deformation tensor. Radial shear modulus will decrease due to a compression, while circumferential shear modulus will increase due to stretch (Fig.2A). A shear wave that travels through this tumour environment will, depending on its propagation vector K, sense regionally altered apparent moduli (Fig.2B). The leading side of the inflated object will exhibit reduced values, while in the lateral area, increased values compared to the background stiffness. This has been demonstrated previously1 and new improved results for an inflated balloon inserted within a polymer phantom are shown in Fig.2C,D confirming this “butterfly pattern”. Thus, MRE is capable of quantifying this modified mechanical environment in the vicinity of the inflated object.

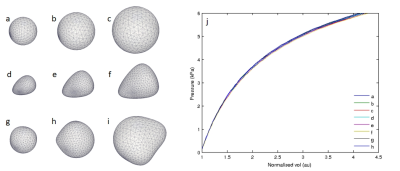
Our concept of estimating IFP is based upon the idea to virtually deflate the tumour. Mathematically this is analogous to reversing the deformation field D0 in order to recover the state of modulus distribution prior to the stretching effect of IFP. The MRE experiment provides the shear wave field in the inflated state which is under the influence of the non-linear material response. Using these wave fields, we solve the classical linear wave equation whose spatial operators have been scaled according to deformation gradients corresponding to a hypothetical deformation D0*. We consider an idealized radial symmetric deformation mode which is scaled by the “contraction” parameter alpha. The optimal value for alpha is found when the minimum of the objective function (i.e. the variance of the elasticity distribution) is obtained. A value of alpha=0 means that the object has not undergone inflation, while alpha=1 means that the object will collapse to a point if IFP were taken away. Fig.3 shows different initial shapes and sizes of objects subject to a simulated inflation. As clearly visible, the finer shape variations are unimportant when considering the pressure volume relationship.

The validity of this approach is demonstrated via simulation, a polymer phantom with known pressure of the inflated balloon, and the first in-vivo results in fatty breast tissue as well as in a fibroadenoma are presented.

Results

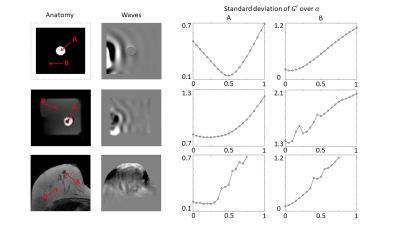
Fig.4, 1st row shows the simulation results in which a spherical pore is inflated within a block of non-linearly elastic material. The wave equation on top of the deformed material is then solved to provide virtual MRE data of the propagating waves. Since the inflation caused the pore size to double, we expect the minimum of the objective function to be at alpha=0.5, as shown in the 3rd column (A). Also, as expected, a point located further away from the inflated pore (4th column, B) is not influenced by the pressure and therefore the analysis yields a minimum of the objective function at alpha=0. The 2nd row shows the polymer phantom experiments where the balloon was inflated with a pressure of 6kPa. The corresponding objective function yields a minimum at alpha=0.25 (3rd column, A) which leads to a pressure estimate of 4.5kPa. Again as expected, a reference point further away from the balloon (4th column, B) yields a minimum at alpha=0. Finally, first in-vivo results are shown in the 3rd row. The fibroadenoma (A) exhibits a minimum of the objective function at alpha=0.2 which corresponds to 0.3kPa, as expected for such a lesion2. A reference point in the fatty tissue (4th column, B) yields as expected a minimum at alpha=0.

Discussion

We demonstrate that MRE in combination with non-linear mechanics is capable to quantify IFP non-invasively. More experiments are currently underway to further validate this approach.

Acknowledgements

This project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 668039.

References

1. Using non-linear tissue biomechanics to infer static forces within tissue: towards quantifying IFP, ISMRM 2017, #0973

2. Interstitial fluid pressure in breast cancer, benign breast conditions, and breast parenchyma. Annals of Surgical Oncology, 1(4):333-338 (1994)

Figures

Figure 1. General concept of modified mechanical environment surrounding an inflated tumour. Our concept is to find the deformation field D0 that occurs when the tumour is exposed to IFP. In the absence of IFP, it would collapse to its base state.

Figure 2. Evolution of apparent stiffness in the vicinity of an inflated object probed by a shear wave that propagates in the direction indicated by the K-vector (A,B). C: inflated balloon within a non-linear polymer phantom material and corresponding apparent elasticity map that shows the expected butterfly pattern (D).

Figure 3. For simulated tumours of various sizes and shapes (a to i), the pressure – volume (normalised to the initial volume) curves yield a highly consistent relationship (j), allowing the inflating pressure to be identified, once alpha is found. (Shown relationship is for surrounding tissue of fixed shear modulus).

Figure 4. Row 1: simulation results, row 2: phantom experiments, row 3: in-vivo breast tissue. Column 1: magnitude image of the object, column 2, example of a shear wave component, column 3, objective function as a function of contraction parameter alpha at the inflated object, column 4, objective function as a function of contraction parameter alpha at a reference point.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
3832