3819
In Vivo Assessment of Lauren Classification for Gastric Cancer Using Diffusion MRI with a Fractional Order Calculus ModelMuge Karaman1, Lei Tang2, Ziyu Li3, Yu Sun4, Jia Fu Ji3, and Xiaohong Joe Zhou1,5
1Center for Magnetic Resonance Research, University of Illinois at Chicago, Chicago, IL, United States, 2Department of Radiology, Peking University Cancer Hospital and Institute, Beijing, China, 3Department of Gastrointestinal Surgery, Peking University Cancer Hospital and Institute, Beijing, China, 4Department of Pathology, Peking University Cancer Hospital and Institute, Beijing, China, 5Departments of Radiology, Neurosurgery, and Bioengineering, University of Illinois at Chicago, Chicago, IL, United States
Synopsis
Gastric cancer (GC) is the second most common cause of cancer-related mortality globally. Histological assessment of GC has been based on Lauren classification which categorizes the tumor according to its morphological features. In respond to the need for probing biological tissue complexity, a growing number of diffusion-weighted imaging studies have focused on revealing tissue microstructures by measuring non-Gaussian diffusion behaviors. One of these techniques is the fractional order calculus (FROC) model. In this study, we have used the FROC model to investigate non-invasive imaging-based assessment of GC, providing an alternative to histopathology-based Lauren classification.
Introduction
As the second leading cause of cancer-associated mortality1, gastric cancer (GC) is one of the most common types of cancer worldwide. Lauren classification is commonly employed to divide GC into intestinal type (IT), diffuse type (DT), and mixed type (MT; combination of IT and DT), each with distinct molecular and clinical characteristics2. The sensitivity of GC to different treatment strategies, such as neoadjuvant chemotherapy and pre-/post-operative chemoradiotherapy, varies according to Lauren classification3,4. Thus, Lauren classification is important for tailoring individualized therapy as well as following treatment response. Lauren classification involves invasive biopsy procedures that are susceptible to sampling errors. With its sensitivity to tissue structures in vivo, diffusion-weighted imaging (DWI) may provide information similar to Lauren classification noninvasively while avoiding sampling errors. In this study, we employ a non-Gaussian DWI technique with a fractional order calculus (FROC) model5-10 to investigate the possible correlations between the FROC model parameters and Lauren classification in a group of GC patients.Methods
Patients: The study enrolled 28 patients with confirmed GC who underwent chemotherapy followed by gastrectomy. Surgical specimens were obtained for histopathological analysis to determine Lauren classification, resulting in 7 patients with DT, 12 with IT, and 9 with MT. For the analysis, the DT and MT were combined as mixed-and-diffuse type (MDT) and compared with the IT. Image Acquisition: All patients were scanned on a 1.5T Siemens Aera scanner. The MRI protocol included T1-weighted (VIBE), T2-weighted (turbo spin echo with respiratory-trigger), and DWI with 11 b-values (0 to 2000 s/mm2) with the following parameters: TR/TE=4400/62ms, slice thickness=5mm, FOV=28.5cm×38cm, and reconstruction matrix=128×96. Trace-weighted images were obtained to minimize the effect of diffusion anisotropy. DWI Analysis: The multi-b-value diffusion images were analyzed with the FROC model5-7,$$S/S_0=\exp\left[-D\mu^{2(\beta-1)}\left(\gamma G_d\delta\right)^{2\beta}\left(Δ-\frac{2\beta-1}{2\beta+1}\right)\delta\right], (1) $$ which yields a set of diffusion parameters: an anomalous diffusion coefficient D (in μm2/ms), a spatial parameter μ (in μm), and a spatial fractional order measure β (dimensionless) that has been linked to intra-voxel tissue heterogeneity8-10. In Eq. (1), Gd is gradient amplitude, δ (51ms) is pulse width, and Δ (100.6ms) is lobe separation. A least squares algorithm was used for nonlinear fitting to obtain the three model parameters. For comparison, a conventional mono-exponential model was also used to compute ADC by using images from two b-values of 50 and 800 s/mm2. Statistical Analysis: For each patient, the regions-of-interest (ROIs) were drawn on b=0 images guided by other anatomic images. For group analysis, the test parameters for each individual patient were computed as the mean value from the selected ROI for β and μ, and from the lower 10% of the D or ADC histogram to improve robustness against contamination from the body fluid whose water diffusion is drastically faster. A Mann-Whitney U test was used for the group comparison, followed by a receiver operating characteristic (ROC) analysis to assess the performance of the FROC model with its multiple parameters for GC classification in comparison with ADC.Results
Figure 1a shows ADC, D, β, and μ maps from a representative patient in each of the DT, MT, and IT groups. The DT and MT lesions showed lower mean ADC, D, and β, and higher μ than the IT lesions (Fig. 1b). The differences in the diffusion parameters were substantiated in the group analysis, as illustrated by the box-and-whisker plots (Fig. 2a) and descriptive statistics (Fig. 2b) where statistical significance (p-values<0.05) was achieved. Figure 3 summarizes the ROC results of using different combinations of the FROC parameters as well as ADC for imaging-based classification of MDT and IT. The (D, β, μ) combination showed the best overall performance, yielding the highest accuracy (0.862) and area-under-the-curve (AUC, 0.911) while providing a high sensitivity (0.882) and specificity (0.833). Overall, the FROC parameters outperformed ADC.Discussion and Conclusion
Our results showed that the FROC model, which offers additional parameters that are sensitive to tissue microstructures (β and μ), performed better than ADC for imaging-based assessment of Lauren classification in GC. Using an automated “filter” based on the lower 10% of diffusion parameters within an ROI, our approach not only provides robustness against contamination from body fluid, but also is consistent with the histopathology practice where worse-case scenario in typically used to make a diagnosis11. The novel approach and encouraging results may lead to a non-invasive imaging-based method for obtaining the similar information to Lauren classification for characterizing GC. With further validation, the non-invasive approach described herein is expected to enable repeated evaluations of GC at various time points throughout the disease progression and regression.Acknowledgements
This work was supported in part by NIH 1S10RR028898 and grants from National Natural Science Foundation of China No. 81171308 and No. 81401389. MK and LT contributed equally to this work.References
- Jemal A, Bray F, Center MM, et al. Global cancer statistics. CA Cancer J Clin. 2011;61:6990.
- Lauren P. The two histological main types of gastric carcinoma: Diffuse and so-called intestinal-type carcinoma. An attempt at a histo-clinical classification. Acta Pathol Microbiol Scand. 1965;64:3149.
- Ma J, Shen H, Kapesa L, et al. Lauren classification and individualized chemotherapy in gastric cancer. Oncology Letters. 2016;11(5):2959-2964.
- Jackson C, Mochlinski K, Cunningham D. Therapeutic options in gastric cancer: neoadjuvant chemotherapy vs postoperative chemoradiotherapy. Oncology (Williston Park) 2007;21:1084–1087.
- Magin RL, Abdullah O, Baleanu D, et al. Anomalous diffusion expressed through fractional order differential operators in the Bloch-Torrey equation. J Magn Reson Im. 2008;190:255–270.
- Zhou XJ, Gao Q, Abdullah O, Magin RL. Studies of anomalous diffusion in the human brain using fractional order calculus. Magn Reson Med. 2010;63:562–569.
- Ingo C, Magin RL, Colon-Perez L, et al. On random walks and entropy in diffusion-weighted magnetic resonance imaging studies of neural tissue. Magn Reson Med. 2014;71(2):617–27.
- Sui Y, He W, Damen FW, et al. Differentiation of low- and high- grade pediatric brain tumors with high b-value diffusion weighted MR imaging and a fractional order calculus model. Radiology. 2015;277(2):489–496.
- Tang L, Sui Y, Zhong Z, et al. Non-Gaussian diffusion imaging with a fractional order calculus model to predict response of gastrointestinal stromal tumor to second-line sunitinib therapy. Magn Reson Med. 2017.
- Sui Y, Xiong Y, Xie KL, et al. Differentiation of low- and high-grade gliomas using high b-value diffusion imaging with a non-Gaussian diffusion model. Am J Neuroradiol. 2016; 37(9):1643-1649.
- Just N. Improving tumour heterogeneity MRI assessment with histograms. British Journal of Cancer. 2014;111(12):2205-2213.
Figures
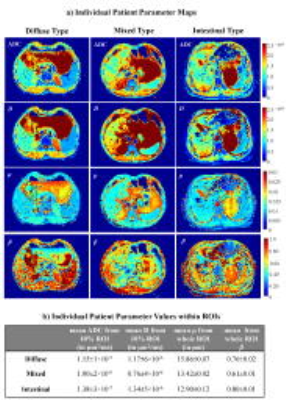
Figure 1: a) Maps of ADC, D, μ, and β from a representative patient in each of the DT (first column), MT (middle column), and IT (last column) GC groups. The ROIs are shown with black contours in the parameter maps. b) The descriptive statistics, showing sample mean and standard deviation, ($$$\bar{x}$$$±σ), of the test parameter values for DT, MT, and IT GCs.

Figure 2: a) Box-and-whisker plots of D, β, μ, and ADC. b) The corresponding descriptive
statistics, showing sample mean and standard deviation, ($$$\bar{x}$$$±σ), of the test parameter values for
MDT and IT GC groups (first two rows). The p-values
for the statistical significance of the difference between the test parameter
values are indicated in the last row.
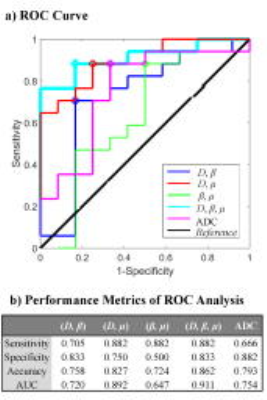
Figure 3: a) The ROC curves of using the different combinations of D, β, and μ for classifying GCs as MDT and IT. b) Summary of the corresponding best cut-off sensitivity and specificity values (shown as circles in the curves) as well as the accuracy and the AUC for the ROC curves. The different combinations of the parameters were obtained by using a multivariate logistic regression algorithm.