3568
Extended Signal Modelling and Regularization for Multi-Echo Hyperpolarized Metabolic Image Reconstruction1Institute for Biomedical Engineering, University of Zurich and ETH Zurich, Zurich, Switzerland, 2Division of Surgical Research, University Hospital Zurich, Zurich, Switzerland
Synopsis
The IDEAL signal model for hyperpolarized metabolic imaging is extended and spatiotemporal regularization and b0-map recalibration is included. The approach is tested on simulated data and in-vivo metabolic imaging data of the heart. Allowing variable b0-fields and including sparsity regularization signal leakage and ghosting can be significantly reduced (average reduction of root-mean-square error (RMSE) by 16% and 30%). Spatial and temporal regularization of the metabolite intensities considerably improved accuracy of the estimate in terms of RMSE with additional reductions by 68% and 20%, respectively. Thus, the metabolic conversion of [1-13C]pyruvate into [1-13C]lactate and 13C-bicarbonate can be measured with improved accuracy.
Introduction
Dynamic nuclear polarization1,2 enables the assessment of metabolic conversion of 13C substances in-vivo3-6. Multi-echo acquisition schemes in combination with IDEAL reconstruction7,8 have been used for 13C metabolic imaging9,10. Since the IDEAL reconstruction is phase-sensitive, accurate knowledge of the b0 induced phase offsets is of particular importance and more advanced reconstruction techniques have to be applied11. In the present work, the IDEAL signal model is extended and an iterative estimation of the b0 induced phase offsets is included. The approach is tested on simulated data and in-vivo metabolic imaging data of the heart.Theory
If a multi-echo acquisition is combined with an echo-planar imaging readout, the IDEAL signal model8,12 has to account for the chemical shift dependent spatial shift each metabolite undergoes:
$$${u}_{n}\left(\mathbf{k}\right)=\underbrace{\underset{m=1}{\overset{M}{\mathop\sum }}\,{{e}^{i2\pi \Delta{\nu}_{m}{t}_{n}}}{{e}^{-i\mathbf{k}\Delta{\mathbf{r}}_{m}}}\underset{r}{\mathop\sum }\,{{e}^{i\mathbf{kr}}}}_{\mathbf{E}'}\underbrace{{{w}_{m,n}}\left(\mathbf{r}\right)}_{\mathbf{W}\left(\mathbf{w}\right)}\underbrace{{{e}^{i2\pi\tilde{\gamma}{{b}_{0}}\left(\mathbf{r}\right){{t}_{n}}}}}_{\mathbf{W}\left(\mathbf{{b}_{0}}\right)}{{\mathbf{\rho}}_{m}}\left(\mathbf{r}\right)$$$, [1]
with $$$\mathbf{\rho}_m\left(\mathbf{r}\right)$$$: intensities of
the M metabolites at location $$$\mathbf{r}$$$; $$$\Delta\nu_{m}$$$: chemical shift;
$$$u_{n}\left(\mathbf{k}\right)$$$: k-space signal
of the n-th echo; $$$t_{n}=TE+\Delta t_{n}$$$: echo time; $$$b_{0}\left(\mathbf{r}\right)$$$: b0-phase
offsets in Hz; $$$\tilde{\gamma
}=\frac{{{\gamma }_{13C}}}{{{\gamma }_{1H}}}$$$: the scaling ratio between the gyromagnetic ratio of
13C and 1H; $$$\Delta\mathbf{r}_{m}=\Delta\mathbf{r}\left(\Delta\nu_{m}\right)$$$: spatial shift. To
address scaling of the signal magnitude $$$\rho_{m}$$$ between different echoes due to T2*-
dephasing, flip angle dependent signal saturation or inflow effects, a
weighting function $$$w_{m,n}$$$ with $$$\rho_{m,n}=w_{m,n}\rho_{m}$$$ is introduced.
Equation [1] can be written in
matrix notation and formulated as an optimization problem
$$$\arg~\underset{\mathbf{\rho}}{\mathop{\min}}\,\left\| \mathbf{{E}'W}\left(\mathbf{w}\right)\mathbf{W}\left(\mathbf{{b}_{0}}\right)\mathbf{\rho} -\mathbf{u} \right\|_{2}^{2}$$$, [2]
where $$$\left\|\text{ }\right\|_{2}^{2}$$$ denotes the L2-norm. To account for low SNR of in vivo acquisition combined with inaccuracies in b0-phase maps and flip angle values, the model is extended using spatiotemporal regularization and b0-map recalibration. The regularized model fit quality is defined as
$$$\mathcal{F}\left(\mathbf{\rho},~{\mathbf{b}_{0}}|\mathbf{w},~\mathbf{u} \right)={{\lambda}_{\text{n}}}\left\|\mathbf{{E}'W}\left(\mathbf{w}\right)\mathbf{W}\left({\mathbf{b}_{0}}\right)\mathbf{\rho}-\mathbf{u}\right\|_{2}^{2}+{{\lambda}_{s}}{{\left\|\mathbf{\rho}\right\|}_{1}}+{{\lambda}_{\text{TV}}}\text{TV}\left(\mathbf{\rho}\right)+{{\lambda}_{t}}{{\left\|{{\mathbf{D}}_{2}}\mathbf{\rho}\right\|}_{1}}+{{\lambda}_{{{b}_{0}}}}\text{TV}\left({\mathbf{b}_{0}}\right)$$$. [3]
Here, TV denotes isotropic total variation and $$${{\mathbf{D}}_{2}}$$$ the second order derivative in temporal direction. The cost function [3] is iteratively minimized with the optimization algorithm ADAM13.
Methods
The algorithm to minimize cost function [3] was
implemented in Python using the Tensorflow 1.314 framework
and executed on GPU (NVIDIA Titan Xp) with IEEE 754 32-bit floating-point
format.
Based on the MRXCAT phantom data15 and realistic intensity time curves the metabolic conversion of pyruvate
into lactate, alanine and bicarbonate was simulated according to equation [1]. Healthy
female pigs (N=6, 30-35kg) were anesthetized using propofol or isoflurane and
ventilated with oxygen. Venous catheters for medication and injection of
hyperpolarized substances were introduced. Animals were placed in a 3T Philips
Ingenia system (Philips Healthcare, Best, The Netherlands) equipped with a
custom-built four-channel 13C transmit/receive coil (Clinical MR
Solutions, Brookfield WI, USA). A glucose (20%) - insulin (50U/L) solution16-18 was infused with a loading rate of 3ml/kg/h
for 60 minute and a maintenance rate (1-3ml/kg/h) thereafter. All experiments
were performed in accordance with the Swiss Animal Protection Law and
Ordinance. 0.5ml of [1-13C]pyruvic acid was prepared in a commercial SpinLab
Hyperpolarizer (GE Healthcare, Waukesha, WI, USA). Upon dissolution, 20ml of the
225mM pyruvate solution was injected into the femoral vein.
Immediately following injection, three slices were dynamically acquired using a
multiband multi-echo excitation acquisition scheme10 (resolution: 5x5x20mm3, field-of-view: 220x220mm2,
75% partial Fourier, echo time/repetition time: 12ms/32ms, no. echoes: 7, echo spacing: 1.1ms). For
excitation, a 1-2-1 binomial excitation pulse of 20ppm bandwidth and 30⁰ flip
angle was used.
An additional 1H b0-map was
acquired using the 2-channel body coil of the scanner. Sequence parameters were: 3 slices, resolution: 2.5x2.5x8mm3, field-of-view: 321x251x48mm3, echo time/repetition time: 1.3ms/3.9ms and flip angle 20°. All regularization
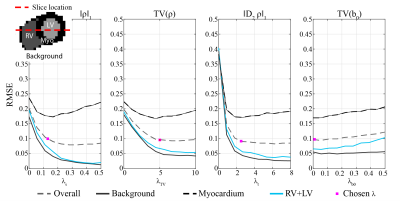
weights $$$\lambda=\{\lambda_{S},\lambda_{TV},\lambda_{t},\lambda_{b_0}\}$$$ were tuned
on synthetic data by minimizing the mean root mean square error (RMSE) relative to ground truth over the myocardium, left ventricle (LV), right
ventricle (RV) and background (Figure 1), yielding $$$\lambda^\star=\{0.13,5.0,2.5,0.01\}$$$. Results
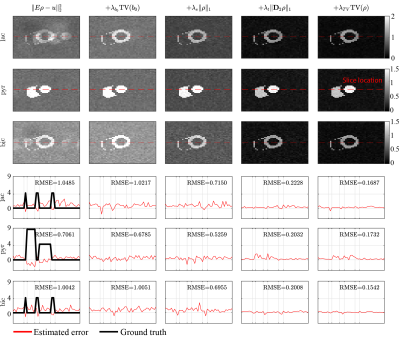
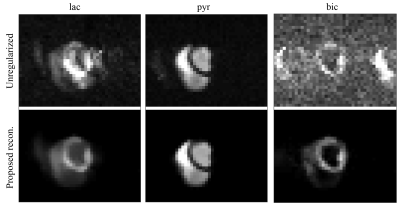
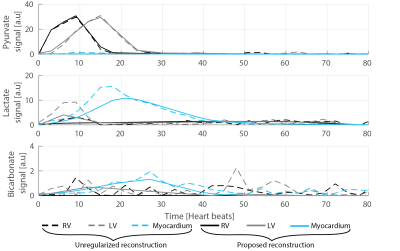
Without regularization the time-averaged lactate and bicarbonate images show ghosting and signal leakage which can be reduced using isotropic TV regularization on b0 (average reduction of RMSE by 16%). The consecutive introduction of sparsity, temporal and spatial regularization result in further reduction of the RMSE by 30%, 68% and 20%, respectively, with an overall improvement by 85% in RMSE when compared to the unregularized reconstruction (Figure 2). In-vivo, ghosting and signal leakage artifacts are greatly reduced (Figure 3). In particular, lactate and bicarbonate images show reduced artifacts in the myocardium. Temporal signal intensity time curves averaged over cardiac compartments show good separation of the metabolite signals (Figure 4).Discussion
Allowing variable b0 fields and including sparsity regularization, signal leakage and ghosting can be significantly reduced. Spatial and temporal regularization of the metabolite intensities considerably improved accuracy of the estimate in terms of RMSE. With the presented sequence and reconstruction algorithm the metabolic conversion of [1-13C]pyruvate into [1-13C]lactate and 13C-bicarbonate can be measured with improved accuracy.Acknowledgements
No acknowledgement found.References
1. Ardenkjaer-Larsen JH, Fridlund B, Gram A, et al.: Increase in signal-to-noise ratio of > 10,000 times in liquid-state NMR. Proc Natl Acad Sci U S A 2003; 100:10158–63.
2. Ardenkjaer-Larsen JH, Leach AM, Clarke N, Urbahn J, Anderson D, Skloss TW: Dynamic nuclear polarization polarizer for sterile use intent. NMR Biomed 2011; 24:927–32.
3. Golman K, in ’t Zandt R, Thaning M: Real-time metabolic imaging. Proc Natl Acad Sci U S A 2006; 103:11270–5.
4. Golman K, Petersson JS, Magnusson P, et al.: Cardiac metabolism measured noninvasively by hyperpolarized 13C MRI. Magn Reson Med 2008; 59:1005–13.
5. Nelson SJ, Kurhanewicz J, Vigneron DB, et al.: Metabolic Imaging of Patients with Prostate Cancer Using Hyperpolarized [ 1- 13 C ] Pyruvate. Sci Transl Med 2013; 5:198ra108.
6. Cunningham CH, Lau JYC, Chen AP, et al.: Hyperpolarized 13 C Metabolic MRI of the Human Heart. Circ Res 2016; 119:1177–1183.
7. Glover GH: Multipoint Dixon technique for water and fat proton and susceptibility imaging. J Magn Reson Imaging 1991; 1:521–30.
8. Reeder SB, Wen Z, Yu H, et al.: Multicoil Dixon chemical species separation with an iterative least-squares estimation method. Magn Reson Med 2004; 51:35–45.
9. Wiesinger F, Weidl E, Menzel MI, et al.: IDEAL spiral CSI for dynamic metabolic MR imaging of hyperpolarized [1- 13C]pyruvate. Magn Reson Med 2012; 68:8–16.
10. Sigfridsson A, Weiss K, Wissmann L, et al.: Hybrid multiband excitation multiecho acquisition for hyperpolarized (13) C spectroscopic imaging. Magn Reson Med 2015; 73:1713–7.
11. Wiens CN, Friesen-Waldner LJ, Wade TP, Sinclair KJ, McKenzie CA: Chemical shift encoded imaging of hyperpolarized 13C pyruvate. Magn Reson Med 2015; 74:1682–1689.
12. Reeder SB, Pineda AR, Wen Z, et al.: Iterative decomposition of water and fat with echo asymmetry and least-squares estimation (IDEAL): application with fast spin-echo imaging. Magn Reson Med 2005; 54:636–44.
13. Kingma DP, Ba JL: Adam: A method for stochastic optimization. In Proc ICLR; 2013:1–15.
14. Abadi M, Agarwal A, Barham P, et al.: TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. Softw available from tensorflow.org 2015.
15. Wissmann L, Santelli C, Segars WP, Kozerke S: MRXCAT : Realistic numerical phantoms for cardiovascular magnetic resonance. J Cardiovasc Magn Reson 2014; 16:1–11.
16. Schroeder MA, Cochlin LE, Heather LC, Clarke K, Radda GK, Tyler DJ: In vivo assessment of pyruvate dehydrogenase flux in the heart using hyperpolarized carbon-13 magnetic resonance. Proc Natl Acad Sci U S A 2008; 105:12051–6.
17. Lauritzen MH, Laustsen C, Butt SA, et al.: Enhancing the [(13) C]bicarbonate signal in cardiac hyperpolarized [1-(13) C]pyruvate MRS studies by infusion of glucose, insulin and potassium. NMR Biomed 2013; 26:1496–500.
18. Søvsø Szocska Hansen E, Stilling Tougaard R, Stokholm Nørlinger T, et al.: Imaging porcine cardiac substrate selection modulations by glucose , insulin and potassium intervention : A hyperpolarized [ 1 ‐ 13 C ] pyruvate study. NMR Biomed 2017; 30:1–7.
Figures