Synopsis

We show preliminary results of hyperpolarized [1-¹³C]pyruvate injected in 9 patients affected with glioma.

Raw data showed excellent SNR. Variable bolus delivery and magnitude images introduced errors in modeling the conversion of pyruvate into lactate: kinetic models were presented and compared quantitatively to address these issues.

Finally, reliable and spatially-resolved maps of k_PL rates were obtained, which can be useful in future to assess the clinical relevance of the method for both diagnosis and response to therapy.

Introduction

Dissolution Dynamic Nuclear Polarization (dDNP)^[1] is a powerful technique enhancing nuclear polarization by up to 5 orders of magnitude and its clinical potential is being investigated.

Pyruvate is intensively studied for dDNP in-vivo applications because of its long T₁(¹³C) and high biological relevance: it has already provided valuable information in both pre-clinical^[2] and recent clinical^[3] studies. We present preliminary clinical research results of the injection of hyperpolarized [1-¹³C]pyruvate in 9 patients affected with glioma.

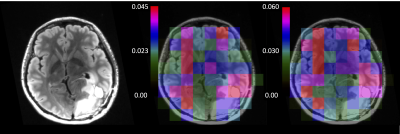
The goal of this work was to develop, implement and test methods for calculating reliable k_PL maps describing the label exchange from [1-¹³C]pyruvate to [1-¹³C]lactate, to be used in larger-scale studies to investigate its clinical value for diagnosis and follow-up.

Methods

A GE SpinLab^[4] polarizer was used to enhance the polarization of [1-¹³C]pyruvate up to about 40% in the solid state at cryogenic temperatures.

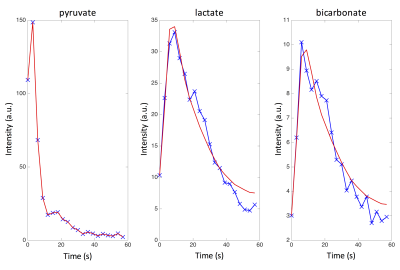
Experiments were carried on a 3T MRI scanner equipped with either a 8 or 32 channels ¹³C RF coil for detection. The acquisition scheme consisted of an EPI dynamic sequence^[5] with: 8 slices, 2 cm thick axial slice, TR=0.13 s, TE=6.1 ms, 20 time points, 3 s time resolution, variable in-plane resolution of 1.2x1.2 cm² or 2x2 cm². Temporal magnitude images of pyruvate, lactate and bicarbonate were acquired (figure 1). Excellent peak SNR of 600 and 100 was achieved for pyruvate and lactate; the SNR of bicarbonate varied among data sets. See figure 2 for examples in a voxel.

Overall, 15 data sets were acquired on 9 glioma patients.

Kinetic models

Consider the general model $$$\frac{\text{d}}{\text{d}t}\widehat{M}(t)=\widehat{\widehat{K}}\cdot\widehat{M}(t)+\widehat{Γ}(t)$$$, where:

$$$\widehat{\widehat{K}}=\begin{bmatrix}-R_{1}-k_{PL}-k_{PB} & k_{LP} & k_{BP} \\k_{PL} & -R_{1}-k_{LP} & 0 \\k_{PB} & 0 & -R_{1}-k_{BP} \end{bmatrix}$$$

$$$\widehat{M}(t)=\begin{bmatrix}M^{pyr}(t) \\M^{lac}(t) \\M^{bic}(t) \end{bmatrix}$$$, $$$\widehat{Γ}(t)=\begin{bmatrix}Γ(t) \\Γ(t) \cdot c_{lac}\\Γ(t) \cdot c_{bic} \end{bmatrix}$$$ and $$$Γ(t)=\alpha\cdot e^{\beta t} \cdot t^{\gamma}$$$

We tested 6 different approaches:

A) $$$Γ(t)=0$$$, $$$k_{LP}=k_{BP}=0$$$, $$$M^{pyr}(t)=M^{pyr}_{EXP}(t)$$$, $$$\widehat{M}(0)=\widehat{M}_{EXP}(0)$$$, $$$\widehat{M}(\infty)=\widehat{M}_{EXP}(\infty)$$$. Fitted parameters: $$$k_{PL}$$$, $$$k_{PB}$$$, $$$R_{1}$$$.

B) Same as A) except for having now $$$k_{LP}=k_{PL}\neq0$$$ and $$$k_{BP}=k_{PB}\neq0$$$. Fitted parameters: $$$k_{PL}$$$, $$$k_{PB}$$$, $$$R_{1}$$$.

C) Same as A) except for having now $$$k_{LP}\neq0$$$ and $$$k_{BP}\neq0$$$. Fitted parameters: $$$k_{PL}$$$, $$$k_{PB}$$$, $$$k_{LP}$$$, $$$k_{BP}$$$, $$$R_{1}$$$.

D) Same as A) except for having now $$$\widehat{M}^{T}(\infty)=\begin{bmatrix}{M}^{fit}_{\infty} & {M}^{fit}_{\infty} &{M}^{fit}_{\infty} \end{bmatrix}$$$. Fitted parameters: $$$k_{PL}$$$, $$$k_{PB}$$$, $$$R_{1}$$$, $$${M}^{fit}_{\infty} $$$.

E) Same as A) except for having now $$$\widehat{M}^{T}(\infty)=\begin{bmatrix}{M}^{fit}_{\infty} & {M}^{fit}_{\infty} &{M}^{fit}_{\infty} \end{bmatrix}$$$ and $$$\widehat{M}^{T}(0)=\begin{bmatrix}{M}^{fit}_{0} & {M}^{fit}_{0} &{M}^{fit}_{0} \end{bmatrix}$$$.

Fitted parameters: $$$k_{PL}$$$, $$$k_{PB}$$$, $$$R_{1}$$$, $$${M}^{fit}_{\infty} $$$, $$${M}^{fit}_{0} $$$.

F) $$$k_{LP}=k_{BP}=0$$$, $$$\widehat{M}(0)=\widehat{M}_{EXP}(0)$$$, $$$\widehat{M}(\infty)=\widehat{M}_{EXP}(\infty)$$$. Fitted parameters: $$$k_{PL}$$$, $$$k_{PB}$$$, $$$R_{1}$$$, $$$\alpha$$$, $$$\beta$$$, $$$\gamma$$$, $$$c_{lac}$$$, $$$c_{bic}$$$.

Custom MATLAB routines were used to fit data to the models.

Results and discussion

Modeling suffered from errors induced by variable bolus delivery ($$$\pm3$$$ s) and magnitude images (non-zero mean noise) and discarding voxels with poor fitting was found to be critical to provide reliable k_PL maps.

In this section, we describe and compare kinetic models and fitting criteria to address these issues.

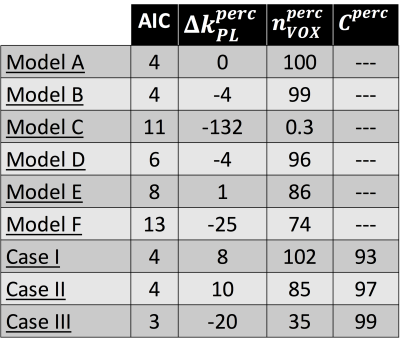
First, we adopted the "error criterion": initially all voxels were allowed to be fitted, then we discarded those with an error on the fitted k_PL bigger than the k_PL itself. Models A-F in Section 3 were compared (figure 3 and table 1) according to 3 indicators: Akaike Information Criterion (AIC) and percentage deviations from model A of mean k_PL (i.e.,$$$\triangle k_{PL}^{perc}= 100\cdot\left[1-\left(k_{PL}^{i}/k_{PL}^{A}\right)\mid_{mean}\right]$$$ with i=A,B,C,D,E,F) and of n_VOX (i.e., $$$n_{VOX}^{perc}=n_{VOX}^{i}/n_{VOX}^{A}\cdot100$$$). Model A is the best at describing data (highest n_VOX and lowest AIC) and model C the worst (high AIC and negligible n_VOX).

Then, we compared the "error criterion" with the "SNR criterion" in which voxels with peak SNR lower than a threshold are discarded in k_PL maps. We tested model A with 3 sets of SNR thresholds for pyruvate and lactate (figure 4): 5 and 2 (case I), 10 and 2 (case II), 5 and 5 (case III). C^perc is the percentage of voxels fitted according to the "SNR criterion" which fulfill also the "error criterion". Moving from case I to III in table 1, AIC and $$$n_{VOX}^{perc}$$$ decrease and C^perc increases: in the "SNR criterion" the number of reliable voxels dropped down by a -65% to achieve higher statistical significance.

Finally, bias introduced by magnitude images were estimated with model A and power images^[6]: $$$\triangle k_{PL}^{perc}$$$=62% suggests that ignoring bias likely leads to underestimating k_PLs.

Model A, "error criterion" and power images are optima from the discussed perspectives.

Conclusions

Preliminary studies of hyperpolarized pyruvate injected in patients affected with glioma demonstrated the feasibility for quantifying metabolic rates in the human brain.

Comparison of kinetic models provided quantitative and spatially-resolved maps of k_PL rates of conversion of pyruvate into lactate, which will be useful in future studies to assess the clinical importance of the method as for diagnosis and response to treatment.

Acknowledgements

References

[1] Ardenkjaer-Larsen, J. H., Fridlund, B., Gram, A., Hansson, G., Hansson, L., Lerche, M. H., Servin, R., Thaning, M. & Golman, K. Increase in signal-to-noise ratio of > 10,000 times in liquid-state NMR. Proc. Natl. Acad. Sci. U. S. A. 100, 10158–10163 (2003).

[2] Park, I., Larson, P. E. Z., Zierhut, M. L., Hu, S., Bok, R., Ozawa, T., Kurhanewicz, J., Vigneron, D. B., VandenBerg, S. R., James, C. D. & Nelson, S. J. Hyperpolarized C-13 magnetic resonance metabolic imaging: application to brain tumors. Neuro-Oncol. 12, 133–144 (2010).

[3] Nelson, S. J., Kurhanewicz, J., Vigneron, D. B., Larson, P. E. Z., Harzstark, A. L., Ferrone, M., van Criekinge, M., Chang, J. W., Bok, R., Park, I., Reed, G., Carvajal, L., Small, E. J., Munster, P., Weinberg, V. K., Ardenkjaer-Larsen, J. H., Chen, A. P., Hurd, R. E., Odegardstuen, L.-I., Robb, F. J., Tropp, J. & Murray, J. A. Metabolic Imaging of Patients with Prostate Cancer Using Hyperpolarized [1-13C]Pyruvate. Sci. Transl. Med. 5, 198ra108-198ra108 (2013).

[4] Ardenkjaer-Larsen, J. H., Leach, A. M., Clarke, N., Urbahn, J., Anderson, D. & Skloss, T. W. Dynamic nuclear polarization polarizer for sterile use intent. NMR Biomed. 24, 927–932 (2011).

[5] Gordon JW, Vigneron DB, Larson PEZ. Development of a symmetric echoplanar imaging framework for clinical translation of rapid dynamic hyperpolarized 13C imaging. Magn Reson Med. 2017;77:826–832

[6] Miller AJ, Joseph PM. The use of power images to perform quantitative analysis on low SNR MR images. Magn Reson Imaging 1993;11:1051–1056.