3552

MR image reconstruction using the Chambolle-Pock algorithm
Jing Cheng1, Sen Jia1, Haifeng Wang1, and Dong Liang1

1Shenzhen Institutes of Advanced Technology,Chinese Academy of Sciences, Shenzhen, China

Synopsis

The combination of Parallel imaging (PI) and compressed sensing (CS) allow high quality MR image reconstruction from partial k-space data. However, most CS-PI MRI methods suffer from detail loss with large acceleration and complicated parameter selection. In this work, we describe and evaluate an efficient and robust algorithm to overcome these limitations. The experimental results on in vivo data show that, the proposed method using a first-order primal-dual algorithm can successfully remove undersampling artifacts while keeping the details with little parameter tuning compared with the existing advanced method.

INTRODUCTION

CS-based MR image reconstruction is usually considered as an optimization problem which consists of the data consistency and the sparsity constraint1. Thus the final reconstructed image is highly related to the parameters in the optimization problem. In practice, the reconstruction algorithm need to tune many free parameters to have the best diagnostic image quality with the available data. For clinical applications, it is necessary to have a robust algorithm that have no or little parameters to tune. In this work, we describe and evaluate one general algorithm which is insensitive to the sole free parameter to CS-pMRI reconstruction in the TV-minimization framework. The use of this method is illustrated by applying it to in vivo brain data.

METHOD

The reconstruction of parallel MR imaging with TV regularization can be formulated as:$$\begin{cases}\min_{u}⁡‖∇u‖_1 \\s.t. Eu=f \end{cases}(1)$$where $$$u$$$ is the image we need to reconstruct, $$$E$$$ denotes the sensitivity encoding matrix, $$$f$$$ is the data acquired with arbitrary k-space sampling patterns, and $$$∇$$$ is the gradient operator.The Chambolle-Pock (CP) algorithm is a first-order primal-dual algorithm suitable for non-smooth convex optimization problems, and has been proved convergence in mathematics2. It is usually applied to a general form of the primal minimization:$$\min_{x}⁡{F(Kx)+G(x)} (2)$$and solves it simultaneously with its dual, which provides a robust convergence check – the duality gap. Therefore, we can rewrite Eq. (1) as$$\min_u⁡{‖∇u‖_1+\frac{λ}{2} ‖Eu-f‖_2^2 } (3)$$$$$λ$$$ is the regularization parameter, The whole minimization objective can be written in the form of CP algorithm with the following assignments:$$F(Kx)=‖∇x‖_1,G(x)=\frac{λ}{2} ‖Ex-f‖_2^2 (4)$$$$x=u,K=∇ (5)$$$$$G(x)$$$ is uniformly convex, hence we can use the CP algorithm to solve the MR reconstruction problem as follows:$$\begin{cases}y_{n+1}=prox_σ [F^* ](y_n+σ_n Ku ̅_n)=\frac{y_n+σ_n Ku ̅_n}{max⁡(1,y_n+σ_n Ku ̅_n)}\\u_{n+1}=prox_τ [G](u_n-τ_n K^* y_{n+1})=E^{-1} [\frac{E(u_n-τ_n K^* y_{n+1} )+τ_n λf}{1+τ_n λ}]\\θ_n=1/sqrt{(1+2γτ_n) },τ_{n+1}=θ_n τ_n,σ_{n+1}=σ_n/θ_n \\u ̅_{n+1}=u_{n+1}+θ_n (u_{n+1}-u_n)\end{cases} (6)$$where $$$τ_0=σ_0=1/L, L$$$ is the $$$l_2-norm $$$ of the matrix $$$K$$$, $$$γ$$$ is the parameter related to function $$$G$$$, $$$F^*$$$is the convex conjugate of the function $$$F$$$ which can be computed by the Legendre transform3, and the proximal mapping of the convex function $$$H(x)$$$ is obtained by the following minimization:$$prox_σ [H](x)=arg \min_{z}⁡{\left\{H(z)+\frac{‖z-x‖_2^2}{2σ}\right\}} (7)$$The proximal mapping has a closed-form representation if the function $$$H$$$ is simple.There are no other free parameters except the regularization parameter in Eq. (6). This is an important feature for our purpose of CS-pMRI reconstruction.

RESULTS

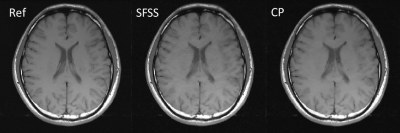
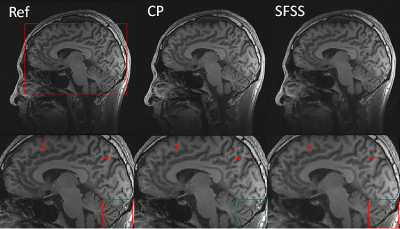
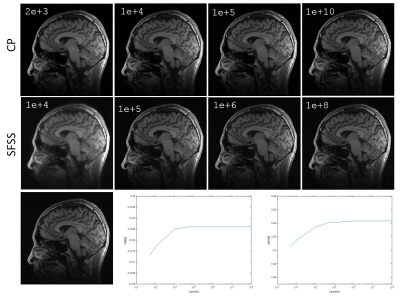
We evaluated the performance of the CP-based reconstruction method described above with two sets of in vivo human brain data and compared with self-feeding SparseSENSE (SFSS)4 , an advanced method for CS-pMRI. Different from the proposed method, SFSS requires empirical tuning of many parameters (e.g., relative weights in solving two subproblems separately). Informed consent was obtained from the imaging object in compliance with the IRB policy. The axial data set was from a 3T commercial scanner (GE Healthcare, Waukesha, WI) with an 8-channel head coil (In Vivo, Gainesville, FL) using a two-dimensional T1–weighted spin echo protocol (TE/TR = 11/700ms, 22-cm FOV, 10 slices, 256×256 matrix). The sagittal data set was acquired from the GE 3T scanner with 32-channel head coil and 3D T1-weighted spoiled gradient echo sequence, TE=minimum full, TR=7.5ms, FOV=24×24cm, matrix=256×256 and slice thickness=1.7mm. For evaluation, the sum-of-square reconstruction from full data was used as the reference, and R=4 uniform down-sampled data and R=6 Poisson disk down-sampled data were obtained manually. For R=4, the central 32 k-space lines were used for initial sensitivity calculation whereas the central 36x36 area was used for R=6. Figure 1 shows the axial data set reconstruction with different methods at the acceleration factor of R=4. For visual inspection, both methods have reduced artifacts, and demonstrate comparable image quality. Figure 2 shows the reconstructions of sagittal data containing more anatomic details for Poisson disk sampling with reduction of R=6. We observe that both methods remove noise-like artifacts, while CP method illustrates superior performance in terms of detail preserving because of the solid convergence criteria. We tested the CP method and SFSS method with different values of regularization parameter $$$λ$$$, while the rest parameters of SFSS were set to be optimal empirically. The reconstruction results are depicted in Figure 3. It has been demonstrated that the CP method appears to be totally insensitive to the value of $$$λ$$$ which can be explained in Eq. (6), and it converges well even with very large $$$λ$$$ values.

CONCLUSION

In this work, we have described a new method– CP algorithm for TV-based CS-pMRI reconstruction. The CP-based method presented here shows highly efficient reconstruction in terms of both image quality and parameter selection. Using the CP algorithm, other applications could be investigated such as other optimization-based reconstruction formulations with different image representations, objective and constraint designs, or projection models.

Acknowledgements

This work is supported in part by the National Natural Science Foundation of China under grant nos. 61401449, 61471350 and 61771463.

References

1. Liang D, Liu B, Wang J, Ying L. Accelerating SENSE using compressed sensing. Magn Reson Med 2009; 62: 1574-1584.

2. Chambolle A, Pock T. A first-order primal-dual algorithm for convex problems with applications to imaging. J. Math. Imag. Vis. 2011; vol. 40:1–26.

3. Rockafellar, RT. Convex analysis. Princeton Univ. Press; 1970.

4. Huang F, Yin W, Lin W, Ye X, Guo W, Reykowski A. A rapid and robust numerical algorithm for sensitivity encoding with sparsity constraints: Self-feeding sparse SENSE. Magn Reson Med 2010; 6(4):1078-1088.

Figures

Figure 1. Comparison of reconstruction methods for R=4. Both SFSS and CP can reduce the level of aliasing artifacts, whereas the SFSS method shows noiser than CP.

Figure 2. Comparison of reconstruction methods for R=6. The second row are the respective zoom-in images indicated by the red rectangular in the reference image. The CP method contains more features than SFSS, especially at the location indicated by the red arrows.

Figure 3. Reconstructions with different values of λ . The number on the left top of each subfigure is the value of λ. The brain image on the last row is the reference form full data and the plots are the root mean square error (RMSE) and the mean structural similarity index (mSSIM) of the reconstruction versus the values of λ. The CP method has wider range of proper parameter.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
3552