3549

Accelerating T2 Mapping Using a Self-trained Kernel PCA Model
Chaoyi Zhang1, Ukash Nakarmi1, Hongyu Li1, Yihang Zhou2, Dong Liang3, and Leslie Ying1,4

1Electrical Engineering, University at Buffalo, SUNY, Buffalo, NY, United States, 2Medical Physics and Research department, Hong Kong Sanatorium & Hospital, Happy Valley, Hong Kong, 3Biomedical and Health Engineering, Shenzhen Institutes of Advanced Technology, Shenzhen, China, 4Biomedical Engineering, University at Buffalo, SUNY, Buffalo, NY, United States

Synopsis

Kernel Principal component analysis(KPCA) model has recently been proposed to accelerate dynamic cardiac imaging. In this abstract, we study the effectiveness of KPCA for MR T2 mapping from highly under-sampled data acquired at different echo time. Different from dynamic cardiac imaging where only morphological information is needed, the quantitative values are highly important in parameter mapping. Here we use a self-trained KPCA model to guarantee the accuracy of the reconstructed T2 maps. The experimental results show that the proposed method can recover the T2 map with high fidelity at high acceleration factors.

Introduction

MR quantitative parameter mapping provides a potential quantitative tool in clinical diagnosis1, but the lengthy acquisition time limits its wide application. Several compressed-sensing(CS) based methods have been proposed to reduce the acquisition time2-11. Among these methods, principal component analysis(PCA) has been widely accepted as a good model to represent the exponential functions. In this abstract, we use kernel-PCA12 to model the nonlinearity of the exponential functions. Different from the KLR method13 for dynamic cardiac imaging where only the morphological information is needed, our proposed method uses the parametric model to train the kernel PCA so that the quantitative measures can be estimated accurately.

Method

In MR parameter mapping, the mth parameter-weighted image $$$I_{m}$$$ and the k-space data $$$d_{m}$$$ at mth measurement time can be represented as $$$d_{m}=F_{m}I_{m}+n_{m}$$$, where $$$F_{m}$$$ denotes Fourier operator with undersampling, $$$n_{m}$$$ denotes the k-space measurement noise. In the meanwhile, the images $$$I_{m}$$$ also come from a point from a parametric model: $$$I_{m}=P_{m}(\theta)\rho$$$, where $$$P_{m}(\theta)$$$ is a parametric function of θ and ρ is a linearly related constant. For example, in T2 mapping, the image at the mth measurement time is: $$$I_{m}=\rho e^{-TE(m)\theta}$$$, where θ is 1/T2. Our objective is to reconstruct the parameter map θ from the undersampled k-space data $$$d_{m}$$$ from all m. To find θ, we first reconstruct all $$$I_{m}s$$$ using KLR.

Training Using kPCA: We first construct a number of training datasets using the parametric model: $$$p_{t,m}=P_{m}(\theta t)\rho$$$ where the parameter θt take different values at different training sample t. We then perform kernel PCA on the training data. Specifically, we construct the kernel matrix $$$K_{p}$$$ whose (i,j)th element is given by $$$(<p_{ti},p_{tj}>+c)^{d}$$$, and then the principal components in the feature space is represented as $$$v_{l}=\sum_{t=1}^b\alpha_t^l\phi(p_{t})$$$, where $$$\alpha_t^l$$$ is the eigenvector of $$$K_{p}$$$.

Low Rank Enforcement in Feature Space: In this step, the zero-filled reconstruction from undersampled data is projected onto the feature space. Specifically, we construct a kernel vector between the training and testing data $$$k_{xp}=(<p_{ti},x_{q}>+c)^{b}$$$, q = 1,2,...,M, where M is the size of the image, and then find the projection coefficients $$$\beta_l^q=\alpha_l^Tk_{xp}$$$ will be calculated by projecting the $$$K_{xp}$$$ onto $$$v_{k}$$$. We assume that data can be sparsely represented by remaining only largest PCs in feature space and only K projection coefficients are calculated.

Preimaging with Data Consistency and TV Constraint: The images are then transferred back to the original data space using preimaging methods. The data consistency is enforced by replacing the values at the acquired k-space locations by the acquired values. The reconstructed image $$$I_{m}$$$ is finally smoothed using the total variation(TV) prior.

The above three steps are then repeated until convergence. Once we have all parameter-weighted images, we use Lavenberg-Marquardt algorithm to fit the parametric model and find the desired parameter map θ.

Results

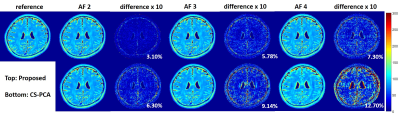
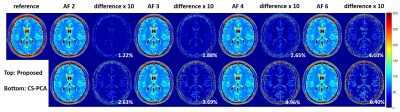
The proposed method was evaluated using two different datasets. Figure 1 shows the results from a set 6-channel T2 barin dataset from a 3T scanner(MAGNETOM Trio, SIEMENS, Germany) with a turbo spin echo sequence (matrix size = 192 × 192, FOV = 192 × 192mm, slice thickness = 3mm, ETL = 16, ΔTE = 8.8ms, TR = 4000ms, bandwidth = 362Hz/pixel). The fully acquired k-space data was retrospectively undersampled with reduction factors of 2,3 and 4 using 1D random sampling patterns, where different echoes have different patterns. Figure 2 and Figure 3 show the results from a set of phantom data with a matrix size of 218 × 182, ETL = 16, ΔTE = 8.8ms. A 1D random sampling pattern was used in Figure 2 and a 2D variable density sampling pattern in Figure3. Based on the observation, the proposed method can recover the T2 maps more accurately for both cases. We also calculated the normalized root mean square error(NRMSE) in the region-of-interest. The results showed that the NRMSE from the proposed method is less than 5%, which is much lower than the NRMSE from PCA-based compressed sensing method (CS-PCA).

Conclusion

In this abstract, we have demonstrated the effectiveness of kernel PCA as a prior model for parameter mapping from undersampled data. The model is able to characterize the nonlinearity of the relaxation function and thereby is more accurate than the linear PCA model. Experimental results show the superior of the proposed method with highly accelerated data.

Acknowledgements

This work is supported in part by the NSF CCF-1514403, NIH R21EB020861.

References

  1. Cheng LM, Stikov NS, Ghugre NR, Wright GA. Practical medical applications of quantitative MR relaxometry, J. Magn. Reson. Imag., 36:805-824, 2012.
  2. Feng L, Otazo R, Jung H, Jensen JH, Ye JC, Sodickson DK, Kim D. Accelerated cardiac T2 mapping using breath-hold multiecho fast spin-echo pulse sequence with k-t FOCUSS. Magn. Reson. Med., 65:1661–1669, 2011.
  3. Velikina JV, Alexander AL, Samsonov A, Accelerating MR parameter mapping using sparsity promoting regularization in parametric dimension, Magn. Reson. Med., 70: 1263-1273, 2013.
  4. Huang C, Graff CG, Clarkson EW, Bilgin A, Altbach MI, T2 mapping from highly undersampled data by reconstruction of principal component coefficient maps using compressed sensing, Magn. Reson. Med., 67: 1355-1366, 2012.
  5. Petzschner FH, Ponce IP, Blaimer M, Jakob PM, Breuer FA. Fast MR parameter mapping using k-t principal component analysis, Magn. Reson. Med., 66: 706-716, 2011.
  6. Zhou YH, Shi C, Wang YH, Lyu JY, Ying L, PRAIRIE: Accelerating MR Parameter Mapping Using Kernel-Based Manifold Learning and Pre-Imaging. ISMRM, 3585,2015.
  7. Doneva M, Bornert P, Eggers H, Stehning C, Senegas J, Metins A. Compressed sensing reconstruction for magnetic resonance parameter mapping. Magn. Reson. Med., 64: 1114-1120, 2010.
  8. Li W, Griswold M, Yu X. Fast cardiac T1 mapping in mice using a model-based compressed sensing method. Magn. Reson. Med., 68:1127-1134, 2012.
  9. Zhao B, Lu W, Hitchens T.K, Lam F, Ho C, Liang ZP. Accelerated MR parameter mapping with low-rank and sparsity constraints. Magn. Reson. Med., 74:489-498,2014.
  10. Zhang T, Pauly JM, Levesque IR. Accelerating parameter mapping with a locally low rank constraint. Magn. Reson. Med., 73:655–661, 2015.
  11. Sumpf TJ, Uecker M, Boretius S, Frahm J, Model-based nonlinear inverse reconstruction for T2 mapping using highly undersampled spin-echo MRI, J. Magn. Reson. Imag., 34: 420-428, 2011.
  12. B. Scholkopf, A. Smola, and K.R. Muller, “Kernel principal component analysis,” Proc. 1997 ICANN LNCS, pp. 583-588.
  13. U. Nakarmi, Y. Wang, J. Lyu, D. Liang, L. Ying, “A kernel-based low-rank (KLR) model for low-dimensional manifold recovery in highly accelerated dynamic MRI”, IEEE Transactions on Medical Imaging, Epub, July 2017

Figures

Figure 1. 6-Channel in-vivo T2 brain dataset. Estimated T2 maps and difference maps from 1D random undersampling using fully sampled data, Proposed method and CS-PCA

Figure 2. Phantom T2 brain dataset. Estimated T2 maps and difference maps from 1D random undersampling using fully sampled data, Proposed method and CS-PCA

Figure 3. Phantom T2 brain dataset. Estimated T2 maps and difference maps from 2D variable density undersampling using fully sampled data, Proposed method and CS-PCA

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
3549