Introduction:

Magnetic Resonance Fingerprinting (MRF¹) acquires a series of highly undersampled time-point images in a continuous magnetization transient state, varying sequence parameters to produce tissue specific signal evolutions (fingerprints), which are matched to previously simulated signals (dictionary). MRF k-space trajectories are designed to produce spatio-temporal incoherent aliasing, however aliasing from high undersampling factors can propagate into the parametric maps. Low rank approximations^2,3,4 in MRF enable higher acceleration factors than what initially proposed¹. In steady-state MRI approaches, locally low rank regularization has been used to further accelerate the scans^5,6,7. Here we combine low rank MRF approximation and locally low rank regularization to improve parametric map quality and achieve higher acceleration factors than the low rank approximation reconstruction. The proposed approach was evaluated in simulations and in-vivo­ brain acquisitions.

Methods:

Time-point images of an MRF series are correlated, meaning that the time series can be compressed. This temporal compression operator ($$$ \bf{U_r} $$$) can be obtained by truncating (to the appropriate rank r) a singular value decomposition of the MRF dictionary². $$$ \bf{U_r} $$$ can be combined with SENSE by solving⁴: $$$ \bf{\hat {I}} = \it{arg min}_{I} || \bf{E U_r I - K} ||_2^2 $$$ , where $$$ \bf{\hat {I}} $$$ is the temporally compressed image series, $$$ \bf{E} $$$ is the SENSE encoding operator and $$$ \bf{K} $$$ is the acquired k-space. Local low rank has been shown to be more compressible than global low rank in several applications^6,7, including parametric mapping. Here, we include a local low rank regularization term in the existing low rank approximation MRF reconstruction by solving:$$$ \bf{\hat {I}} = \it{arg min}_{I} || \bf{E U_r I - K} ||_2^2 + \lambda \sum_b {|| \bf{R_b I} ||_*} $$$ , where $$$ \bf{R_b} $$$ thresholds the singular value decomposition of an image block b and $$$ \lambda $$$ controls the regularization strength. The problem above was solved with the Alternating Direction Method of Multipliers (ADMM).

Experiments:

A digital phantom modelled after a brain image with realistic T₁ and T₂ values was used to simulate an MRF acquisition with a sequence similar to⁸. The sampling was simulated with a golden radial trajectory (one radial spoke per time-point), known sensitivity coil maps and 1750 time-points. The simulated k-space data was then undersampled uniformly in time by a factor of n (e.g. keeping [1:n:1750] k-space lines, with n = [1, 2, 3, 4]) to obtain time-point series with Nt = 1750, 875, 584 and 438 images. Three healthy subjects were scanned in a 1.5T Philips MR scanner using a 12-channel head coil and the same sequence as in simulations. Acquisition parameters included: TE/TR=1.23/4.3 ms, 1750 time-points, one spoke per time-point, resolution=2x2 mm², FOV=320x320 mm² and 10 mm slice thickness. In-vivo data was retrospectively undersampled in the same way as in simulations. All datasets were reconstructed with the low rank approximation (LrMRF) and with the locally low rank regularized low rank approximation (LLR-LrMRF). Both reconstructions had a rank r = 15. The locally low rank had a block size = 7 and local rank threshold = 5% of the maximum singular value. In both reconstructions, the regularized data consistency term was solved with the Conjugate Gradient algorithm with 15 iterations. The ADMM problem was limited to 30 iterations.

Results:

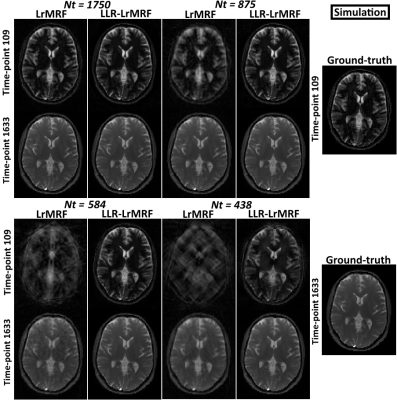
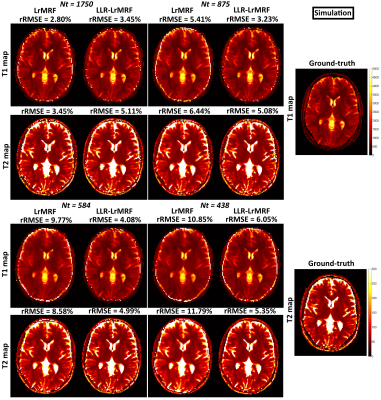
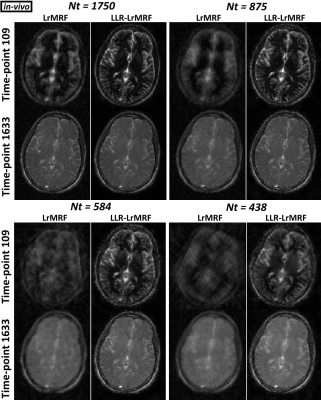
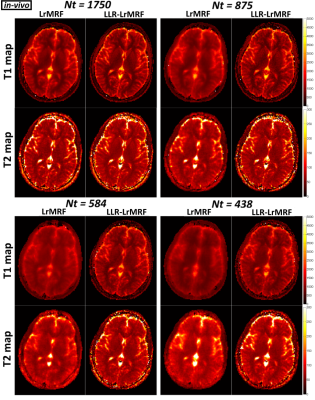
Time-point images for LrMRF and LLR-LrMRF are shown in Fig.1 for different lengths of the time-point series, in simulation. Residual aliasing artefacts can be seen in LrMRF even for 1750 time-points, which are reduced with the proposed LLR-LrMRF. Corresponding parametric maps are shown in Fig.2, where some of the artefacts present in the maps can also be seen in the time-point images. Overall these artefacts are reduced with the proposed LLR-LrMRF reconstruction, as are the root mean square relative errors of the parametric maps. Time-point images from a representative subject for different lengths of the time-point series are shown in Fig.3, in-vivo; corresponding parametric maps are shown in Fig.4. Again, residual artefacts in LrMRF are reduced with LLR-LrMRF even for 1750 time-points. LLR-LrMRF with 584 time-points achieves comparable parametric maps to LrMRF with 1750 time-points; considerable artefacts are present when only 483 images are used.

Conclusion:

A locally low rank regularization for the low rank approximation reconstruction in MRF has been introduced and validated in simulations and in-vivo. The proposed method provides parametric maps from ~600 time-point images with one radial spoke per time-point and higher quality than low rank approximation even for 1750 time-points. At reduced number of time-point images, insufficient T₁/T₂ encoding is a potential limitation. Future work will consider new encodings (sequence parameter combinations) for reduced number of time-point images and 3D acquisitions where the increased acceleration provided by the proposed approach will be essential.

Acknowledgements

This work was supported by EPSRC EP/P001009/1 and FONDECYT 1161055.