3547
Self-calibrating nonlinear MR image reconstruction algorithms for variable density sampling and parallel imaging1CEA/NeuroSpin & INRIA Parietal, Gif-sur-Yvette, France, 2CEA/NeuroSpin, Gif-sur-Yvette, France
Synopsis
Compressed Sensing has allowed a significant reduction of acquisition times in MRI. However, to maintain high signal-to-noise ratio during acquisition, CS is usually combined with parallel imaging (PI). Here, we propose a new self-calibrating MRI reconstruction framework that handles non-Cartesian CS and PI. Sensitivity maps are estimated from the data in the center of k-space while MR images are iteratively reconstructed by minimizing a nonsmooth criterion using the proximal optimized gradient method, which converges faster than FISTA. Comparison with L1-ESPIRiT suggests that our approach performs better both visually and numerically on 8-fold accelerated Human brain data collected at 7 Tesla.
Introduction
Reducing scan times in Magnetic Resonance Imaging (MRI) is essential to explore higher spatial resolution. Common methods to speed up MR acquisition rely either on deterministic or pseudo-random subsampling of k-space. This can be achieved using either parallel imaging (PI) [1] or compressed sensing (CS) [2], or both [3-4] to benefit from high SNR using a multiple receiver coil. Variable density sampling (VDS) is required to achieve high acceleration factors in MRI scans [1,5-6]. In prospective CS, VDS is implemented along non-Cartesian k-space trajectories (radial, spiral, …). Although recent CS-PI reconstruction algorithms [4,7] are able to deal with multichannel non-Cartesian data, they usually proceed with a gridding step [8] to get a Cartesian k-space before performing MR image reconstruction. Here, we propose a new self-calibrating approach to MR image reconstruction in the CS-PI context. An automated and fast procedure for extracting the sensitivity maps is proposed using the original non-Cartesian data and the Nonequispaced fast Fourier transform (NFFT) [9]. Second, we implement the Proximal Optimized Gradient Method (POGM) to solve the CS-PI reconstruction problem. To illustrate its advantages over ESPIRiT [10], the proposed method is tested to reconstruct high resolution 2D T2* images from 8-fold undersampled variable-density Sparkling [11] data at 7 Tesla using a 32-channel receiver coil.Materials and Methods
Setup. Four healthy volunteers were scanned with a 7T system (Siemens Healthineers, Erlangen, Germany) and a 1Tx/32Rx head coil (Nova Medical, Wilmington, USA). All subjects signed a written informed consent form and were enrolled in the study under the approval of our institutional review board.
Sequence and k-space trajectories. A modified 2D T2*-weighted interleaved GRE sequence was acquired for an in-plane resolution of 390 ㎛ with the following parameters: TR=550ms, TE=30ms and FA=25° for one axial slice of 3 mm-thickness, matrix size N=512x512. The Sparkling trajectory (Fig. 1) was composed of 64 shots, each comprising 512 samples during a readout of 30.72 ms. Although Sparkling was implemented prospectively, here we used this sampling scheme retrospectively from fully sampled Cartesian data. Hence, the number of measurements was M=32,768 and the subsampling factor R=N/M=8.
Sensitivity
maps extraction. Sensitivity
maps information lies in the low-frequency domain, hence
variable-density trajectories like radial or sparkling intrinsically
handle this information and allow self-calibration without fully
sampling the k-space center. Our sensitivity map estimation method
thus extracts the 10% central surface of the measured k-space. Then,
low frequency NxN coil images were reconstructed applying the NFFT
operator to the data completed by zero-filling. Third, the square
root of the Sum of Squares (SSOS) was computed. Fourth, the
sensitivity maps were estimated by the pixelwise ratio between image
coils and the SSOS.
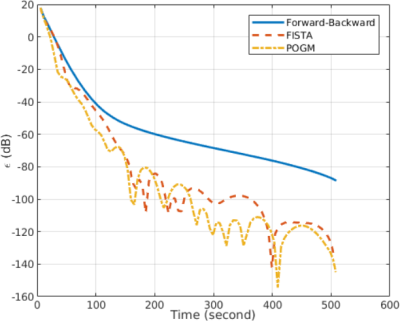
Reconstruction. The CS-PI reconstruction problem consists of minimizing a penalized least square criterion involving the data collected over the 32 channels and a L1-norm penalty term promoting sparsity in the wavelet domain. The balance between the two is controlled by paramter λ>0 whose optimal setting was performed using a grid search procedure over [10-7, 10-4]. Forward-Backward, FISTA and POGM optimization algorithms are summarized in Fig. 2.
Results
Sensitivity maps. Fig. 3 illustrates three sensitivity maps extracted using either our method or L1-ESPIRIT. Because of the SVD decomposition involved in L1-ESPIRIT, the sensitivity profiles are smoother as compared to ours, which clearly delineate the FOV part illuminated by each receiver coil. Moreover, our approach is faster since it costs 1min as compared to 10min for L1-ESPIRIT on the same architecture and Matlab-R2017 software.
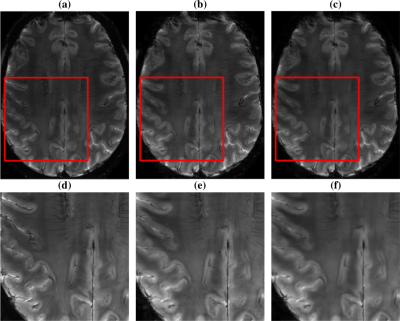
MR image reconstruction. MR images were reconstructed from Sparkling data either using our approach or L1-ESPIRiT. Although full FOV images look very similar (Fig. 4(a)-(c)), the respective zooms (Fig. 4(d)-(f)) show that the dark stripes in the white matter are lost in the L1-ESPIRiT image whereas they are well preserved using our self-calibrating solution. In addition, our POGM algorithm converged in 2.5 min whereas L1-ESPIRiT took about 5 min.
Convergence
speed. The
same experimental setup was used to compare the three algorithms. As
reported in Fig.
5,
FISTA and POGM decrease faster than FB even though they show some
“Nesterov ripples”. Interestingly, POGM decreases a little bit
faster than FISTA during the first tens of iterations.
Discussion and Conclusion
Compared to the state-of-the-art, the proposed self-calibrating method to the CS-PI reconstruction problem is more efficient and the sensitivity profiles are easier to interpret. Based on these estimates, we have shown that POGM converges faster than FB and FISTA. On in vivo Human brain T2* data collected at 7 Tesla, we have also demonstrated that our approach is both more accurate and efficient than L1-ESPIRiT. Future work will be devoted to further speed up reconstruction by coupling POGM with B1-based surrogates as proposed in [12] for FISTA in Cartesian acquisition scenarios.Acknowledgements
We would like to thank Prof. Jeffrey Fessler who provided significant insight during his stay at NeuroSpin in June 2017. This research program was supported by DRF Impulsion grant in 2016 (COSMIC, P.I.: P.C.).References
[1]: Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. (1999). SENSE: sensitivity encoding for fast MRI. Magnetic Resonance in Medicine. 42(5):952-62. [2]: Lustig M, Donoho D, Pauly JM. (2007). Sparse MRI: The application of compressed sensing for rapid MR imaging. Magnetic Resonance in Medicine. 58(6):1182-95. [3]: Liang D, Liu B, Wang J,Ying L (2009). Accelerating SENSE using compressed sensing. Magnetic Resonance in Medicine. 62(6):1574-84. [4]: Chun IY, Adcock B, Talavage TM,Ying L (2016). Efficient compressed sensing pMRI reconstruction with joint sparsity promotion. IEEE Transactions on Medical Imaging. 35(1):354-68. [5]: Puy G, Vandergheynst P, Wiaux Y (2011). On variable density compressive sampling. IEEE Transactions on Signal Processing Letters. 18(10): 595-98. [6]: Chauffert N, Ciuciu P, and Weiss P (2014).Variable density sampling with continuous trajectories. Application to MRI. Siam Imaging Science. 7(4):1962-92. [7]: Lustig M, Pauly JM. SPIRiT (2010): Iterative self‐consistent parallel imaging reconstruction from arbitrary k‐space. Magnetic Resonance in Medicine. 64(2):457-71. [8]: Beatty PJ, Nishimura DG, Pauly JM (2005). Rapid gridding reconstruction with a minimal oversampling ratio. IEEE transactions on medical imaging. 24(6):799-808. [9]: Keiner J, Kunis S, Potts S (2009). Using NFFT 3 – a software library for various nonequispaced fast Fourier transforms. ACM Transactions on Mathematical Software. 36(4):19. [10]: Uecker M, Lai P, Murphy MJ, Virtue P, Elad M, Pauly JM, Vasanawala SS, Lustig M (2014). ESPIRiT— an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magnetic Resonance in Medicine. 71(3):990-1001. [11]: Lazarus C, Weiss P, Chauffert N, Mauconduit F, Bottlaender M, Vignaud A, Ciuciu P (2017). SPARKLING: Novel non-Cartesian sampling schemes for accelerated 2D anatomical imaging at 7 T using compressed sensing. 25th Proceedings of the ISMRM. Honolulu, Hawaii, USA. [12]: Muckley MJ, Noll DC, Fessler JA. Fast parallel MR image reconstruction via B1-based, adaptive restart, iterative soft thresholding algorithms (BARISTA) (2015). IEEE Transactions on Medical iImaging. 34(2):578-88.Figures
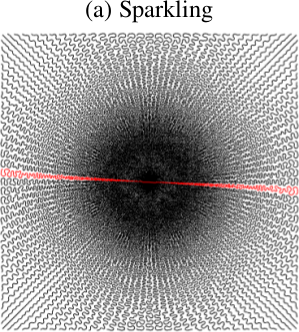

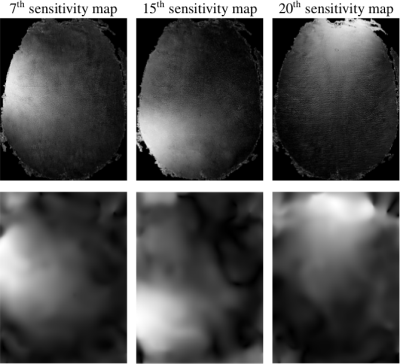
Fig. 3: Estimation of sensitivity maps. Top: 3 out of 32 sensitivity maps extracted using our method. Bottom: Three consistent sensitivity maps yielded by the ESPIRiT algorithm based on eigenvalue decomposition.