3545
Synergistic reconstruction of undersampled multi-contrast MRI using weighted quadratic priors1School of Biomedical Engineering and Imaging Sciences, King’s College London, London, United Kingdom, 2MR Research Collaborations, Siemens Healthcare Limited, Frimley, United Kingdom, 3School of Biomedical Engineering and Imaging Sciences, King’s College London & Guy’s and St Thomas’ PET Centre, London, United Kingdom
Synopsis
We propose a simple and robust methodology for synergistic multi-contrast MR image reconstruction to improve image quality of undersampled MR data beyond what is achieved from conventional independent reconstruction methods. The advantages of the proposed methodology are threefold: i) it exploits quadratic priors that are mutually weighted using all available MR images, leading to preservation of unique features, ii) the weighting coefficients are independent of the relative signal intensity and contrast of different MR images and iii) the algorithm is based on a well-established parallel imaging iterative reconstruction, which makes the synergistic reconstruction of undersampled MR data clinically feasible
Introduction
MR data acquisition is often time consuming, particularly in multi-contrast MR protocols. Partial Fourier and parallel imaging (e.g. sensitivity encoding –SENSE) are conventionally employed to reduce scan time by acquiring less k-space data than established by the Nyquist criterion. Compressed sensing (CS) exploits the sparsity of the images in a given domain to further reduce the acquisition time [1]. However, most of these approaches reconstruct each contrast image independently, without taking advantage of the redundant information in the multi-contrast direction. In this work, we propose a framework for synergistic reconstruction of highly undersampled multi-contrast MR data for improving upon independent parallel imaging CS (i.e. total variation– TV– regularised SENSE) reconstructions.Methods
Synergistic SENSE reconstruction of $$$n$$$ undersampled MR contrasts,$$${\boldsymbol{v}}^{\left(k\right)}$$$, is given by the following minimization problem $${\left({\widehat{\boldsymbol{v}}}^{\left(1\right)},\dots ,{\widehat{\boldsymbol{v}}}^{\left(n\right)}\right)=\mathop{\mathrm{argmin}}_{{\boldsymbol{v}}^{\left(1\right)},\dots ,{\boldsymbol{v}}^{\left(n\right)}} \left\{\sum^n_{k=1}{{\left\|{\boldsymbol{E}}^{\left(k\right)}{\boldsymbol{v}}^{\left(k\right)}\mathrm{-}{\boldsymbol{s}}^{\left(k\right)}\right\|}^2_{{\boldsymbol{W}}^{\left(k\right)}}}\mathrm{+}\frac{{\beta }_k}{2}{\left\|{\boldsymbol{D}}^{(k)}{\boldsymbol{v}}^{\left(k\right)}\right\|}^2_{{\boldsymbol{\xi }}^{(k)}{\boldsymbol{\omega }}^{(k)}}\right\}\ }\ $$
where the first term includes $$$n$$$ data fidelity terms and the second term is a multi-modal weighted quadratic penalty function. $$${\boldsymbol{E}}^{\left(k\right)}$$$ includes coil sensitivity maps and k-space undersampling trajectories of $$$\textit{k}$$$th image contrast. $$${\boldsymbol{s}}^{\left(k\right)}$$$ is the acquired k-space data, $$${\boldsymbol{W}}^{\left(k\right)}$$$ is the noise-correlation matrix between coil channels, $$${\boldsymbol{D}}^{(k)}$$$ calculates intensity differences between voxels of the $$$\textit{k}$$$th image in a local neighbourhood, the elements of $$${\boldsymbol{\xi }}^{(k)}$$$ weight these voxel differences based on their distance.$$$\ {\beta }_k$$$ are regularization parameters. The elements of $$${\boldsymbol{\omega }}^{(k)}$$$ weight the difference between voxel $$$\textit{j}$$$ and $$$\textit{b}$$$ of the$$$ \textit{k}$$$th image in a local neighbourhood based on the product of Gaussian similarity coefficients derived from all $$$n$$$ MR images, defined as:
$${\omega }^{\ }_{jb}=\frac{\mathcal{G}\left({\tilde{v}}^{\left(1\right)}_j,{\tilde{v}}^{\left(1\right)}_b,{\sigma }_1\right)\dots \mathcal{G}\left({\tilde{v}}^{\left(n\right)}_j,{\tilde{v}}^{\left(n\right)}_b,{\sigma }_n\right)}{\sum^N_{j=1}{\mathcal{G}\left({\tilde{v}}^{\left(1\right)}_j,{\tilde{v}}^{\left(1\right)}_b,{\sigma }_1\right)}\dots \mathcal{G}\left({\tilde{v}}^{\left(n\right)}_j,{\tilde{v}}^{\left(n\right)}_b,{\sigma }_n\right)} \ \mathcal{G}\left(q,r,\sigma \right)=\frac{1}{\sqrt{2\pi }\sigma }{\mathrm{exp} \left(-\frac{{\left(q-r\right)}^2}{2{\sigma }^2}\right)\ }$$
As a result, Tikhonov regularization of the $$$\textit{k}$$$th image is guided by itself and the complementary information available in other image contrasts. For the calculation of the $$$\boldsymbol{\omega }$$$ coefficients, MR contrast images are mutually registered during their reconstruction. The minimization problem was solved using the conjugate gradient (CG) algorithm for each MR contrast at each iteration (implemented in MATLAB), using the $$$\boldsymbol{\omega }$$$ derived from all images from the previous iteration, i.e. $$$\widetilde{\boldsymbol{v}}$$$. The proposed algorithm was compared to iterative SENSE and TV regularized SENSE (TV-SENSE) reconstructions, optimized using the alternating direction method of multipliers and CG algorithms.
Experiments
A patient with suspected mild cognitive impairment was scanned on a 3T Biograph mMR scanner (Siemens Healthcare, Erlangen, Germany). Acquisitions were performed for a 3D fully sampled T1-MPRAGE (resolution = 1.05$$$\times$$$1.05$$$\times$$$1.1 mm$$${}^{3}$$$, FOV = 235$$$\times$$$269$$$\times$$$191 mm$$${}^{3}$$$, TR/TE/TI = 1700/2.63/900 ms, flip-angle = 9º) and a 2x accelerated 3D FLAIR (resolution = 0.48$$$\times$$$0.48$$$\times$$$1.0 mm$$${}^{3}$$$, FOV = 245$$$\times$$$245$$$\times$$$160 mm$$${}^{3}$$$, TR/TE/TI = 5000/395/1800 ms, flip-angle = 120º) sequence. The k-space of the T1 data was retrospectively undersampled in the phase and slice encoding directions by factors of 3 and 3 (R = 9). Similarly, the FLAIR data was retrospectively undersampled by factors of 2 and 3 (R = 6)Results
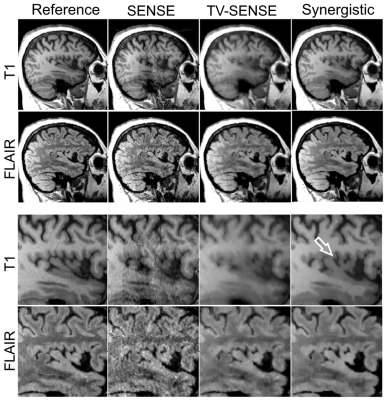
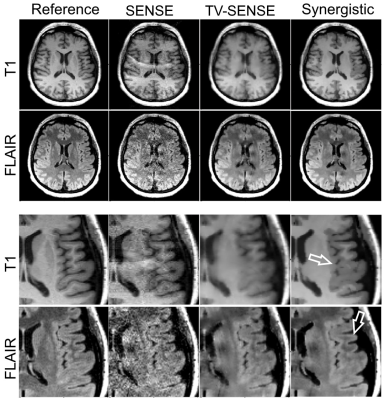
Fig. 1 and 2 shows the results of synergistic reconstruction of undersampled MR data, in comparison with fully sampled T1 and 2x undersampled FLAIR, as reference reconstructions. SENSE and TV-SENSE reconstructions are also shown for the undersampled dataset (T1: R = 9, FLAIR: R = 6). The results show that TV-SENSE reduces aliasing artefacts however at the expense of blurring in the T1 image and residual artefacts in the FLAIR image. As shown by the arrows, synergistic reconstruction of the undersampled datasets reduces noise amplification and remaining artefacts, and enhances the edges, especially in the FLAIR imageDiscussion
Compared to previous reference-guided and joint reconstruction methods [2,3], our proposed algorithm has a number of advantages, i) the weighting coefficients are derived from all available MR images, which leads to preservation of unique features. This should be advantageous in the case of lesions visible only on certain sequences; ii) the weighting coefficients are independent of the relative signal intensity and contrast of different MR sequences, iii) the reconstruction algorithm is based on a widely used parallel imaging algorithm. In addition, if one of the datasets is fully-sampled, the synergistic reconstruction will still be beneficial for undersampled datasets due to the preservation of unique features.Conclusions
The proposed synergistic reconstruction methodology aims to improve MR image quality by utilizing the boundary information common to different MR image contrasts and to provide a clinically feasible reconstruction algorithm. Our results using in-vivo data show the improved performance of the proposed method compared to standard separate reconstructions, therefore opening the way for more advanced reconstruction of undersampled data in routine practiceAcknowledgements
This work is supported by the Engineering and Physical Sciences Research Council (EPSRC) under grant EP/M020142/1 and the Welcome EPSRC Centre for Medical Engineering at King’s College London (WT 203148/Z/16/Z). The authors acknowledge financial support from the Department of Health via the National Institute for Health Research (NIHR) comprehensive Biomedical Research Centre award to Guy's & St Thomas' NHS Foundation Trust in partnership with King's College London and King’s College Hospital NHS Foundation Trust.References
[1] Lustig M, Magn Reson Med. 2007, 58(6):1182-95.
[2] Ehrhardt MJ and Betcke MM SIAM J. Imaging Sciences, 2015, 9(3): 1084–1106.
[3] Bilgic B, et al. Magn. Reson. Med. 2011;66:1601–1615.