3543
Rapid Parallel MRI Reconstruction Utilizing the Wavelet Filter Bank1Department of Biomedical Engineering, Technion - Israel Institute of Technology, Haifa, Israel, 2Department of Radiology, Leiden University, Leiden, Netherlands
Synopsis
A novel method for reconstruction from highly undersampled parallel MRI data is proposed. The method computes the Stationary Wavelet Transform (SWT) of the unknown MR image directly from sub-sampled k-space measurements, and then recovers the image using the Inverse SWT filter bank. Experiments with in-vivo data show that this method produces high quality reconstructions, comparable to Compressed Sensing (CS) reconstructions. However, unlike CS, the proposed method is non-iterative. Moreover, it is simple, fast, and allows flexible (random or ordered) k-space undersampling schemes.
Purpose
Parallel Imaging (PI) and Compressed Sensing (CS) are two well-established approaches for image reconstruction from undersampled k-space data. CS-MRI methods offer high k-space undersampling, using random schemes, at the price of time-intensive iterative computations; these computations repetitive implementations of forward and inverse transforms of two types, the Fourier transform and a sparsifying transform. PI methods enable rapid ordered sampling trajectories and faster computations; however they commonly do not exploit the benefits offered by non-Fourier transforms. This work introduces a novel PI reconstruction method that offers fast non-iterative computations, is suitable for arbitrary undersampling of a Cartesian k-space, and operates in the Stationary Wavelet Transform (SWT) domain.Theory
The proposed PI method consists of two steps: (i) computation of the full SWT decomposition of the unknown MR image directly from the sub-sampled k-space data, and (ii) image reconstruction by implementation of the Inverse Stationary Wavelet Transform (ISWT) filter bank.
The method exploits the theory of convolution-image computation1 for parallel multi-coil acquisition. Essentially, given k-space data sub-sampled along columns (or rows), this theory allows the computation of the convolution between the unknown MR image $$$f(x,y)$$$ and a user defined kernel $$$g(x)$$$, i.e.
$$ h(x,y)=f(x,y)*g(x).$$
In step (i) of the proposed method, this equation is implemented separately with two kernels corresponding to the first-level SWT filters of an analysis filter bank2. In other words, $$$g(x)$$$ is first defined as the Low-Pass Decomposition (LPD) filter and $$$h^{LP}(x,y)=f(x,y)*g^{LPD}(x)$$$ is computed. Secondly, $$$g(x)$$$ is defined as the High-Pass Decomposition (HPD) filter, and $$$h^{HP}(x,y)=f(x,y)*g^{HPD}(x)$$$ is computed. By definition2, these computations produce the first-level approximation and details coefficients of the 1D SWT of $$$f(x,y)$$$, where the transform is performed along rows.
In step (ii) of the proposed method, $$$f(x,y)$$$ is reconstructed by the ISWT, i.e. through the synthesis filter bank. In this process, the Low-Pass Reconstruction (LPR) filter $$$g^{LPR}(x)$$$ and High-Pass Reconstruction (HPR) filter $$$g^{HPR}(x)$$$ are applied to $$$h^{LP}(x,y)$$$ and $$$h^{HP}(x,y)$$$ correspondingly, and the results are summed, producing the reconstructed image,
$$f^{rec}(x,y)=h^{LP}(x,y)*g^{LPR}(x)+h^{HP}(x,y)*g^{HPR}(x).$$
According to the wavelet filter bank theory, the two decomposition filters $$$g^{LPD}(x)$$$, $$$g^{HPD}(x)$$$ and the two synthesis filters $$$g^{LPR}(x)$$$, $$$g^{HPR}(x)$$$ form together a two-channel quadrature mirror filter bank.
Methods
The proposed method was implemented on in-vivo data from two T1-weighted-7Tesla scans of a healthy volunteer using a 32 coil receive array. Sensitivity maps were estimated from low-resolution pre-scans. After acquiring high-resolution scans, k-space data were retrospectively sub-sampled in one dimension with a reduction factor $$$R=4$$$. The proposed method was implemented with the SWT Daubchies-2 wavelet filter bank and an additional single-step soft-thresholding for denoising. Results of this method were compared with those of a recent CS method that utilizes the SWT3. All reconstructions were compared to a gold standard reconstruction (from a fully sampled k-space) by using the NRMSE measure.Results
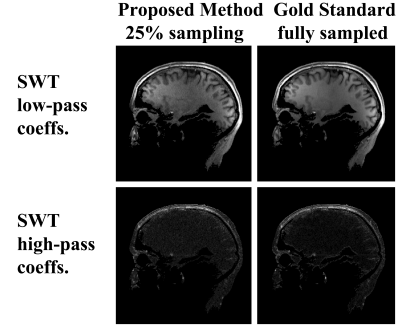
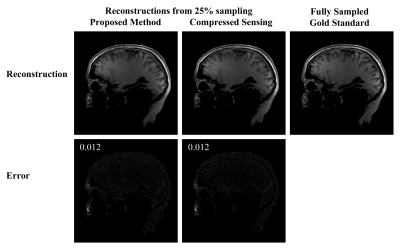
Figure 1 demonstrates the SWT coefficients computed from the in-vivo data. It includes the approximation (low-pass) and details (high-pass) coefficients computed from 25% of k-space data by the proposed method (left column), and those computed from the fully sampled data (right column). Clearly, our method produced a highly accurate reconstruction of the SWT coefficients. Figure 2 shows the final image reconstructions of the same data set. The proposed method produced an image which includes all the anatomical structures that are present in the gold standard image, without discernible artifacts. This excellent reconstruction quality is reflected by the low NRMSE value of 0.012. It is also apparent from figure 2 that our single-step method produced a reconstruction very similar to the CS reconstruction, while the latter method required 24 iterations for convergence.
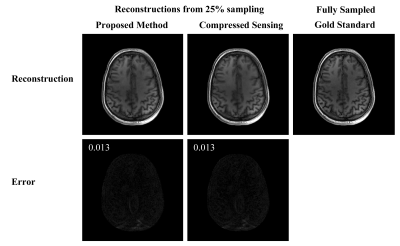
Similar high-quality results were obtained in a second in-vivo experiment (figure 3). Our proposed method produced an image similar to the gold standard and to the CS reconstruction. In this case, the CS process required 85 iterations for convergence to the same NRMSE level obtained by our single-step method.
Disccusion & Conclusion
This work introduces a novel parallel MRI method that utilizes efficient wavelet-domain processing. This method reconstructs the SWT coefficients of the unknown MR image directly from highly undersampled k-space data, and then reconstructs the image using the ISWT filter bank.
The proposed method offers the following advantages: (1) a non-iterative reconstruction process, which yields results comparable to those of an iterative CS reconstruction, (2) flexible arbitrary undersampling of a Cartesian k-space, and (3) efficient data processing in the redundant SWT domain. Due to its simplicity and fast implementation, the proposed method may be highly suitable for real-time MRI applications.
Acknowledgements
No acknowledgement found.References
1. Azhari H, Sodickson DK, Edelman RR. Rapid MR imaging by sensitivity profile indexing and deconvolution reconstruction (SPID). Magnetic Resonance Imaging. 2003;21(6):575–584.
2. Mallat SG. A wavelet tour of signal processing. Academic Press; 1999.
3. Kayvanrad MH, McLeod AJ, Baxter JSH, McKenzie CA, Peters TM. Stationary wavelet transform for under-sampled MRI reconstruction. Magnetic Resonance Imaging. 2014;32(10):1353–1364.
Figures