3539

On the importance of adapting compressed sensing for images with significant spatial phase variations
Jérémie P. Fouquet1, Michael Paquette2, Réjean Lebel1, Maxime Descoteaux2, and Martin Lepage1

1Centre d'imagerie moléculaire de Sherbrooke, department of Médecine nucléaire et radiobiologie, Université de Sherbrooke, Sherbrooke, QC, Canada, 2Sherbrooke Connectivity Imaging Lab (SCIL), Computer Science Department, Université de Sherbrooke, Sherbrooke, QC, Canada

Synopsis

We explore the limits of compressed sensing (CS) in the practical setting of T2*-weighted imaging of the brain. Surprisingly, those limits are rapidly reached due in part to the presence of spatial phase variations. While conventional CS performs well for synthetic phase-free images, it is equally performant to or even outperformed by a simple zero-padding of the k-space center for acquired complex-valued images. Clearly, CS must be adapted to images including spatial phase variations, and our results point toward new solutions to achieve this adaptation.

Introduction

Compressed sensing (CS) was shown to be an efficient method to reduce the data required to produce a magnetic resonance (MR) image with minimal quality loss1–3. It has however been reported that spatial phase variations in MR images could reduce the efficiency of CS1,4,5. In this abstract, we explore the limits of conventional CS when applied to T2*-weighted brain images. Surprisingly, we find that those limits are rapidly reached. While the underperformance of CS for images including phase variations is usually attributed to poor compressibility in the sparse basis1,4–6, we show that the k-space sampling pattern also plays an important role.

Methods

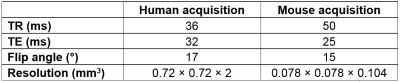
Images of human and mouse brain were acquired on a Philips Ingenia 3T scanner and a preclinical Varian 7T scanner, respectively. The k-space of T2*-weighted 3D gradient echo cartesian sequences was fully acquired. Acquisition parameters are presented in Table 1. To disentangle the effects of CS from the effects of parallel imaging, we used a single receiver coil on both scanners.

For conventional CS, we used an adaptation of the conjugate gradient algorithm provided by Lustig et al. to minimize the unconstrained formulation of CS7. We tested a 2D variable density sampling pattern defined by 1) the standard deviation of a centered gaussian giving the variable density probability function ($$$\sigma_u$$$), and 2) the diameter of a fully sampled cylinder at the center of k-space ($$$d_{FS}$$$). Both $$$\sigma_u$$$ and $$$d_{FS}$$$ were expressed as a percentage of the total k-space size. They were varied between 5% and 85%, and 5% and 45%, respectively. All undersampling patterns tested were applied retrospectively on two slices of three mouse data sets and on one slice of one human data set. We used CDF 9/7 wavelets as the sparsifying transform8 and an acceleration factor of 2.

To isolate the effect of phase, we compared the performance of conventional CS for acquired k-space data and for synthetic k-space data. Synthetic k-space data were obtained by taking the Fourier transform of the magnitude images.

To quantify the quality of the reconstructed images, two reference-based quality metrics were computed in the brain: peak signal to noise ratio (PSNR) and mean structural similarity (MSSIM)9. The magnitude of the images is used to compute the metrics.

We also tested the use of 1) an additional total variation penalty, 2) a phase correction using the center of the k-space1, 3) a Poisson disk sampling strategy, and 4) different weights for promoting sparsity during the reconstruction. While some of these modifications improved quality metrics, they did not change the conclusions on conventional CS and are therefore not presented.

Results and Discussion

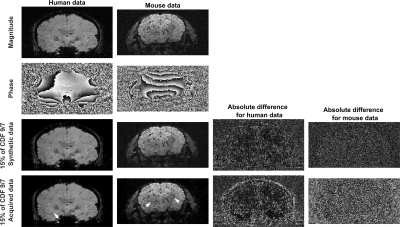
In line with previous reports1,4–6, the presence of spatial phase variations reduces the compressibility of the MR images in a conventional sparsifying transform (Figure 1). However, the images including phase still show an interesting compressibility, which could be exploited for CS reconstruction.

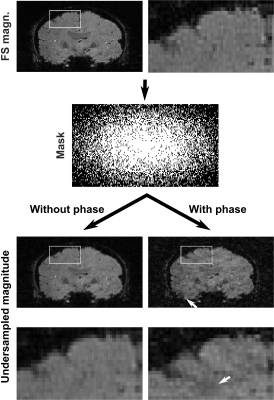
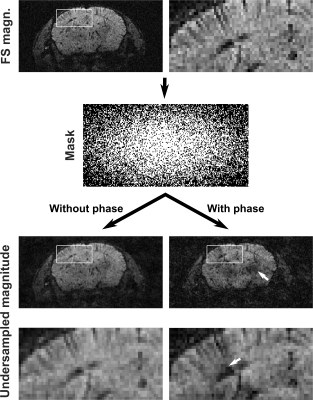
Conventional CS performs well for the synthetic k-space data representing phase-free images. Quality metrics are optimal for sampling patterns spread over k-space, with a variable density favoring points near the center (Figure 2).

The situation is very different when phase is considered: the optimal sampling pattern tends toward a fully sampled and centered ellipse. In this scenario, the quality metrics are mostly determined by the undersampling step (the CS reconstruction is not able to recover the value of the k-space points located outside the fully sampled ellipse). In other words, zero-padding a fully sampled ellipse in the center of the k-space yields better quality metrics than using a spread variable density sampling pattern with CS reconstruction. This was found to be true for both mouse (Figure 2) and human (not shown) data sets.

A randomly spread sampling pattern differently affects synthetic and acquired data sets (Figures 3 and 4). For synthetic images, it introduces artifacts resembling white noise, which is ideal for CS reconstruction. For acquired complex-valued images, it introduces coherent artifacts, which are difficult to eliminate by CS reconstruction.

Conclusion

T2*-weighted images of human and mouse brain include spatial phase variations that hamper conventional CS reconstruction to the point that simply zero-padding the k-space becomes advantageous. The CS process must therefore be optimized against the expected data. This can be done at the level of the sparse basis used1,4,5,10, but also at the level of the sampling pattern. We are now performing tests with sampling patterns adapted to both the data and the CS reconstruction strategy11,12. It would also be relevant to test more sophisticated options for phase correction13,14.

Acknowledgements

Jérémie P. Fouquet is supported by a NSERC scholarship. The authors thank Luc Tremblay and Guillaume Gilbert for MR acquisitions, and Mélanie Archambault for animal manipulation. This work was funded by CIHR.

References

1. Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn. Reson. Med. 2007;58(6):1182–1195.

2. Geethanath S, Reddy R, Konar AS, et al. Compressed Sensing MRI: A Review. Crit. Rev. Biomed. Eng. 2013;41(3):183–204.

3. Jaspan ON, Fleysher R, Lipton ML. Compressed sensing MRI: a review of the clinical literature. Br. J. Radiol. 2015;88(1056):20150487.

4. Zibetti MVW, de Pierro AR. Improving compressive sensing in MRI with separate magnitude and phase priors. Multidimens. Syst. Signal Process. 2016:1–23.

5. Feng Zhao, Noll DC, Nielsen J-F, et al. Separate Magnitude and Phase Regularization via Compressed Sensing. IEEE Trans. Med. Imaging. 2012;31(9):1713–1723.

6. Nakarmi U, Prasad S, Ying L, et al. Compressed Sensing (CS) in phase imaging requires dedicated reconstruction strategies. Proc. Intl. Soc. Mag. Reson. Med. 2015;23(4):3329.

7. Lustig M. Software: Sparse MRI. www.eecs.berkeley.edu/~mlustig/Software.html. Accessed on January 1st, 2014.

8. Mallat S. A Wavelet Tour of Signal Processing: The Sparse Way. 3rd ed. Elsevier Science; 2008.

9. Wang Z, Bovik AC, Sheikh HR, et al. Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process. 2004;13(4):600–612.

10. Ravishankar S, Bresler Y. MR image reconstruction from highly undersampled k-space data by dictionary learning. IEEE Trans. Med. Imaging. 2011;30(5):1028–1041.

11. Ravishankar S, Bresler Y. Adaptive sampling design for compressed sensing MRI. 2011 Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 2011:3751–3755.

12. Seeger M, Nickisch H, Pohmann R, et al. Optimization of k-space trajectories for compressed sensing by Bayesian experimental design. Magn. Reson. Med. 2010;63(1):116–126.

13. Pizzolato M, Fick R, Boutelier T, et al. Noise Floor Removal via Phase Correction of Complex Diffusion-Weighted Images: Influence on DTI and q-Space Metrics. In: Fuster A, Ghosh A, Kaden E, et al., eds. Computational Diffusion MRI: MICCAI Workshop, Athens, Greece, October 2016. Cham: Springer International Publishing; 2016:21–34.

14. Eichner C, Cauley SF, Cohen-Adad J, et al. Real diffusion-weighted MRI enabling true signal averaging and increased diffusion contrast. Neuroimage. 2015;122:373–384.

Figures

Table 1 - MR parameters used for human and mouse 3D gradient echo acquisitions.

Figure 1 - Compressibility of human and mouse data sets used for CS reconstruction. The first two rows show the magnitude and the phase of fully-sampled data. When 15% of the largest coefficients in the CDF 9/7 basis are retained, more artifacts are present for acquired complex images (white arrows, last row) than for synthetic (magnitude only) images (third row). This indicates that the magnitude images are more compressible in the CDF 9/7 basis than the complex images. The absolute difference between the original magnitude and the magnitude of the wavelet-thresholded images is presented in the last two columns.

Figure 2 - Optimization of the sampling pattern in the presence of phase. a) Quality metrics obtained by CS reconstruction for synthetic k-space (first column) and acquired k-space (second column) for a mouse brain image and for different sampling pattern parameters. Both MSSIM and PSNR yield similar patterns. b) Sampling pattern corresponding to the maximal MSSIM obtained in a). There is an evident shift toward center-focused patterns for acquired data. These results correspond to a single slice of a mouse brain image, but they are similar for all animal and human tested data sets.

Figure 3 - Effects of a spread undersampling pattern on the magnitude of synthetic (phase-free) and acquired human brain images. When no phase is present in the image, the undersampling produces incoherent artifacts (left column). When phase variations are present, the undersampling yields coherent artifacts, as indicated by white arrows (right column). FS magn.: fully-sampled magnitude.

Figure 4 - Effects of a spread undersampling pattern on the magnitude of synthetic (phase-free) and acquired mouse brain images. When no phase is present in the image, the undersampling produces incoherent artifacts (left column). When phase variations are present, the undersampling yields coherent artifacts, as indicated by white arrows (right column). FS magn.: fully-sampled magnitude.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
3539