3535
Joint Sparse Reconstruction of Multi-contrast MRI Images with Graph Wavelets1Department of Electronic Science, Xiamen University, Xiamen, China, 2School of Computer and Information Engineering, Xiamen University of Technology, Xiamen, China
Synopsis
Multi-contrast images in magnetic resonance imaging (MRI) are widely applied in clinical applications, since an abundant contrast information reflects the characteristics of the internal tissue of human body, providing an effective reference for clinical diagnosis. However, long acquisition time limits the application of magnetic resonance multi contrast imaging. Under-sampling the k-space data and reconstructing images with sparsity constraint is one efficient way to accelerate magnetic resonance imaging sampling. In this work, multi-contrast undersampled MRI images are jointly reconstructed under the sparse representation using graph wavelets. Experiment results demonstrate that the proposed method outperforms the compared state-of-the-art methods.
Purpose
Multi-contrast magnetic resonance imaging (MRI), reflecting the characteristics of internal organic and tissue in human body, plays an important role in clinic. However, long scanning time limits the application of multi-contrast imaging in clinic. Therefore, accelerating the multi-contrast imaging speed without missing image structures is of great significance. Under-sampling the k-space data and reconstructing the image with sparsity constraint is one of efficient ways to reduce the data acquisition time 1-4. In this work, we propose a new approach to jointly reconstruct the undersampled multi-contrast magnetic resonance images by regularizing images’ joint sparsity under the graph-based redundant wavelets representation.Methods
The under-sampling of k-space data in MRI imaging can be expressed as: $$$\mathbf{y}={{\mathbf{F}}_{\mathbf{U}}}\mathbf{x}+\boldsymbol{\varepsilon }$$$, where $$$\mathbf{\varepsilon }$$$ denotes the noise contained in k-space data; $$$\mathbf{x}={{\left[ {{\mathbf{x}}_{1}},\cdots {{\mathbf{x}}_{C}} \right]}^{T}}$$$ the column vector formed by multi-contrast images; $$$\mathbf{y}={{\left[ {{\mathbf{y}}_{1}},\cdots ,{{\mathbf{y}}_{C}} \right]}^{T}}$$$ the under-sampled k-space data formed in same rule; $$${{\mathbf{F}}_{\mathbf{U}}}=diag\left( {{\mathbf{U}}_{1}}\mathbf{F},\cdots ,{{\mathbf{U}}_{C}}\mathbf{F} \right)$$$ the operator that performs Fourier transform and then under sampling on each image.
By constraining the joint sparsity of multi-contrast images with $$${{l}_{2,1}}$$$-norm, the multi-contrast images joint reconstruction optimization function can be formulated as: $$\underset{\mathbf{x}}{\mathop{\min }}\,{{\left\| \mathbf{G\Psi x} \right\|}_{2,1}}\ \ \ s.t.\ \ \ \left\| {{\mathbf{F}}_{\mathbf{U}}}\mathbf{x}-\mathbf{y} \right\|_{2}^{2}\le {{\sigma }^{2}}$$, where $$$\mathbf{\Psi }=diag\left( {{\mathbf{\Psi }}_{g}},\cdots ,{{\mathbf{\Psi }}_{g}} \right)$$$, and $$${{\mathbf{\Psi }}_{g}}$$$ denotes graph-based wavelets transform [4] performed on each image, accordingly, $$$\boldsymbol{\alpha}={{\mathbf{\Psi }}_{g}}\mathbf{x}$$$ denotes the coefficients; $$$\mathbf{G}$$$ denotes the grouping operator satisfying $$$\mathbf{G}\boldsymbol {\alpha }=\left[ \begin{matrix} {{\alpha }_{11}} & \cdots & {{\alpha }_{1C}} \\ \vdots & \ddots & \vdots \\ {{\alpha }_{N1}} & \cdots & {{\alpha }_{NC}} \\ \end{matrix} \right]$$$, where the column of $$$\mathbf{G\alpha }$$$ denotes transformation coefficients of one contrast image. Therefore, the $$${{l}_{2,1}}$$$-norm of $$$\mathbf{G}\boldsymbol {\alpha }$$$ can be defined as $$${{\left\|\mathbf{G}\boldsymbol{\alpha} \right\|}_{2,1}}=\sum\limits_{i=1}^{N}{{{\left( \sum\limits_{j=1}^{T}{{{\left| {{\boldsymbol{\alpha}}_{ij}} \right|}^{2}}} \right)}^{{1}/{2}\;}}}$$$. We name the proposed method as joint GBRWT (JGBRWT) reconstruction.
Results
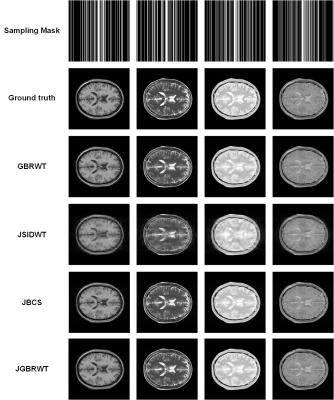
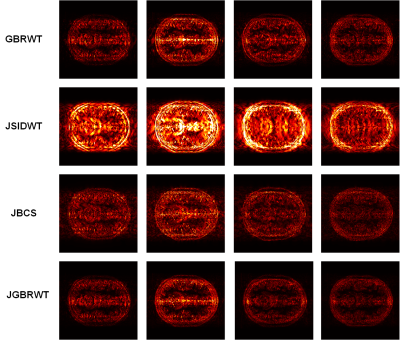
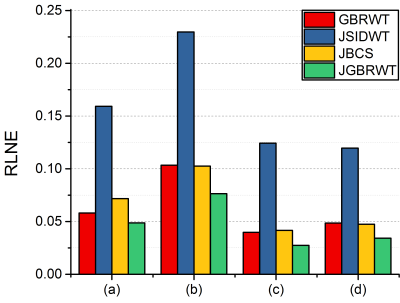
The multi-contrast MRI images obtained from BrainWeb5 are adopted to validate our proposed method. Each contrast image is under sampled with different Gaussian Cartesian sampling pattern (Fig. 1) at the same acceleration factor. The proposed method is compared with three state-of-the-art compressed sensing MRI reconstruction methods: (a) Graph-Based Redundant Wavelet Transform (GBRWT) designed for single contrast image reconstruction4; (b) Joint Shift Invariant Discrete Wavelet Transform (JSIDWT), which is a variant method of proposed method by substituting the sparse transform with SIDWT2, 3 rather than GBRWT; (c) Joint Bayesian Compressed Sensing (JBCS) 6, by which method different contrasts are reconstructed jointly. The relative $$${{l}_{2}}$$$-norm error (RLNE) defined as: $$$\text{RLNE}=\frac{{{\left\| \mathbf{x}-\mathbf{\hat{x}} \right\|}_{2}}}{{{\left\| \mathbf{x} \right\|}_{2}}}$$$, is estimated as a measure of the difference between the fully sampled image $$$\mathbf{x}$$$ and reconstructed image $$$\mathbf{\hat{x}}$$$. The reconstructed images in Fig.1, error images in Fig. 2 and RLNE in Fig. 3 show that: (a) the proposed JGBRWT achieves lower reconstruction errors, implying that joint sparse reconstruction can improve the images than use GBRWT4 to sparsify each image individually. (b) the JGBRWT outperforms the JSIDWT and the state-of-the-art JBCS in terms of lower reconstructed image errors, indicating that more structured image information are preserved by the new approach.Conclusion
We proposed an approach to jointly reconstruct multi-contrast images by taking advantage of the sparsity of multi-contrast images under graph-based wavelets representation. Results show that joint sparse reconstruction achieve lower error than that of single-contrast image sparse reconstruction, and our proposed method outperforms the compared joint reconstruction methods. The proposed approach would be meaningful to accelerate multi-contrast MRI.Acknowledgements
This work was partially supported by National Key R&D Program of China (2017YFC0108703), National Natural Science Foundation of China (61571380, 61302174 and U1632274), Fundamental Research Funds for the Central Universities (20720150109) and Natural Science Foundation of Fujian Province of China (2016J05205). The correspondence should be sent to Dr. Xiaobo Qu (Email: quxiaobo@xmu.edu.cn)References
1. M. Lustig, D. Donoho, and J. M. Pauly, "Sparse MRI: The application of compressed sensing for rapid MR imaging," Magnetic Resonance in Medicine, vol. 58, pp. 1182-1195, 2007.
2. X. Qu, D. Guo, B. Ning, Y. Hou, Y. Lin, S. Cai, and Z. Chen, "Undersampled MRI reconstruction with patch-based directional wavelets," Magnetic Resonance Imaging, vol. 30, pp. 964-977, 2012.
3. X. Qu, Y. Hou, F. Lam, D. Guo, J. Zhong, and Z. Chen, "Magnetic resonance image reconstruction from undersampled measurements using a patch-based nonlocal operator," Medical Image Analysis, vol. 18, pp. 843-856, 2014.
4. Z. Lai, X. Qu, Y. Liu, D. Guo, J. Ye, Z. Zhan, and Z. Chen, "Image reconstruction of compressed sensing MRI using graph-based redundant wavelet transform," Medical Image Analysis, vol. 27, pp. 93-104, 2016.
5. C. A. Cocosco, V. Kollokian, Kwan, and A. C. Evans, "BrainWeb: Online interface to a 3D MRI simulated brain database," Neuroimage, vol. 5, pp. 425, 1997.
6. B. Bilgic, V. K. Goyal, and E. Adalsteinsson, "Multi-contrast reconstruction with Bayesian compressed sensing," Magnetic Resonance in Medicine, vol. 66, pp. 1601-1615, 2011.
Figures