3526
Sparsely Sampled Cardiac Diffusion Tensor Imaging Using Phase-Corrected Joint Low-Rank and Sparsity Constraints1Department of Bioengineering, University of California, Los Angeles, Los Angeles, CA, United States, 2Biomedical Imaging Research Institute, Cedars-Sinai Medical Center, Los Angeles, CA, United States, 3Cardiovascular Research Center, Massachusetts General Hospital and Harvard Medical School, Charlestown, MA, United States, 4Severance Cardiovascular Hospital, Seoul, Republic of Korea, 5Yonsei-Cedars-Sinai Integrative Cardiovascular Imaging Research Center, Yonsei University, Seoul, Republic of Korea, 6College of Medicine, Yonsei University, Seoul, Republic of Korea
Synopsis
We propose to sparsely sample in vivo cardiac diffusion tensor imaging (CDTI) by combining a phase-corrected low-rank model and sparsity constraint. The proposed method was evaluated on 7 hypertrophic cardiomyopathy patients. Helix angle and mean diffusivity maps were compared against employing single constraint, and changes in helix angle transmurality and mean diffusivity were evaluated using Wilcoxon signed rank test to statistically determine the highest achievable acceleration factors preserving CDTI measurements with no significant difference. Our framework shows promise in accelerating acquisition window while preserving myofiber architecture features, and may allow higher spatial resolution or shorter temporal footprint in the future.
Introduction
Cardiac diffusion tensor imaging (CDTI) is a non-contrast, non-invasive technique capable of assessing the anatomic microarchitecture of the myocardium1. However, in vivo CDTI is difficult due to substantial acquisition requirements2. Recently compressed sensing (CS) has shown great promise in accelerating CDTI with highly undersampled k-space3,4. Another promising approach is low-rank (LR) modeling which has been used to accelerate CDTI and brain DTI5-7. Our work employs a joint framework to sparsely sample in vivo CDTI by combining low-rank and spatial sparsity constraints, combined with a phase correction procedure to enhance the low-rankness. We demonstrate the superior performance of the proposed method, reaching higher acceleration factor and significantly improving the accuracy of CDTI-based measurements.Methods
Due to the strong correlation between free-breathing, diffusion-weighted images along different diffusion directions, we leverage the low-rank structure of diffusion-weighted images $$$\textbf{X}\in\mathbb{C}^{M\times N}$$$ using a partially separable model8. This model is particularly useful when a phase map $$$\textbf{P}\in\mathbb{C}^{M\times N}$$$ is applied to compensate for the drastic phase inconsistency across diffusion directions7, i.e., $$$\textbf{X}=\textbf{P}\circ(\textbf{U}\textbf{V})$$$, where $$$M$$$ represents the number of voxels, $$$\textbf{V}\in\mathbb{C}^{L\times N}$$$ contains “temporal” basis functions (containing contributions from diffusion and respiratory motion), and $$$\textbf{U}\in\mathbb{C}^{M\times L}$$$ contains spatial coefficients with $$$L\lt \min\{M,N\}$$$. We also include a group sparsity constraint to leverage the CS framework. We propose to reconstruct $$$\textbf{X}$$$ in three steps:
1) Estimate phase map: We propose to estimate $$$\textbf{X}$$$ from an intermediate solution of employing only a sparsity constraint:
$$\widetilde{\textbf{X}}=\arg\min_{\textbf{X}}||\textbf{d}-E(\textbf{X})||_2^{2}+\lambda \text{R}_{s}(\textbf{X})\quad\quad\quad\quad\quad\quad\quad (1)$$
with $$$P_{jk}=\exp{(i\angle\widetilde{X}_{jk})}$$$, where $$$\textbf{d}$$$ denotes undersampled k-space data, $$$E(\cdot)$$$ performs spatial encoding and sparse sampling, $$$\lambda$$$ represents the regularization factor, and $$$\text{R}_{s}(\cdot)$$$ is the regularization penalty promoting group sparsity.
2) Estimate "temporal" subspace: We propose to estimate $$$\textbf{V}$$$ from the SVD of the magnitude image $$$|\widetilde{\textbf{X}}|$$$ by collecting $$$L$$$ most significant right singular vectors.
3) Recover spatial coefficients: Lastly, we recover the spatial coefficient matrix by
$$\textbf{U}=\arg\min_{\textbf{U}}||\textbf{d}-E(\textbf{P}\circ(\textbf{U}\textbf{V}))||_2^{2}+\lambda \text{R}_{s}(\textbf{UV}).\quad\quad\quad\quad\quad\quad\quad (2)$$
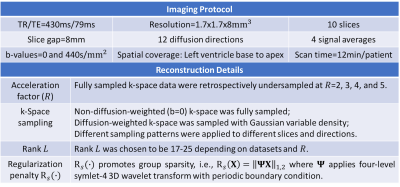
Data were acquired from $$$n$$$=7 hypertrophic cardiomyopathy (HCM) patients. Diffusion MRI was performed on a 3T Siemens Prisma scanner. A second-order motion-compensated diffusion tensor sequence2 was used replacing the bSSFP readout with a single-shot EPI readout. Imaging protocol and reconstruction details are displayed in Table 1. The diffusion tensor, along with helix angle (HA) and mean diffusivity (MD), was log linearly-fitted after standard mutual information affine registration. Helix angle transmurality (HAT) was calculated by radially sampling the HA along 60 transmural directions and linearly fitting between HA and transmural depth. Both global (7 samples) and regional (16 AHA segments/subject × 7 subjects = 112 samples) HAT and MD of the entire group were compared between fully-sampled (reference) and reconstructed data at varying acceleration factors (R) using a Wilcoxon signed rank test with Bonferroni correction.
Results
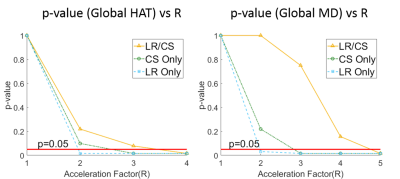
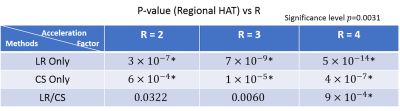
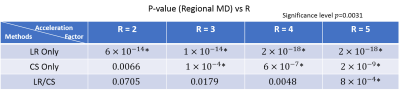
Fig. 1 shows a comparison between the proposed method (LR/CS) and employing either low-rank (LR Only) or sparsity constraint alone (CS Only). LR/CS shows superior performance in removing image artifacts, thus reducing errors and preserving more accurate HA and MD features across the myocardium. Fig. 2 shows the comparison of p-values, derived from global HAT and MD, over R using LR/CS, LR Only and CS Only. LR/CS can reach higher acceleration (R=3 for HAT, R=4 for MD) without significantly differing (p>0.05) from the reference, than is possible with LR Only (R<2 for HAT and MD) and CS Only (R=2 for HAT, R=3 for MD). Tables 2 and 3 show the comparison of p-values, derived from regional HAT and MD, over R. LR/CS shows consistency with global analysis, preserving regional HAT (R=3) and MD (R=4) across the entire group without significant difference (p>0.0031) from the reference, which outperforms LR Only (p>0.0031 constantly for HAT and MD) and CS Only (p<0.0031 constantly for HAT, R=2 for MD).Discussion
The combination of LR and CS outperforms either LR or CS alone in removing image artifacts and preserving more accurate image features. In addition, LR/CS allows higher acceleration (R=3 for HAT, R=4 for MD), preserving both global and regional HAT and MD measurements without significant difference from the reference, than using either constraint alone.Conclusion
We propose to sparsely sample in vivo cardiac diffusion tensor imaging by combining a phase-corrected low-rank model and spatial sparsity constraint. Population-based statistical analysis reveals that an acceleration factor of 3 can be achieved, reducing the temporal footprint of the readout 3-fold or potentially increasing spatial resolution by 3-fold given the same temporal footprint, while improving image quality and producing no significant difference of helix angle transmurality and mean diffusivity measurements. The proposed method can potentially be applied to reduce scan time by shortening the number of diffusion directions or signal averages.Acknowledgements
This work was supported by NIH 1R01HL124649, NIH R21EB024701-01, and NIH T32HL116273.References
1. Mekkaoui C, Reese TG, Jackowski MP, Bhat H, Sosnovik DE. Diffusion MRI in the heart. NMR Biomed 2017;30(3).
2. Nguyen C, Fan Z, Xie Y, Pang J, Speier P, Bi X, Kobashigawa J, Li D. In vivo diffusion-tensor MRI of the human heart on a 3 tesla clinical scanner: An optimized second order (M2) motion compensated diffusion-preparation approach. Magn Reson Med 2016;76(5):1354-1363.
3. Wu Y, Zhu YJ, Tang QY, Zou C, Liu W, Dai RB, Liu X, Wu EX, Ying L, Liang D. Accelerated MR diffusion tensor imaging using distributed compressed sensing. Magn Reson Med 2014;71(2):763-772.
4. McClymont D, Teh I, Whittington HJ, Grau V, Schneider JE. Prospective acceleration of diffusion tensor imaging with compressed sensing using adaptive dictionaries. Magn Reson Med 2016;76(1):248-258.
5. Ma S, Nguyen C, Christodoulou A, Luthringer D, Kobashigawa J, Li D. Accelerated Cardiac Diffusion Tensor Imaging Using Joint Low-Rank and Sparsity Constraint. In Proceedings of the 25th Annual Meeting of ISMRM, Honolulu, Hawaii, USA, 2017. Abstract 6603.
6. Huang J, Wang L, Chu C, Zhang Y, Liu W, Zhu Y. Cardiac diffusion tensor imaging based on compressed sensing using joint sparsity and low-rank approximation. Technology and Health Care 2016;24(s2):S593-S599.
7. Gao H, Li L, Zhang K, Zhou W, Hu X. PCLR: phase-constrained low-rank model for compressive diffusion-weighted MRI. Magn Reson Med 2014;72(5):1330-1341.
8. Liang Z-P. Spatiotemporal imaging with partially separable functions. IEEE ISBI, 2007: 988-991.
Figures