3523

A Python-based MRI Reconstruction Toolbox, “MRIPY”, for Compressed Sensing, Parallel Imaging and Machine Learning
Peng Cao1, Xucheng Zhu1, Jing Liu1, Yan Wang1, and Peder Larson1

1Department of Radiology and Biomedical Imaging, University of California at San Francisco, San Francisco, CA, United States

Synopsis

A python-based open-source package, “MRIPY” combines the existing MRI reconstruction methods, i.e. compressed sensing and parallel imaging, with deep neural networks that are implemented in the Tensorflow software.

Purpose

The purpose of this research project is to develop and validate an open-source toolbox for next-generation accelerated MRI reconstruction. This abstract presents a python-based open-source package as the output of this project, developed to combine the existing MRI reconstruction methods, i.e. compressed sensing and parallel imaging, with deep neural networks that can be integrated with software such as Tensorflow and PyTorch.

Methods

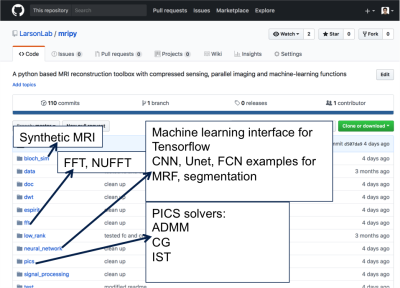
Fig. 1 shows a few key functions of this python package (https://github.com/LarsonLab/mripy/):

  • MRI reconstruction with compressed sensing 1 via convex optimization algorithms: gradient descent, nonlinear conjugate gradient and alternating direction method of multipliers 2,3
  • Parallel imaging, ESPiRIT 4, which is a Hankel low rank and PCA based analysis method in combination with compressed sensing reconstruction 4
  • Interface with Tensorflow (https://www.tensorflow.org) for training and testing neural networks in classes/functions that can be easily utilized in the abovementioned optimization algorithms during MRI reconstruction/processing
  • FFTW (https://hgomersall.github.io/pyFFTW/) /cuFFT (https://developer.nvidia.com/cufft) /DWT (https://pywavelets.readthedocs.io/en/latest/) interfaces, and custom-built 1D/2D/3D non-uniform FFT 5 with optional GPU acceleration capabilities (implemented in CUDA and numba)
  • Numerical MRI signal simulation with optional GPU acceleration capabilities (implemented in CUDA and numba)

Results

Figures 2-5 show sample outputs generated from MRIPY, including a range of MRI reconstruction methods as well as integration with deep neural networks:

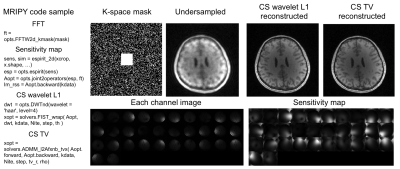
Fig. 2 shows an example of parallel imaging and compressed sensing reconstruction with alternating direction method of multipliers (ADMM) and wavelet L1 or total variation minimization regularization. Raw MRI data was from website (http://people.eecs.berkeley.edu/~mlustig/CS.html).

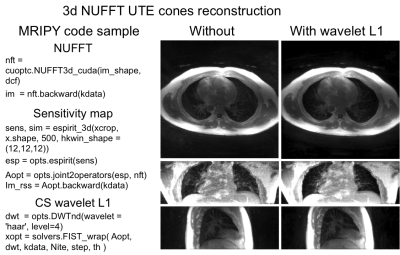
Fig. 3 shows NUFFT based reconstruction for UTE images (after MIP) acquired using a 3D UTE Cones sequence.

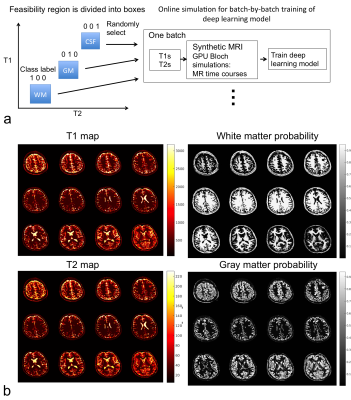
Fig. 4 shows whole brain segmentation/relaxometry as the direct output of a deep neural network trained with the synthetic MRI data. The in vivo brain MRI data was from Dr. Jing Liu.

Fig. 5 shows another more complex task that is the detection/segmentation of myocardium from MRI image. A fully convolutional network performed the segmentation as an example provide in MRIPY. The MRI data was from Dr. Yan Wang.

Conclusion

The new reconstruction and neural network segmentation methods developed will provide improved precise measurements in MRI.

Acknowledgements

We receive grant support (NIH R21NS089004 and NIH R56HL133663 ) from NIH.

References

1. Lustig, M. & Pauly, J. M. SPIRiT: Iterative self-consistent parallel imaging reconstruction from arbitrary k-space. Magn. Reson. Med. 64, 457–471 (2010).

2. Afonso, M. V., Bioucas-Dias, J. M. & Figueiredo, M. A. T. An augmented lagrangian approach to the constrained optimization formulation of imaging inverse problems. IEEE Trans. Image Process. 20, 681–695 (2011).

3. Boyd, S., Parikh, N., E Chu, B. P. & Eckstein, J. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Found. Trends Mach. Learn. 3, 1–122 (2011).

4. Uecker, M. et al. ESPIRiT — An Eigenvalue Approach to Autocalibrating Parallel MRI : Where SENSE Meets GRAPPA. 0, 1–12 (2013).

5. Greengard, L. & Lee, J. Accelerating the Nonuniform Fast Fourier Transform ∗. 46, 443–454 (2004).

Figures

Figure 1 MRIPY toolbox contains three major blocks: synthetic MRI, iterative/non-iterative reconstructions (PICS, ESPIRiT, IDEAL), and machine learning interface.

Figure 2 An example of parallel imaging (PI) and compressed sensing (CS) reconstruction (PICS) with alterative direction multiplier method (ADMM) and wavelet L1 or total variation minimization (TV) regularization, using the MRIPY toolbox. Raw MRI data is from website (http://people.eecs.berkeley.edu/~mlustig/CS.html). MRIPY code sample shows the PICS reconstruction can be implemented in a few lines in python.

Figure 3 Example of 3d NUFFT based reconstruction for UTE cones image (after MIP) without and with wavelet L1 regularization using the MRIPY toolbox. Code sample shows the each step in the reconstruction can be implemented by calling one function/class in this toolbox.

Figure 4 (a) Proposed method assumed the feasible parameter space can be divided into boxes that were binary labeled for white matter (WM), gray matter (GM), and cerebrospinal fluid (CSF). A deep neural network with 6 fully connected layers was used to perform pixel-wise estimation of T1, T2, and WM, GM and CSF probabilities. The neural network was trained with T1 and T2 drawn from the parameter feasibility region (in Fig. a). (b) Whole brain segmentation/relaxometry in vivo were the direct output of neural network trained with the synthetic MRI in Fig. a. The MRI data was from Dr. Jing Liu.

Figure 5 (a) Illustration of neural network and MRIPY code sample, each layer was implemented by one line in python. (b) Detection/segmentation of myocardium from MRI image. A fully convolutional network performed the segmentation as an example provide in MRIPY. The MRI data was from Dr. Yan Wang.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
3523