Synopsis

Partial Fourier MRI (PF-MRI) is a common fast MRI technique to reduce the scan time. While POCS PF-MRI is known to produce MRI images with least amount of RMSE error, homodyne PF-MRI is popularly used in clinical practice. In this abstract we did digital phantom experiments to show that for smoothly varying phase, such as for FSE, POCS localises the error while an over-/under-estimation in image intensity is observed for Homodyne PF-MRI technique. However for fast varying phase such as for GRE, error is localised for Homodyne compared to POCS PF-MRI technique.

Introduction

Method

Two digital MRI phantoms were generated and analysed using MATLAB (Mathworks, Natick, MA) to mimic the source of phase present in the MRI image and performance of homodyne and POCS PF-MRI techniques.

1) Hardware imperfection Phantom: This phantom simulates the phase changes due to the hardware imperfections such as, B₀ inhomogeneity and gradient coil inhomogeneity by varying the phase smoothly over the image. A 512×512 image was generated with unit magnitude. Fig. 1 shows the phase of the image. In our experiments, PF sampling was applied along the vertical direction of the image; each vertical line in the MRI image is reconstructed independently. Therefore, phase was varied linearly along vertical direction from centre to the edge of the image from a constant phase of π/2 over the 10 pixels in the middle of the image. The rate at which phase is varying linearly is decreased along horizontal direction to mimic the range of slowly varying phase over the image. Such phase variation is expected in fast spin echo (FSE) acquired MRI images.

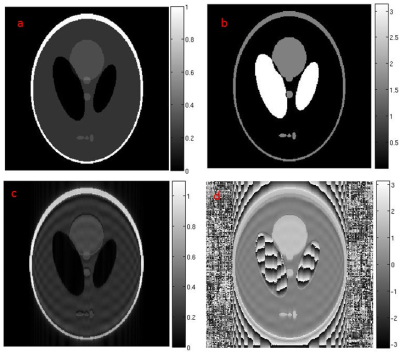
2) Tissue Type Phantom: This phantom simulates the sudden change in phase due to the changes in tissue type such as water-fat and susceptibility. Shepp-Logan phantom was used with modified phase of different parts (ellipses of the phantom) of the image as shown in Fig.2. All the ellipses inside the phantom and the annular boundary of the phantom was assigned a phase of π/2. The phase variations in the phantom mimic the sudden phase variations across tissue types. Such phase variation is expected in GRE and EPI acquired MRI images.

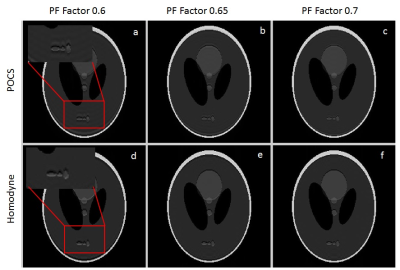
Quantitative assessment of the homodyne and POCS PF-MRI technique is done for different PF factor (56.25% to 93.75% in steps of 6.25%) using RMSE between reconstructed images and ground truth image.

Results and Discussion

POCS technique consistently performed better than homodyne technique in quantitative assessment for the whole range of PF factor (Fig.3) for both the phantoms. Compared to tissue type phantom, sharp rise in error is observed for homodyne technique at lower acceleration factor for hardware imperfection phantom. This suggests that higher PF-factor can be used when POCS PF-MRI technique is used for MRI images acquired using FSE data acquisition.

Qualitative assessment of the hardware imperfection phantom shows that for POCS PF-MRI technique error is present only at the interface of phase transition while a consistent under-/over-estimation in magnitude over the whole phase varying regions was observed for homodyne PF-MRI technique Fig.4. This under-/over-estimated image intensity can lead to false diagnosis in clinical practice.

Qualitative assessment of the tissue type phantom shows difference in distribution of error from the interfaces with fast transition in phase Fig 5. The error in POCS PF-MRI technique was distributed over the space while it was localized for homodyne PF-MRI technique. The spread of error in POCS PF-MRI reconstructed images may occlude or affect the diagnosis of the structures neighbouring the regions with sharp transition in phase.

Conclusion

Acknowledgements

References

1. Noll, Douglas C. et al. Conjugate phase MRI reconstruction with spatially variant sample density correction. IEEE transactions on medical imaging 24 3 (2005): 325-36.

2. Haacke, E. M., E. D. Lindskogj, and W. Lin. A fast, iterative, partial-Fourier technique capable of local phase recovery. Journal of Magnetic Resonance (1969) 92.1 (1991): 126-145.

3. Chen, Ying, et al. Partial Fourier transform reconstruction for single‐shot MRI with linear frequency‐swept excitation. Magnetic resonance in medicine 69.5 (2013): 1326-1336.

4. Liang, Zhi-Pei, and Paul C. Lauterbur. Principles of magnetic resonance imaging: a signal processing perspective. SPIE Optical Engineering Press, 2000.

5. McGibney G, Smith MR, Nichols ST, Crawley A. Quantitative evaluation of several partial Fourier reconstruction algorithms used in MRI. Magn Reson Med 1993; 30:51-59