3518
Optimization-Based Simultaneous Combination and Unwrapping for MR Phase Imaging1Imaging Research Laboratories, Robarts Research Institute, London, ON, Canada, 2Graduate Program in Biomedical Engineering, Western University, London, ON, Canada, 3Medical Biophysics, Western University, London, ON, Canada
Synopsis
MRI phase allows for the extraction of inherent tissue contrasts arising from differences in magnetic susceptibility. However, in order to enhance signal-to-noise ratio and accelerate acquisition, modern MRI uses multiple receiver coils. Extracting susceptibility information relies on combining phase information from these multiple channels. Once combined, phase unwrapping beyond the [$$$-\pi$$$, $$$\pi$$$] range allows for further processing and visualization. These processes can be sensitive to noise and errors which are compounded during serial processing, motivating more robust integrated algorithms. This paper introduces simultaneous combination and unwrapping (SCAU) that simultaneously estimates channel phase offset images and a combined unwrapped image.
INTRODUCTION
Magnetic susceptibility of tissue can be measured using phase sensitive MRI. The extraction of this information is often achieved by processing phase images, obtained from several MR receive coils (channels). 1 Each single-channel phase image can be represented as the sum of a channel-specific phase offset image and a shared unwrappable phase image; the latter is estimated through channel combination and subsequent unwrapping. This process has two shortcomings; (1) noise in the individual channels can lead to difficulty in channel combination, especially in the presence of phase poles, and (2) error introduced in channel combination can have a detrimental effect on unwrapping algorithms and further processing steps. The emerging clinical utility of MR phase imaging has motivated further development of phase-sensitive channel combination approaches. In this work, we present an optimization-based algorithm that simultaneously performs channel combination and phase unwrapping, using an underlying Gaussian noise model in the complex image. This algorithm operates directly on the phase information, using a cyclic manifold to represent the individual smooth phase offset images for each channel.THEORY and METHODS
Optimization: Simultaneous Combination And Unwrapping (SCAU) optimizes the functional:
$$\underset{\theta_c(x),\theta_U(x)}{\min}\int_{\Omega}\left( -\sum^{n}_{c=1}\ln P \left( \theta_c^{(obs)}(x) -\theta_c(x) - \theta_U(x)|M_c^{(obs)}(x)\right) + \alpha \sum_{c=1}^{n} |\nabla \theta_c(x)|^2 + \beta |\nabla \theta_U(x)| \right) dx$$
where $$$\theta_c^{(obs)}(x)$$$ and $$$M_c^{(obs)}(x)$$$ are the magnitude and phase of the $$$c$$$th channel image respectively, $$$\theta_c(x)$$$ is the estimated phase offset image for the $$$c$$$th channel and $$$\theta_U(x)$$$ is the estimated unwrapped phase image. In this framework, $$$\theta_c^{(obs)}(x)$$$, $$$\theta_c(x)$$$, and $$$\theta_c^{(obs)}(x)-\theta_c(x)-\theta_U(x)$$$ are all treated as existing over a cyclic manifold2 which allows for the natural handling of smooth images containing phase poles decoupled from the corresponding magnitude image whereas is treated as existing over a more traditional Euclidean manifold with range extending arbitrary beyond [$$$-\pi$$$,$$$-\pi$$$]. The probability equation $$$P(\theta|M)$$$ is the probability density of a positive real number $$$M$$$ plus a random circularly symmetric Gaussian variable having an overall phase of $$$\theta$$$. This functional is addressed through augmented Lagrangian multipliers whose descent steps preserve both the wrapped nature of $$$\theta_c(x)$$$ and the unwrapped nature of $$$\theta_U(x)$$$ thus unwrapping the phase in conjunction with smoothing the individual channel phase images to recovering the channel phase offset images.
Phantom Study: A digital phantom study was constructed to evaluate the efficacy of SCAU in comparison to a decoupled approach featuring channel combination3 followed by phase unwrapping.4 The phantom consisted of four bell-shaped phase curves of height $$$\pm 2\pi$$$ and two $$$1$$$px wide lines of intensity $$$\pm 0.125\pi$$$. The bell-shaped curves were designed to evaluate how well the algorithms can unwrap large phase variations and the thin lines evaluate how well it retains small structures. Sixteen phantom channels (three of which are shown in Figure 1) with differently oriented sensitivity patterns, smoothly varying phase offsets and phase pole locations where created and then polluted with independent and identically distributed, circularly-symmetric Gaussian noise at an SNR of 10.
Imaging: Healthy volunteers were imaged at 7T (Agilent Technologies, Santa Clara, USA) using a 16-channel head coil. Three-dimensional whole-brain multi-echo gradient echo images were acquired (6 echoes, TR/TE/Echo spacing: 40/3.77/4.1 ms, matrix: 380x340x102, FOV: 190x170x127.5 mm). The channel data were saved for later processing.
RESULTS and DISCUSSION
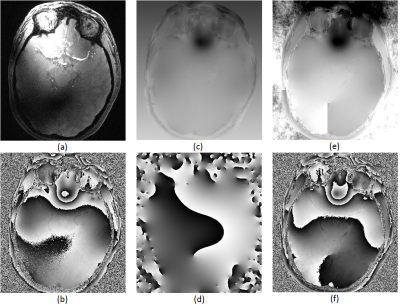
This work presents the development of an optimization-based algorithm for simultaneous channel combination and phase unwrapping. The results from the phantom experiment indicate that SCAU is capable of de-noising the combined phase image while preserving small-structures and being less sensitive to noise than the comparative method. Arrows in Figure 2 d) and e) indicate where excessive noise had led the comparative method to introduce an artefactual phase wrap into the channel-combined image, complicating unwrapping. On the other hand, the SCAU approach results in the mitigation of these artefacts through heavy penalization. In vivo results (Figure 3) demonstrate that these capabilities can readily translate to clinical neurological applications. The run-time for our MATLAB implementation of SCAU on this image is 359 s compared to a cumulative run-time of 18 s for the comparative method. Being inherently parallelizable, we expect to significantly decrease running time in future GPU-accelerated implementations.CONCLUSION
By performing phase unwrapping in conjunction with channel combination, this work presents an algorithm that mitigates erroneous phase wrapping artefacts even in the presence of phase wraps in low SNR individual channel images. This algorithm minimizes the error in phantom experiments via de-noising in comparison to the decoupled approach while also preserving thin, low-intensity structures. The preservation of these structures enhances SCAU's ability to visualize veins and other minute anatomy whose contrast results from differing magnetic tissue susceptibility.Acknowledgements
John S.H. Baxter is supported by the Natural Sciences and Engineering Research Council of Canada through the Canadian Graduate Scholarship program. Zahra Hosseini is supported by the Ontario Graduate Scholarship. Financial Assistance was provided by: The Canadian Foundation for Innovation, # 20994, The Natural Sciences and Engineering Council of Canada, # RPGIN 2014-04504, and The Canadian Institutes for Health Research, # FDN 143232.References
[1] Haacke, E. M., Xu, Y., Cheng, Y.C.N., & Reichenbach, J. R. Susceptibility Weighted Imaging (SWI), Magn. Res. Med., 2004, 52:612-618.
[2] Baxter, J.S.H., Hosseini, Z., Peters, T.M., & Drangova, M. Cyclic Continuous Max-Flow: A Third Paradigm in Generating Local Phase Shift Maps in MRI, IEEE Trans. on Medical Imaging, 2017, PP(99): 1-13.
[3] Walsh DO, Gmitro AF, Marcellin MW. Adaptive reconstruction of phased array MR imagery, Magn. Res. Med., 2000, 43:682-690.
[4] Bioucas-Dias, J. M., & Valadao, G. Phase unwrapping via graph cuts. IEEE Trans. on Image Processing, 2007, 16(3):698-709.
Figures