3514

Reduced-FOV k-space Variant Radial Parallel Imaging Reconstruction for Real-time Cardiac MR
Yu Yulee Li1,2, Shams Rashid1, Yang Cheng1, William Schapiro1, Kathleen Gliganic1, Ann-Marie Yamashita1, Marie Grgas1, Michelle Maragh1, and Jie Jane Cao1,3

1Cardiac Imaging, St. Francis Hospital DeMatteis Center for Cardiac Research and Education, Greenville, NY, United States, 2Radiology, Stony Brook University (SUNY), Stony Brook, NY, United States, 3Medicine, Stony Brook University (SUNY), Stony Brook, NY, United States

Synopsis

Radial imaging is k-space variant, but mostly uses k-space invariant methods in image reconstruction. This permits reconstructing images with lower computation complexity at a cost of performance. Here a k-space variant parallel imaging reconstruction technique is developed to reconstruct Cartesian data directly from multi-channel radial samples with affordable computation. It is demonstrated that this technique offers the ability to collect real-time images with a temporal resolution of 40ms and a spatial resolution of 1.7mm. The new technique outperforms those gridding-based methods with k-space invariant algorithms in a stress cardiac test.

Introduction

Radial imaging may benefit cardiac MRI with its low motion sensitivity and high sampling efficiency. However, radial sampling is k-space variant, making it challenging to reconstruct images with parallel imaging. Most existing techniques trade performance for lower computation complexity using k-space invariant methods, providing a sub-optimal solution to image reconstruction. This work introduces a k-space variant parallel imaging reconstruction technique that can optimize radial imaging performance with an affordable computation cost. The presented technique uses radial samples to estimate multi-channel correlation functions which are in turn used to calculate k-space variant parallel imaging relationship between Cartesian and radial samples. Cartesian data may be generated directly from the linear combination of its neighboring multi-channel radial samples. It is found that k-space variant reconstruction can improve radial imaging performance. In addition, the new technique may reconstruct images with a reduced field of view (FOV) for less computation time. It is demonstrated that high-quality images may be generated from16 radial lines, providing an approach to free-breathing real-time imaging with a temporal resolution of 40ms and a spatial resolution of 1.7mm during a stress cardiac test.

Methods

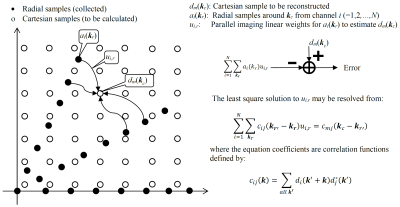
A previously-developed framework of correlation imaging1-3 is used to convert radial parallel imaging reconstruction into the estimation of correlation functions. As shown in Figure 1, every Cartesian datum, dm(kc), may be calculated from its neighboring multi-channel radial samples, {ai(kr), i=1,2…,N}, with parallel imaging in a point-wise fashion. The parallel imaging relationship (linear weights ui,r) for every datum can be resolved from a set of linear equations with the coefficients equal to correlation functions on the non-Cartesian grid (kr' -kr and kc-kr'). These correlation functions may be estimated from radial samples based on Nyquist theorem4 as illustrated in Figure 2. This method first estimates low-resolution Cartesian correlation functions from central k-space Cartesian data generated by radial samples. As these functions meet the Nyquist criterion, they may be further used to generate correlation functions at an arbitrary k-space position with Whittaker-Shannon interpolation5.

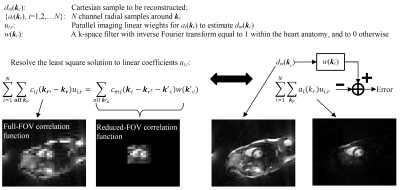
To implement k-space variant reconstruction with commonly-available computer hardware, the correlation imaging model in Figure 1 is modified by introducing an additional filter w(kc) in Figure 3. This k-space filter suppresses MRI signals from the outside of heart anatomy, making it possible to reconstruct images within a small FOV. By reducing the FOV, Cartesian k-space data may be undersampled without any loss. This allows for the calculation of only a subset of the full Cartesian k-space data, making it possible to reconstruct images with an affordable computation cost.

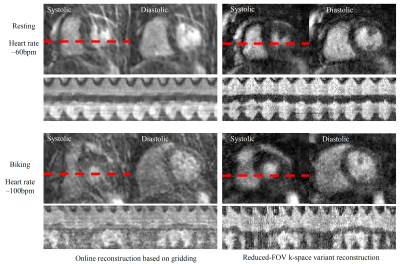
For feasibility demonstration, cardiac imaging experiments were performed with a balanced steady-state free-precession sequence. To investigate reconstruction in simulation studies, a full k-space single-phase radial dataset was collected with breath-holding (segmented, FOV 300mm, 128 views, 1.2mm spatial resolution, TR/TE 4.6/2.3ms, flip angle 65°). The new technique was demonstrated in a stress (biking) cardiac test. In this test, the subject was first scanned when resting with a heart rate of ~60bpm and then when biking with a heart rate of ~100bpm. Real-time cardiac images were collected with free-breathing (FOV 300mm, 220 time frames, 16 views per time frame, 1.7 mm spatial resolution, TR/TE 2.5/1.3ms, flip angle 50°). The results were compared with online reconstruction provided by the MRI manufacturer.

Results

Figure 4 shows the reconstruction results with different radial lines using the single-phase cardiac data. In reference to gridding, k-space variant reconstruction performs better with a small number of views (≤32). Compared to the full-FOV reconstruction, the reduced-FOV reconstruction gives the same image quality with less computation time, providing a computation cost only ~5 times higher than linear gridding. Figure 5 shows real-time cardiac imaging results. With 16 views, the online reconstruction based on gridding gives significant spiking artifacts and image blurs. In comparison, k-space variant reconstruction does not generate considerable spiking artifacts. The images give good spatial and temporal resolutions during systolic and diastolic phases. It should be noted that imaging speed is critical to stress (biking) test because there exist both rapid heart-beats/respiration and continuous body movement. In this case, the gain from k-space variant reconstruction is more significant.

Discussion

The k-space variant parallel imaging linear weights (Figure 1) are the combination of non-linear gridding and linear parallel imaging. They also include an additional anti-aliasing filter in reduced-FOV reconstruction (Figure 3). The reduced-FOV k-space variant reconstruction is suitable for cardiac imaging where the region of interest is small (within the heart anatomy). This technique can considerably improve radial imaging performance with an affordable computation cost.

Conclusion

Radial imaging performance may be improved using k-space variant parallel imaging reconstruction with an affordable computation cost.

Acknowledgements

This work is supported by NIH R01EB022405.

References

1. Li, Y et al., MRM 2012, 68:2005-2017.

2. Li, Y et al., MRM 2015, 74(6): 1574-1586.

3. Li, Y, Proc Intl Soc Mag Reson 2017, 24: 5156.

4. Shannon, C et al., Proc Institute of Radio Engineers 1949, 37(1): 10-21.

5. Whittaker, T., Proc Royal Soc Edinburgh 1915, 35: 181-194.

Figures

Figure 1. A correlation imaging framework1-3 is used to convert radial parallel imaging reconstruction into the estimate of multi-channel correlation functions. This framework minimizes the least square error between every Cartesian datum at kc and the linear combination of its multi-channel radial neighbors at kr's. The linear weights for reconstruction can be resolved point-wisely from linear equations with the coefficients equal to correlation functions on the non-Cartesian grid (kr' -kr and kc-kr'). If these correlation functions be estimated, Cartesian data can be reconstructed directly from multi-channel radial data in a k-space variant fashion.

Figure 2. Based on Nyquist theorem, radial samples are written as the Whittaker-Shannon interpolation from Cartesian data in the central k-space. This yields a set of linear equations for resolving low-resolution images which are in turn used to estimate correlation functions in Cartesian space. The estimated Cartesian-space correlation functions are further used to estimate correlation functions at an arbitrary k-space position using Whittaker-Shannon interpolation. It should be noted that correlation imaging (Figure 1) requires correlation functions only at low |k| values and an estimate of central k-space correlation functions (low-resolution) is thus sufficient for image reconstruction.

Figure 3. Reduced-FOV reconstruction may be implemented by introducing an additional k-space filter w(kc) in the correlation imaging model illustrated by Figure 1. Correspondingly, the right side of linear equations should be modified with reduced FOV correlation functions generated by passing the original correlation functions through the filter w(kc). The resolved linear weights will lead to the reconstruction of reduced-FOV images (bottom-right).

Figure 4. Comparison of full-FOV and reduced-FOV k-space variant reconstruction methods in reference to gridding. In all the experiments with different view numbers, both two methods perform better than gridding while the reduced-FOV reconstruction needs less computation time. This permits implementing reduced-FOV reconstruction with affordable computation hardware for clinical use.

Figure 5. Real-time radial imaging with reduced-FOV k-space variant reconstruction in reference to that with online gridding-based reconstruction provided by the MRI manufacturer. The real-time data include 16 views in each time frame, providing a spatial resolution of 1.7mm and a temporal resolution of 40ms. The k-space variant reconstruction gives less artifacts and better spatial/temporal resolutions. This gain is more significant in images collected when biking with both rapid heart-beats/respiration and body movements.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
3514