3512
Parallel Imaging Reconstruction Algorithm Mitigating SNR Loss Using Phase Distribution for Fast Spin Echo Sequence1Hitachi, Ltd. Healthcare Business Unit, Tokyo, Japan
Synopsis
Parallel imaging is widely used in clinical routine practice. However, SNR degradation occurs due to undersampling and higher g-factor in higher acceleration factor. In this study, a new algorithm of parallel imaging reconstruction mitigating noise enhancement for fast spin echo sequence was proposed. The algorithm uses information of phase distribution of unaliased image, aliasing image, and folded image. SNR was compared in vivo T2 weighted image between full sampling, conventional parallel imaging, and proposed method. And higher SNR was demonstrated.
Purpose
The purpose of this study is investigating new parallel imaging reconstruction algorithm mitigating SNR loss.Introduction
Fast Spin Echo sequence (FSE) is widely used in clinical routine MRI. To shorten scan time, parallel imaging1-3 is usually applied. However, SNR is degraded due to higher geometry factor of receiving coil and undersampling, therefore high acceleration factor is not used. To mitigate SNR loss, many reconstruction algorithms such as shifting aliasing pattern4 and phase-constrained parallel imaging5 were proposed and the number of channel of receiving coil was increased. In this study, a new parallel imaging reconstruction algorithm was investigated to mitigate SNR loss. The algorithm uses phase distribution of FSE images that can be estimated with high accuracy using information of center of k-space. Error propagation was calculated, and minimized enhancement of noise. Higher SNR was demonstrated in vivo T2 weighted images.Method
Reconstruction Algorithm
i) Calculation of phase distribution
Sampling pattern of proposed algorithm was same as conventional parallel imaging. Central 64 lines of k-space (ACS) was fully sampled to estimate phase distribution. Phase distribution of unaliased image ( $$$\theta^i$$$ ), aliased image ( $$$\phi^i$$$ ), and folded image ( $$$\psi^i$$$ ) were estimated as equation 1 using ACS data. $$\begin{align}\theta^i&=angle(FFT(ACS^i))\\\phi^i&=angle(\frac{FFT(ACS^i_{pi})}{FFT(ACS^i)})\ \ (1)\\\psi^i&=angle(FFT(ACS^i_{pi}))\end{align}$$ Where i is index of receiver channel, FFT is Fourier transformation, $$$ACS^i$$$ is central 64 lines of k-space of channel i, and $$$ACS^i_{pi}$$$ is under sampled data of $$$ACS^i$$$.
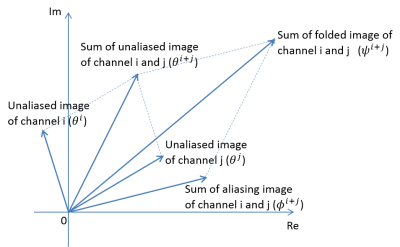
ii) Unfolding algorithm
Figure 1 shows relation of unaliased image, aliasing image and folded image in a pixel. To calculate unaliased image of channel i, data of channel j ($$$i \neq j$$$) was used. By using phase of each image and absolute value of folded image, unaliased image was decomposed as equation 2. $$S_i=\begin{vmatrix}R\end{vmatrix}\begin{vmatrix}\frac{sin(\psi^{i+j}-\phi^{i+j})sin(\theta^{i+j}-\theta^j)}{sin(\theta^j-\phi^{i+j})sin(\theta^i-\theta^j)}\end{vmatrix}e^{i\theta^i}\ \ (2)$$ Where $$$R=R_i+R_je^{i\alpha_j}$$$ is sum of folded image of channel i and j, $$$R_{i,j}$$$ is folded image of channel i and j, $$$\theta^{i+j}, \phi^{i+j}, \psi^{i+j}$$$ are phase of sum of channel i and j of unaliased, aliasing, and folded image, and $$$\alpha_j$$$ is determined to minimize enhancement of noise as follows. In this study, noise of $$$R_i$$$ and $$$R_j$$$ were considered. By using propagation law of error, noise of decomposed unaliased image was estimated as equation 3, and $$$\alpha_j$$$ was determined as minimizing equation 3. $$(\delta S_i)^2=(\frac{\partial S_i}{\partial R_i})^2(\delta R_i)^2+(\frac{\partial S_i}{\partial R_j})^2(\delta R_j)^2=\frac{2sin^2(\theta^{i+j}-\theta^j)}{sin^2(\theta^{i+j}-\phi^{i+j})sin^2(\theta^i-\theta^j)}(\delta R)^2\ \ (3)$$ Where $$$\delta R_{i,j}$$$ are noise of $$$R_{i,j}$$$ . For simplicity, $$$\delta R_i=\delta R_j=\delta R$$$ was assumed. $$$\theta^{i+j},\ \phi^{i+j},$$$ and $$$\theta^j$$$ depend on $$$\alpha_j$$$ . This calculation was done for each pixel and each channel, and unaliased image of each channel was calculated.
iii) Combining multi channel data
In the region of edge between brain and air, phase estimation was not accurate and unfolding procedure described above failed, so conventional parallel imaging was applied in such region. In other regions, sensitivity map was used as equation 4. $$ I(x,y) = \frac{\sum_{i=1}^{Ch} c_i^*(x,y) S_i(x,y)}{\sum_{i=1}^{Ch} \begin{vmatrix}c_i(x,y)\end{vmatrix}^2}\ \ (4)$$ Where I(x,y) is combined signal, Ch is number of receiver channels, and $$$c_i(x,y)$$$ is coil sensitivity of channel i.
Experiment
Experiment was conducted on 3 Tesla whole body MRI system (Hitachi, Ltd.). A healthy volunteer was imaged. This study was approved by the ethics committee of Hitachi group headquarters. 15 channel receiving coil was used. Scan parameter of T2 weighted image was follows; TR / TE = 4500 msec / 90 msec, Freq# x Phase# = 256 x 256, slice# = 22, echo train length = 14, scan time = 1 min 25 sec. Full sampled image was acquired and under sampling was applied retrospectively. Acceleration factor was 3.
Evaluation
SNR of white matter was compared between full sampled image, conventional parallel imaging, and proposed method.
Results and Discussions
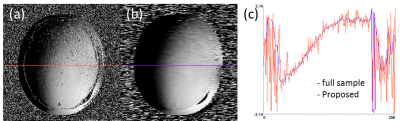
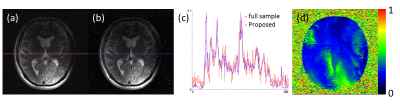
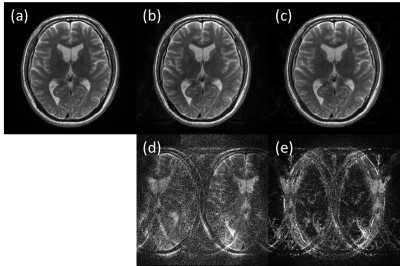
Figure 2 shows phase distribution of full sample, and estimated using ACS data of a channel. By using central 64 lines of k-space, accurate phase distribution was measured. Figure 3 shows full sampled and unfold image of a channel. Line profile of horizontal line is also shown. Line profile is smoother in proposed method than full sample, because noise enhancement is mitigated as shown in figure 3 (d). Figure 4 shows T2 weighted images; (a): full sample, (b): conventional parallel imaging, and (c): proposed method. Figure 4 (d) and (e) shows difference of (a) and (b), and (a) and (c). In proposed method, difference was smaller than conventional parallel imaging. In table 1, SNR of white matter is summarized. In proposed method, SNR was higher than that of conventional parallel imaging.Conclusions
A new algorithm of parallel imaging reconstruction for FSE sequence using phase distribution was proposed. By minimizing enhancement of noise, higher SNR was achieved.Acknowledgements
No acknowledgement found.References
1. Klaas P. Pruessmann, et al. SENSE: Sensitivity Encoding for Fast MRI. MRM 42: 952-962 (1999)
2. Daniel K. Sodickson, et al. Simultaneous Acquisition of Spatial Harmonics (SMASH): Fast Imaging with Radiofrequency Coil Arrays. MRM 38: 591-603 (1997)
3. Mark A. Griswold, et al. Generalized autocalibrationg partially parallel acquisitions (GRAPPA). MRM 47: 1202-1210 (2002)
4. Felix A. Breuer, et al. Controlled Aliasing in Volumetric Parallel Imaging (2D CAIPIRINGA). MRM 55: 549-556 (2006)
5. Martin Blaimer, et al. Comparison of Phase-Constrained Parallel MRI Approaches: Analogies and Differences. MRM 75: 1086-1099 (2016)
Figures