3510
Accelerated reconstruction for calibrationless parallel imaging using grouped joint nonlinear inversion and its application in myelin water imaging1Center for Brain Imaging Science and Technology, Department of Biomedical Engineering, Zhejiang University, Hangzhou, China, 2MR Collaboration NE Asia, Siemens Healthcare, Shanghai, China, 3Department of Imaging Sciences, University of Rochester, Rochester, NY, United States
Synopsis
The simultaneous estimation of images and coil sensitivities using joint nonlinear inversion (JNLINV) has been shown to be effective for
Introduction
The joint estimation of images and coil sensitivities from undersampled k-space data using nonlinear inversion is recently proposed and demonstrates that no calibration is required for multi-echo and multi-contrast parallel imaging acquisition. This joint nonlinear inversion (JNLINV) method [1], derived from the previously proposed NLINV approach [2], takes advantage of the fact that coil sensitivities are independent of echoes or contrasts and achieves one-sixth RMSE of that with NLINV. This calibrationless method has been successfully applied for accelerating many protocols with a negligible RMSE, including multi-echo, phase-cycled bSSFP sequences, and some multi-contrast protocols [1].
This study proposes a grouped JNLINV (gJNLINV) method that achieves about a 3-fold reduction in reconstruction time with a similar RMSE as JNLINV for the multi-echo data with a long echo train. We also demonstrate the application of this method for myelin water imaging using multi-echo GRE data.
Theory
Under-sampled data $$$y$$$ from the images $$$\rho$$$ with coil sensitivities $$$c$$$ and k-space sampling pattern $$$P$$$ are represented by $$$y=PF(c\rho)$$$, where $$$F$$$ is the Fourier transform. It is simplified as a nonlinear operation $$$y=N(x)$$$ in the JNLINV method. The unknown $$$x$$$ contains both images and coil sensitivities: $$$x=[\rho,c]$$$, and can be computed by solving the update steps $$$dx=[d\rho,dc]$$$ using a linear approximation through the Jacobian $$$D$$$ (or the Fréchet derivative) [2] at the $$$n$$$th update step of $$$x$$$ with coil terms and an $$$l_{2,1}$$$ norm of image gradients as the penalty terms:
$$min_{dx}||DN(x^n)dx+N(x^n)-y||_2^2+\alpha^n||W(c^n+dc)||_2^2+\beta^n||\nabla(\rho^n+d\rho)||_{2,1}\qquad\qquad(1)$$
where $$$n$$$ is the index of the current update step, $$$W$$$ is a low-pass filter for smoothing the coil sensitivities, $$$\nabla$$$ is a spatial gradient operator, and $$$\alpha$$$, $$$\beta$$$ are coefficients of penalties and are reduced 2-fold in each outer iteration of the $$$dx$$$ updates.
For the under-sampled multi-echo data with a large echo train (e.g., 32 echoes or more), the direct application of the standard JNLINV is time consuming due to the substantial number of unknowns. We propose the gJNLINV to accelerate the reconstruction of all the echoes:
(i) Apply JNLINV to the first few echoes for coil sensitivities;
(ii) Divide the remaining echoes into groups which are processed using parallel computation to save reconstruction time. The coil sensitivities obtained from step (i) are subsequently applied in the operation $$$N$$$, and the coil terms are removed from both $$$x$$$ and Eq. (1), i.e., $$$x=[\rho]$$$, and the objective function for the $$$dx$$$ optimization becomes:
$$min_{dx}||DN(x^n)dx+N(x^n)-y||_2^2+\beta^n||\nabla(\rho^n+d\rho)||_{2,1}$$
Methods
The multi-echo GRE data were acquired on a 3T MAGNETOM Prisma (Siemens Healthcare, Erlangen, Germany) using 16-head elements of a 20-channel head-neck coil. The sequence parameters were as follows: 32 echoes, TE = 2.7 : 1.5 : 49.2 ms, TR = 62 ms, voxel size = 0.94 × 0.94 × 2 mm3, and acquisition matrix = 256 × 256 × 64.
Reconstruction was performed on a server (Xeon E5-2680, 256 GB memory) with MATLAB R2014a. All 32 echo images were evenly divided into eight echo groups (i.e., four echoes in each group) and were manually 2 × 2 under-sampled. Echoes 1 to 4 were processed using JNLINV for coil sensitivities, and the remaining echo groups were reconstructed using the gJNLINV through parallel computing. $$$\alpha^0=0.05$$$, $$$\beta^0=0.1$$$.
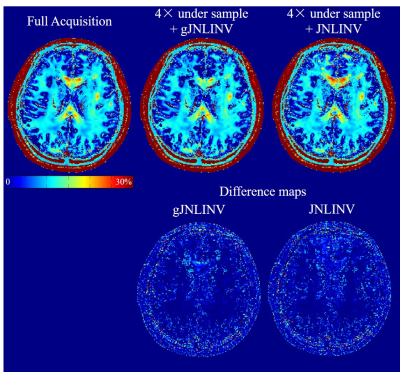
Myelin water fraction (MWF) maps were calculated from all the reconstructed images with 32 TEs. The data was fitted to a three-pool model [3]:
$$s(TE)=A_{my}e^{-TE/T_{2,my}^*}+A_{ma}e^{-TE/T_{2,ma}^*}+A_{mx}e^{-TE/T_{2,mx}^*}$$
where $$$A$$$ is the signal amplitude of each component ($$$my$$$: myelin, $$$ma$$$: axon, $$$mx$$$: mixed pool). The MWF was calculated as $$$MWF=A_{my}/(A_{my}+A_{ma}+A_{mx})$$$
Results
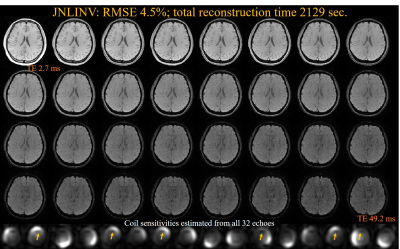
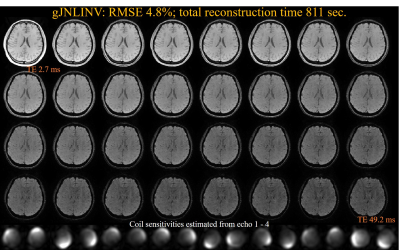
The reconstructed 32-echo images for a single slice using JNLINV and gJNLINV, together with their RMSEs compared with the fully sample data and the reconstruction time, are demonstrated in Figs. 1 and 2, respectively. The total reconstruction time for the gJNLINV (811 sec) comprises two parts: the first 4 echoes (389 sec) and the remaining 28 echoes using parallel computing (422 sec); the time cost of applying JNLINV to all 32 echoes was 2129 sec. Both methods achieved similar low RMSE (standard 4.5% vs. proposed 4.8%). The MWF maps and their comparisons are shown in Fig. 3.Discussion and Conclusion
The gJNLINV method uses only about one-third of the computation time for reconstructing all 32 echoes compared with JNLINV. It reduces the number of unknowns in each optimization procedure and enables parallel computation for accelerated reconstruction. Besides having a nearly identical low RMSE to JNLINV, gJNLINV also produces coil maps with higher fidelity as it avoids the discontinuities in the estimated coil sensitivities (yellow arrows in Fig. 1). The MWF maps from the reconstructed 4× under-sampled images using both methods are in good agreement with those from the fully acquired data. The gJNLINV method is also likely applicable to the fast calibrationless reconstruction of other multi-echo sequences, e.g., CPMG [4], GRASE [5].Acknowledgements
This work was supported by the National Key R&D Program of China (2017YFC0909200), National Natural Science Foundation of China (81401473, 91632109, 81371518) and the Fundamental Research Funds for the Central Universities (2017QNA5016).References
1. Bilgic B, Zhao B, Chatnuntawech I, Wald LL, Setsompop K. Calibrationless Parallel Imaging in Multi Echo/Contrast Data. Proc. Intl. Soc. Mag. Reson. Med. 2017;25:139.
2. Uecker M, Hohage T, Block KT, Frahm J. Image reconstruction by regularized nonlinear inversion--joint estimation of coil sensitivities and image content. Magn. Reson. Med. 2008;60:674–82.
3. Lancaster JL., Andrews T, Hardies LJ, Dodd S, Fox PT. Three-pool model of white matter. J. Magn. Reson. Imaging. 2003;17:1–10.
4. Whittall KP, Mackay AL, Graeb DA, Nugent RA, Li DKB, Paty DW. In vivo measurement of T2 distributions and water contents in normal human brain. Magn. Reson. Med. 1997;37:34–43.
5. Prasloski T, Rauscher A, MacKay AL, Hodgson M, Vavasour IM, Laule C, Madler B. Rapid whole cerebrum myelin water imaging using a 3D GRASE sequence. Neuroimage. 2012;63:533–539.
Figures