3508
A Method for Automatically Determining an Optimal Kernel Size in ESPIRiT Reconstruction1Imaging Physics Department, The University of Texas MD Anderson Cancer Center, Houston, TX, United States, 2Diagnostic Radiology Department, The University of Texas MD Anderson Cancer Center, Houston, TX, United States, 3GE Healthcare Technologies, Waukesha, WI, United States
Synopsis
ESPIRiT is a hybrid-domain parallel imaging method which can estimate the coil-sensitivity information from the k-space calibration matrix. In ESPIRiT, the calibration matrix is constructed by sliding a window through the fully sampled data region of auto-calibrating signals. Presently, the kernel size of the sliding window determining the performance of ESPIRiT reconstruction is empirically chosen, even though an optimal value may vary depending on a combination of scan parameters and scan configurations. In this work, we developed an automatic data-driven method for determining an optimal kernel size in ESPIRiT to reduce the performance variation of ESPIRiT reconstructions.
INTRODUCTION
ESPIRiT is a hybrid-domain parallel imaging method that has the combined advantages of SENSE (which requires explicit coil sensitivities) and GRAPPA (which is based on local kernels in k-space that encode the coil sensitivities).1-3 In ESPIRiT, a coil calibration matrix is constructed by sliding a window through the fully sampled data region of auto-calibrating signals (ACS). The calibration matrix intrinsically has a null space and the k-space local kernels can be determined from the vectors supporting the null space.1 The accuracy in determining the calibration matrix and k-space local kernels, and therefore the ultimate performance of ESPIRiT reconstruction may be dependent on the kernel size of the sliding window. Presently, the actual kernel size used is empirically chosen, even though an optimal value may vary depending on a combination of various scan parameters and scan configurations. In this work, we developed an automatic data-driven method for determining an optimal kernel size of the sliding window in ESPIRiT.
METHODS
In ESPIRiT, the kernel size of the sliding window used in determining the calibration matrix is selected empirically and fixed independent of scan parameters and scan configurations.1 Once selected, the kernel size determines the number of the weighting coefficients that are used for k-space calibration (NKernel∙NKernel∙NCoil), and the number of equations that can be composed for calculating the weighting coefficients (ACSkx−NKernel+1)∙(ACSky−NKernel+1) where ACSkx and ACSky are the numbers of ACS lines in kx and ky, NKernel is the kernel size, and NCoil is the number of coils. Increasing the kernel size helps to estimate the calibration matrix by including more neighbors in k-space and increasing the number of weighting coefficients. On the other hand, fewer number of composed equations becomes available, which limits training accuracy in the required Singular-Value Decomposition (SVD) process.
In the proposed method for determining an optimal kernel size, we first determine a series of calibration matrices with different kernel sizes. We then subsample the fully sampled ACS data regions using the same subsampling factor(R) and pattern that are used in acquiring the outer k-space regions. The missing k-space lines in the ACS region are reconstructed according to the ESPIRiT algorithm using the calibration matrix from each kernel size. These reconstructed k-space lines in the ACS region are compared with the actually acquired k-space lines to help select an optimal kernel size. In our method, a simple k-space mean squared error (kMSE) was used as the quality index in selecting the kernel size. The final images were reconstructed using the calibration matrix with the selected kernel size and the Cartesian conjugate gradient ESPIRiT.4
We evaluated the proposed method with in vivo axial abdomen images that were acquired using 31 channels of a body array coil on a 3.0T whole-body wide bore scanner (GE Healthcare, Waukesha, Wisconsin, USA). Fully sampled k-space data were acquired using a dual-echo FLEX pulse sequence with the following scan parameters: TR/TE1/TE2=4056/1180/2380 us, NFE/NPE=256/130, FOV=50x40 cm, RBW=±142.86 kHz, NSlice=112, slice-thickness/slice-gap=4/-2 mm, and scan-time=22 secs. The proposed algorithm was implemented in MATLAB (MathWorks, Natick, Massachusetts, USA) and an in-phase echo image was selected from a slice, then decimated in k-space to simulate subsampled k-space data (R=2, ACSkx=256, and ACSky=24).
RESULTS
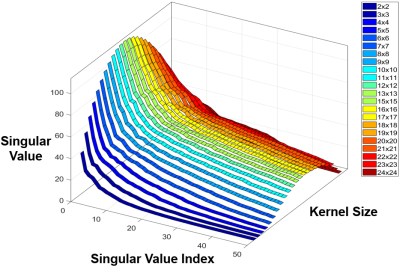
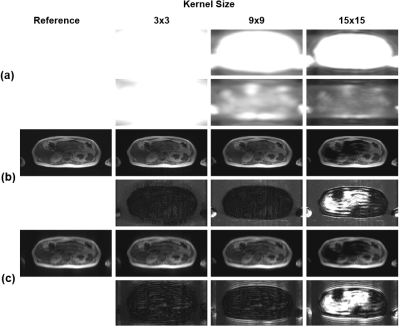
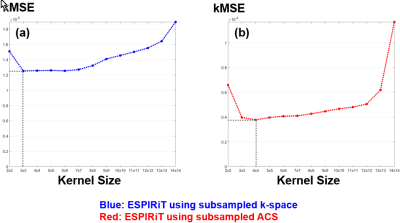
Fig. 1 and Fig. 2(a) show the results of SVD coil-correlation estimation and Eigen-Value Decomposition (EVD) coil-sensitivity estimation for a range of the different kernel sizes. Clearly, both SVD and EVD estimations are dependent on the kernel size selected. The effect of the kernel size on the fidelity of the ESPIRiT reconstructed images using the fully sampled image as the reference is shown in Fig. 2(b) and Fig. 3(a). The proposed method was able to find an optimal kernel size of “4x4” (Fig. 2(c) and Fig. 3(b)), which is next to the optimal kernel size of “3x3” when the subsampled entire k-space was used (Fig. 3). The kMSE difference between the two kernel sizes was only 4.79x10-8. It is noted that the small optimal kernel size of 3x3 was related to the small number of phase-encoding lines (NPE=130) used in our testing.DISCUSSION
The kernel size in the original ESPIRiT is pre-selected empirically and fixed. In principle, many scan parameters and configurations could affect the optimal kernel size, including subsampling factor, the number of receiver coils and their geometric factors, the number of k-space encoding, the size of additionally acquired ACS lines, and signal-to-noise conditions. The method proposed here does not require any change in the acquisition and is data-driven. Therefore, we expect to reduce the performance variation of ESPIRiT when different scan parameters and scan configurations are used.Acknowledgements
Part of the research was conducted at the Center for Advanced Biomedical Imaging at The University of Texas MD Anderson Cancer Center with equipment support from GE Healthcare.References
1. Uecker M, Lai P, Murphy MJ, Virtue P, Elad M, Pauly JM, Vasanawala SS, and Lustig M. ESPIRiT - An Eigenvalue Approach to Autocalibrating Parallel MRI: Where SENSE meets GRAPPA. Magn Reson Med. 2014;71(3):990-1001.
2. Pruessmann KP, Weiger M, Scheidegger MB, and Boesiger P. SENSE: Sensitivity encoding for fast MRI. Magn Reson Mad. 1999;42:952-962.
3. Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, and Hasse A. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn Reson Med. 2002;47:1202-1210.
4. Uecker M, Virtue P, Vasanawala SS, and Lustig M. ESPIRiT Reconstruction Using Soft SENSE. Proc Intl Soc Mag Reson Med. 2013:127.
Figures