3505
Improving Parallel Imaging by Jointly Reconstructing Multi-Contrast Data1Martinos Center for Biomedical Imaging, Charlestown, MA, United States, 2Department of Electrical Engineering, University of Southern California, Los Angeles, CA, United States
Synopsis
We propose a general joint reconstruction framework to accelerate multi-contrast acquisitions further than currently possible with conventional parallel imaging. Our joint parallel imaging techniques simultaneously exploit similarities between echoes/phase-cycles/contrasts, virtual coil concept, partial Fourier acquisition, complementary sampling across images along with limited support and smooth phase constraints. These permit highly accelerated 2D, Simultaneous MultiSlice and 3D acquisitions as well as improved calibrationless parallel imaging from multiple contrasts. Our algorithms, JVC-GRAPPA and J-LORAKS, provide over 2-fold improvement in reconstruction error compared to conventional GRAPPA, with improved mitigation of artifacts and noise amplification.
Introduction
MRI exams routinely involve multi-contrast acquisition to obtain complementary information. Multi-echo acquisition finds applications in relaxation time mapping [1-3] and water/fat imaging [4-7]. Phase-cycled bSSFP requires multiple images with different phase offsets to shift the location of B0-related artifacts. These images are then combined to eliminate banding artifacts [8-10]. Unfortunately, high-resolution multi-contrast/echo/cycle imaging with whole-brain coverage leads to excessive scan times.
For faster acquisitions, previous joint reconstruction techniques explored k-space interpolation across time [11-12], echoes [13-14], or excitation modes [15]. Herein, we propose a general framework to accelerate multi-contrast acquisitions further than currently possible. We introduce Joint Virtual Coil (JVC-) GRAPPA, which allows all coils from all contrasts to contribute to reconstruction of a particular channel. This employs VC concept [16-18] and complementary k-space sampling across contrasts.
We extend joint parallel imaging to exploit limited support and smooth phase constraints [19-21] through Joint (J-) LORAKS. J-LORAKS achieves a more parsimonious low rank representation in k-space by considering multi-contrast images as additional coils. It seamlessly incorporates partial Fourier (PF) and permits improved calibrationless reconstruction.
Matlab code/data: http://bit.ly/2sY1FJT
Reconstruction Algorithms
All experiments used 16 SVD compressed channels [22-23] and were performed at 3T. PF experiments employed POCS processing [24-26] following GRAPPA reconstruction [27].
JVC-GRAPPA: creates additional channels by treating data from other contrasts as extra coils. To increase size of available k-space for calibration of large number of kernels, an initial Joint-GRAPPA was performed from ACS data. VC concept was then employed to double the number of channels. This way, the entire k-space of the interim reconstruction became available for calibration. We run 3 iterations to refine the reconstruction.
J-LORAKS: also stacks data from all contrasts in the channel axis, and employs VC. It enforces local k-space neighborhoods, now extended across contrasts, to have low rank. The parameters associated with this constraint, neighborhood size and rank of local k-space matrices, were optimized to reduce RMSE.
Data Acquisition and Comparison Cases
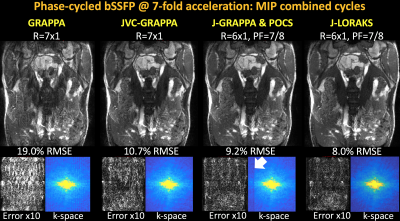
2D Phase-Cycled bSSFP: was acquired with four phase-cycles, FOV=380×380mm2, matrix=160×160, TR/TE=3.3/1.54ms, using 34-channel reception and 20 ACS lines.
GRAPPA and JVC-GRAPPA were performed at R=7x1 undersampling. Keeping the net acceleration the same, R=6x1-fold undersampling with 7/8 PF was explored using J-GRAPPA & POCS and J-LORAKS.
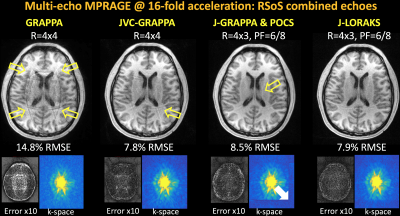
3D ME-MPRAGE: was collected at 1mm3, FOV=256×240×192mm3, TR/TI=2530/1100ms, TE’s=1.7/3.6/5.4/7.3ms, 32-channel reception and 24x24 ACS region.
GRAPPA and JVC-GRAPPA were performed with R=4x4 undersampling. At the same acceleration, R=4x3 with 6/8 PF was explored using J-GRAPPA & POCS, as well as J-LORAKS.
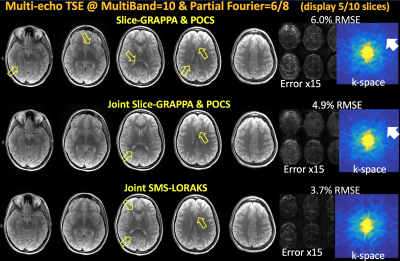
SMS ME-TSE: was acquired using FOV=240×240, matrix=256×256, slice gap=12.8mm, TR=4sec, TE’s=12/25/50/62/87/99ms, 32-channel reception and 24 ACS lines.
Slice-GRAPPA & POCS was employed at MultiBand-10 acceleration with 6/8 PF. Joint reconstructions were performed with Joint Slice-GRAPPA & POCS and J-SMS-LORAKS.
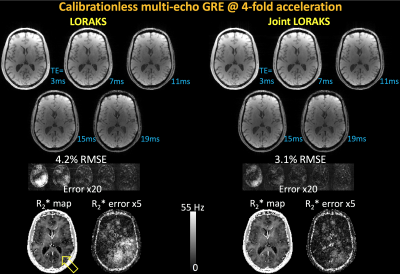
Calibrationless 3D ME-GRE: was collected with FOV=240×240×192, matrix=160×160×128, TR=23 ms, TE’s=3/7/11/15/19ms using 32-channel reception. R=4-fold calibrationless Poisson sampling was utilized.
Results
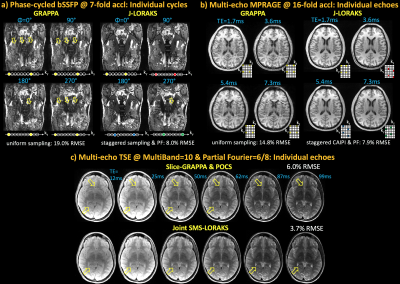
bSSFP [Fig1]: GRAPPA broke down with 19.0% RMSE, while JVC-GRAPPA demonstrated better artifact mitigation with 10.7% error. POCS completed k-space appeared underestimated in J-GRAPPA with PF. J-LORAKS mitigated this problem with the best RMSE (8.0%).
ME-MPRAGE [Fig2]: GRAPPA demonstrated severe artifacts with 14.8% RMSE. JVC-GRAPPA partially mitigated these with 7.8% error. Although J-GRAPPA & POCS further reduced artifacts, partially sampled k-space suffered from underestimation. J-LORAKS addressed these to provide a cleaner reconstruction (7.9% RMSE).
ME-TSE [Fig3]: Slice-GRAPPA followed by POCS returned 6.0% error. Despite the reduction in RMSE to 4.9%, some artifacts were present in Joint Slice-GRAPPA. J-SMS-LORAKS attained the best RMSE (3.7%), with some residual artifacts.
Calibrationless ME-GRE [Fig4]: J-LORAKS mitigated the high error in early echoes of conventional LORAKS, and alleviated the underestimation in the R2* map.
[Fig5]: Compares individual cycles/contrasts.
Discussion and Conclusion
Proposed joint reconstruction algorithms provided up to 2.4-fold reduction in RMSE over conventional parallel imaging. This was made possible by exploiting similarities between multi-contrast images, complementary sampling and VC concept. JVC-GRAPPA converted intensity and phase differences into extra spatial encoding, while J-LORAKS achieved lower rank k-space matrices due to added redundancy from multiple images. J-LORAKS also allowed improved calibrationless reconstruction and flexible PF sampling.
A drawback of joint reconstruction is the increased computation time. For Fig2, GRAPPA took 6sec, while JVC-GRAPPA and J-LORAKS required 6.8min and 5.4min. This can be mitigated by more coil compression achieved through e.g. GCC [28], restricting calibration to a smaller portion of k-space in JVC-GRAPPA, and reducing J-LORAKS iterations (currently 100).
Another limitation is motion between scans. While this will not affect multi-echo acquisitions, phase-cycled bSSFP could be impacted by potential mismatches. JVC-GRAPPA employs low-resolution kernels, and maybe resilient against small amounts of motion. For larger mismatches, an initial GRAPPA could enable motion correction, followed by JVC-GRAPPA or J-LORAKS reconstruction.
Acknowledgements
We acknowledge grant support from NIH NINDS grant number R24 MH10609603 and NIBIB R01 EB02061302, R01 EB019437, P41 EB015896 and R21 EB02295102.References
1. Ben‐Eliezer N, Sodickson D, Block K. Rapid and accurate T2 mapping from multi–spin‐echo data using Bloch‐simulation‐based reconstruction. Magn. Reson. Med. 2015;73.2:809–817.
2. Sumpf T, Uecker M, Boretius S, Frahm J. Model‐based nonlinear inverse reconstruction for T2 mapping using highly undersampled spin‐echo MRI. J. Magn. Reson. Imaging 2011;34.2:420–428.
3. Wu B, Li W, Avram AV, Gho S-M, Liu C. Fast and tissue-optimized mapping of magnetic susceptibility and T2* with multi-echo and multi-shot spirals. Neuroimage 2012;59:297–305. doi: 10.1016/j.neuroimage.2011.07.019.
4. Reeder S, McKenzie C, Pineda A, Yu H, Shimakawa A, Brau AC, Hargreaves BA, Gold GE, Brittain JH. Water–fat separation with IDEAL gradient‐echo imaging. J. Magn. Reson. Imaging 2007;25.3:644–652.
5. Yu H, McKenzie C, Shimakawa A, Vu A, Brau AC, Beatty P, Pineda A, Brittain JH, Reeder S. Multiecho reconstruction for simultaneous water‐fat decomposition and T2* estimation. J. Magn. Reson. Imaging 2007;26.4:1153–1161.
6. Glover G. Multipoint Dixon technique for water and fat proton and susceptibility imaging. J. Magn. Reson. Imaging 1991;1.5:521–530.
7. Dixon W. Simple proton spectroscopic imaging. Radiology 1984;153.1:189–194.
8. Miller KL, Smith SM, Jezzard P, Pauly JM. High-resolution FMRI at 1.5T using balanced SSFP. Magn. Reson. Med. 2006;55:161–170. doi: 10.1002/mrm.20753.
9. Lee J, Dumoulin S, Saritas E, Glover G, Wandell B, Nishimura D, Pauly J. Full‐brain coverage and high‐resolution imaging capabilities of passband b‐SSFP fMRI at 3T. Magn. Reson. Med. 2008;59.5:1099–1110.
10. Çukur T, Lustig M, Nishimura DG. Multiple-profile homogeneous image combination: Application to phase-cycled SSFP and multicoil imaging. Magn. Reson. Med. 2008;60:732–738. doi: 10.1002/mrm.21720.
11. Huang F, Akao J, Vijayakumar S, Duensing GR, Limkeman M. k-t GRAPPA: A k-space implementation for dynamic MRI with high reduction factor. Magn. Reson. Med. 2005;54:1172–1184. doi: 10.1002/mrm.20641.
12. Jung B, Ullmann P, Honal M, Bauer S, Hennig J, Markl M. Parallel MRI with extended and averaged GRAPPA kernels (PEAK‐GRAPPA): Optimized spatiotemporal dynamic imaging. J. Magn. Reson. Imaging 2008;28:1226–1232.
13. Kim H, Kim D-H, Sohn C-H, Park J. Rapid chemical shift encoding with single-acquisition single-slab 3D GRASE. Magn. Reson. Med. 2017. doi: 10.1002/mrm.26595.
14. Chen F, Shi X, Chen S, Johnson E, Chen B. Accelerated model-based proton resonance frequency shift temperature mapping using echo-based GRAPPA reconstruction. Magn. Reson. Imaging 2015;33.2:240–245.
15. Orzada S, Maderwald S, Poser B, Bitz AK, Quick HH, Ladd ME. RF excitation using time interleaved acquisition of modes (TIAMO) to address B1 inhomogeneity in high-field MRI. Magn. Reson. Med. 2010;64:327–333. doi: 10.1002/mrm.22527.
16. Blaimer M, Jakob P, Breuer F. Regularization method for phase‐constrained parallel MRI. Magn. Reson. Med. 2014;72.1:166–171
17. Blaimer M, Gutberlet M, Kellman P, Breuer F, Kostler H, Griswold MA. Virtual coil concept for improved parallel MRI employing conjugate symmetric signals. Magn. Reson. Med. 2009;61:93–102.
18. Blaimer M, Choli M, Jakob P, Griswold MA, Breuer FA. Multiband phase‐constrained parallel MRI. Magn. Reson. Med. 2013;69:974–980.
19. Haldar JP. Low-Rank Modeling of Local k-Space Neighborhoods (LORAKS) for Constrained MRI. IEEE Trans. Med. Imaging 2014;33:668–681. doi: 10.1109/TMI.2013.2293974.
20. Haldar JP, Zhuo J. P-LORAKS: Low-rank modeling of local k-space neighborhoods with parallel imaging data. Magn. Reson. Med. 2016;75:1499–1514. doi: 10.1002/mrm.25717.
21. Haldar JP. Autocalibrated loraks for fast constrained MRI reconstruction. In: 2015 IEEE 12th International Symposium on Biomedical Imaging (ISBI). IEEE; 2015. pp. 910–913. doi: 10.1109/ISBI.2015.7164018.
22. Huang F, Vijayakumar S, Li Y, Hertel S, Duensing GR. A software channel compression technique for faster reconstruction with many channels. Magn. Reson. Imaging 2008;26:133–141. doi: 10.1016/j.mri.2007.04.010.
23. Buehrer M, Pruessmann KP, Boesiger P, Kozerke S. Array compression for MRI with large coil arrays. Magn. Reson. Med. 2007;57:1131–1139. doi: 10.1002/mrm.21237.
24. Liang Z, Lauterbur P. Principles of magnetic resonance imaging: a signal processing perspective. SPIE Optical Engineering Press; 2000.
25. Haacke E, Lindskogj E, Lin W. A fast, iterative, partial-Fourier technique capable of local phase recovery. J. Magn. Reson. 1991.
26. Cuppen J, Est A van. Reducing MR imaging time by one-sided reconstruction. Magn. Reson. Imaging 1987;5.6:526–527.
27. Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn. Reson. Med. 2002;47:1202–1210. doi: 10.1002/mrm.10171.
28. Zhang T, Pauly JM, Vasanawala SS, Lustig M. Coil compression for accelerated imaging with Cartesian sampling. Magn. Reson. Med. 2013;69:571–582. doi: 10.1002/mrm.24267.
Figures