3415
An image-based method for undistorted image estimation from distorted brain EPI image with field inhomogeneity1Hokkaido University of Science, Sapporo, Japan, 2Kagoshima University, Kagoshima, Japan
Synopsis
Our purpose was to develop an image-based method for undistorted image estimation from the distorted EPI image using T1 weighted image. Our basic idea to estimate the field inhomogeneity map is to reproduce the distorted EPI image, and estimates the undistorted image using the estimated field inhomogeneity map based on the signal equation in a single-shot EPI k-space trajectory. The value of the NRMSE between the measured EPI and synthesized EPI was 0.017, and both images were in good agreement. Results demonstrate that our proposed method was able to perform a reasonable estimation of the field inhomogeneity map and undistorted EPI image.
INTRODUCTION
Magnetic field inhomogeneities caused by susceptibility differences result in significant geometric distortion in single-shot echo planar imaging (EPI) images. Many methods have been proposed for correcting the distortion in EPI. Among the distortion correction methods, the most commonly used method is the field-map-based approach, which requires additional acquisition to obtain the field map1 and has the problem of registering the field map to the EPI image.2 As an alternative approach, non-rigid registration methods have been proposed, which register the distorted EPI image into an undistorted reference image. However, it is known that the deformations are described by many parameters to control the geometric transformation, and the accuracy of such methods depends on how the deformations are constrained. In this study, our purpose was to develop an image-based method for undistorted image estimation from the distorted EPI image using T1 weighted image (T1WI) based on MR imaging physics.METHODS
We propose the iterative-method to estimate an undistorted image and its associated field inhomogeneity map using conjugate gradient algorithm. Our basic idea to estimate the field inhomogeneity map in EPI is to reproduce the distorted EPI image based on the signal equation in a single-shot EPI k-space trajectory. To synthesize the distorted EPI image, we make use of the image-based method3 which can reduce the computation time compared to the k-space texture method4. The MR signal in synthesized EPI was calculated on a voxel-by-voxel basis using the estimated T2 value and field inhomogeneity ΔB by the following equation:
$$I(x,y,T2, \Delta B)=\sum_{u=0}^{M-1} \sum_{v=0}^{N-1} A(u,v)\cdot exp(-\frac{TEeff}{T2(u,v)})\cdot sinc (\pi (x-u-\frac{\Delta B(u,v)}{\Delta x \cdot Gx})) \cdot sinc (\pi (y-v-\frac{\Delta B(u,v)}{\Delta y \cdot Gy}))$$
where Δx and Δy are pixel spacing in x and y direction, respectively. Gx is the gradient in the x direction, and Gy = Gbτ /Δty (Gb is the average blip gradient in the y direction during the duration τ, and Δty is the time intervals between adjacent points in the phase-encoding directions in k-space). To estimate T2 value and ΔB at each point, we defined the cost function using the synthesized EPI image and the measured EPI image with geometric distortion as follows.
$$J(T2, \Delta B) = \sum_{x=0}^{M-1}\sum_{y=0}^{N-1}|Y(x,y)-I(x,y,T2, \Delta B) |^2 +\beta_1 R_1(\Delta B)+\beta_2 R_2 (T2)$$
where Y(x,y) is the measured EPI image, R1(ΔB(x,y)) and R2(T2(x,y)) are regularization terms. To result in a relatively smooth field inhomogeneity map, R1(ΔB(x,y)) penalizes the roughness of the estimated field inhomogeneity map. To obtain the structural information in the distorted area in the measured EPI image, we used the same slice of the T1WI as the measured EPI image. We generated the initial estimated T2map by applying the gray-scale inversion and histogram specification5 to the T1WI. We used Tikhonov regularization for R2(T2(x,y)), the initial estimated T2map was used as the reference image in Tikhonov regularization. The estimation of T2 and ΔB maps was performed to minimize the cost function using an iterative conjugate gradient algorithm. The spin echo (SE) EPI and T1WI data of a healthy volunteer were acquired using a 1.5-tesla clinical Siemens scanner. The SE EPI data was obtained by a single-shot EPI pulse sequence (FOV: 230 mm, TR=8600ms, TE=119ms, 128×128 in-plane resolution, 3 mm thickness). Three dimensional T1WI covering the same area in EPI was obtained by MPRAGE sequence (FOV: 230 mm, TR=2090ms, TE=3.93ms, TI=1100ms, FA=15°, 256×256 in-plane resolution, 1 mm thickness). To evaluate the performance of our methods, we used the normalized root mean square error (NRMSE) between the measured EPI and synthesized EPI.
RESULTS and DISCUSSION
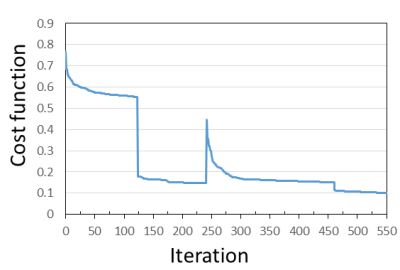
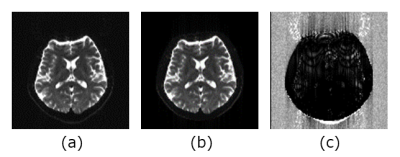
Figure 1 shows the estimation process in our method and illustrates the convergence of the cost function over iteration. The computation time was 18938.7 sec. Figure 2(a), (b) and (c) shows the measured EPI image, the synthesized EPI image and the absolute difference image between them. The value of the NRMSE was 0.017. These results demonstrate that both images were in good agreement. Figure 3(a), (b), (c) and (d) shows T1WI, initial T2map, estimated undistorted EPI image, and estimated ΔB map. As shown in Fig.3(c), geometric distortion in the frontal lobe of the brain, where the field inhomogeneity was high in Fig.3(d), was reduced significantly by proposed method.CONCLUSION
We have presented an image-based method for undistorted image estimation from the distorted EPI image using T1WI based on MR imaging physics. Our results demonstrate that our proposed method was able to perform a reasonable estimation of the field inhomogeneity map and undistorted EPI image.Acknowledgements
This work was supported by Japan Society for the Promotion of Science (JSPS) KAKENHI Grant Number 15K08695 and 26293278.References
1. Jezzard P, Balaban RS. 1995. Correction for geometric distortion in echo planar images from B0 field variations. Magn Reson Med 34:65-73.
2. Sutton BP, Noll DC, Fessler JA, 2004. Dynamic field map estimation using a spiral-in/spiral-out acquisition. Magn Reson Med. 51:1194-1204.
3. Kumazawa S, Yoshiura T, Kikuchi A, et al. 2017. An improved image-based method for field inhomogeneity map in distorted brain EPI image. Proc ISMRM, 1526.
4. Kumazawa S, Yoshiura T, Honda H. 2015. Image-based estimation method for field inhomogeneity in brain echo-planar images with geometric distortion using k-space textures. Concept Magn Reson B. 45:142-152.
5. Coltuc D, Bolon P, Chassery JM. 2006. Exact histogram specification. IEEE Trans Image Process. 15:1143-1152.
Figures